There are still a few more things I want to say about the 600-cell. Last time I described the ‘compound of five 24-cells’. David Richter built a model of this, projected from 4 dimensions down to 3:
It’s nearly impossible to tell from this picture, but it’s five 24-cells inscribed in the 600-cell, with each vertex of the 600-cell being the vertex of just one of these five 24-cells. The trick for constructing it is to notice that the vertices of the 600-cell form a group sitting in the sphere of unit quaternions, and to find a 24-cell whose vertices form a subgroup.
The left cosets of a subgroup are the sets
They look like copies of ‘translated’, or in our case ‘rotated’, inside
Every point of
lies in exactly one coset.
In our example there are five cosets. Each is the set of vertices of a 24-cell inscribed in the 600-cell. Every vertex of the 600-cell lies in exactly one of these cosets. This gives our ‘compound of five 24-cells’.
It turns out this trick is part of a family of three tricks, each of which gives a nice compound of 4d regular polytopes. While I’ve been avoiding coordinates, I think they’ll help get the idea across now. Here’s a nice description of the 120 vertices of the 600-cell. We take these points:
and all those obtained by even permutations of the coordinates. So, we get
points of the first kind,
points of the second kind, and
points of the third kind, for a total of
points.
The 16 points of the first kind are the vertices of a 4-dimensional hypercube, the 4d analogue of a cube:
The 8 points of the second kind are the vertices of a 4-dimensional orthoplex, the 4d analogue of an octahedron:
The hypercube and orthoplex are dual to each other. Taking both their vertices together we get the 16 + 8 = 24 vertices of the 24-cell, which is self-dual:
The hypercube, orthoplex and 24-cell are regular polytopes, as is the 600-cell.
Now let’s think of any point in 4-dimensional space as a quaternion:
If we do this, we can check that the 120 vertices of the 600-cell form a group under quaternion multiplication. As mentioned in Part 1, this group is called the binary icosahedral group or because it’s a double cover of the rotational symmetry group of an icosahedron (or dodecahedron).
We can also check that the 24 vertices of the 24-cell form a group under quaternion multiplication. As mentioned in Part 1, this is called the binary tetrahedral group or because it’s a double cover of the rotational symmetry group of a tetrahedron.
All this is old news. But it’s even easier to check that the 8 vertices of the orthoplex form a group under quaternion multiplication: they’re just
This group is often called the quaternion group or It too is a double cover of a group of rotations! The 180° rotations about the
and
axes square to 1 and commute with each other; up in the double cover of the rotation group (the unit quaternions, or
) they give elements that square to -1 and anticommute with each other.
Furthermore, the 180° rotations about the and
axes are symmetries of a regular tetrahedron! This is easiest to visualize if you inscribe the tetrahedron in a cube thus:
So, up in the double cover of the 3d rotation group we get a chain of subgroups
which explains why we’re seeing an orthoplex inscribed in a 24-cell inscribed in a 600-cell! This explanation is more satisfying to me than the one involving coordinates.
Alas, I don’t see how to understand the hypercube inscribed in the 24-cell in quite this way, since the hypercube is not a subgroup of the unit quaternions. It certainly wasn’t in the coordinates I gave before—but worse, there’s no way to rotate the hypercube so that it becomes a subgroup. There must be something interesting to say here, but I don’t know it. So, I’ll forget the hypercube for now.
Instead, I’ll use group theory to do something nice with the orthoplex.
First, look at the orthoplexes sitting inside the 24-cell! We’ve got 8-element subgroup of a 24-element group:
so it has three right cosets, each forming the vertices of an orthoplex inscribed in the 24-cell. So, we get compound of three orthoplexes: a way of partitioning the vertices of the 24-cell into those of three orthoplexes.
Second, look at the orthoplexes sitting inside the 600-cell! We’ve got 8-element subgroup of a 120-element group:
so it has 15 right cosets, each forming the vertices of an orthoplex inscribed in the 600-cell. So, we get a compound of 15 orthoplexes: a way of partitioning the vertices of the 600-cell into those of 15 orthoplexes.
And third, these fit nicely with what we saw last time: the 24-cells sitting inside the 600-cell! We saw a 24-element subgroup of a 120-element group
so it has 5 right cosets, each forming the vertices of a 24-cell inscribed in the 600-cell. That gave us the compound of five 24-cells: a way of partitioning the vertices of the 600-cell into those of five 24-cells.
There are some nontrivial counting problems associated with each of these three compounds. David Roberson has already solved most of these.
1) How many ways are there of inscribing an orthoplex in a 24-cell?
2) How many ways are there of inscribing a compound of three orthoplexes in a 24-cell?
3) How many ways are there of inscribing an orthoplex in a 600-cell? David used a computer to show there are 75. Is there a nice human-understandable argument?
4) How many ways are there of inscribing a compound of 15 orthoplexes in a 600-cell? David used a computer to show there are 280. Is there a nice human-understandable argument?
5) How many ways are there of inscribing a 24-cell in a 600-cell? David used a computer to show there are 25. Is there a nice human-understandable argument?
4) How many ways are there of inscribing a compound of five 24-cells in a 600-cell? David used a computer to show there are 10. Is there a nice human-understandable argument? (It’s pretty easy to prove that 10 is a lower bound.)
For those who prefer visual delights to math puzzles, here is a model of the compound of 15 orthoplexes, cleverly projected from 4 dimensions down to 3, made by David Richter and some friends:
It took four people 6 hours to make this! Click on the image to learn more about this amazing shape, and explore David Richter’s pages to see more compounds.
So far my tale has not encompassed the 120-cell, which is the dual of the 600-cell. This has 600 vertices and 120 dodecahedral faces:
Unfortunately, like the hypercube, the vertices of the 120-cell cannot be made into a subgroup of the unit quaternions. I’ll need some other idea to think about them in a way that I enjoy. But the 120-cell is amazing because every regular polytope in 4 dimensions can be inscribed in the 120-cell.
For example, we can inscribe the orthoplex in the 120-cell. Since the orthoplex has 8 vertices while the 120-cell has 600, and
we might hope for a compound of 75 orthoplexes whose vertices, taken together, are those of the 120-cell. And indeed it exists… and David Richter and his friends have built a model!
Image credits
You can click on any image to see its source. The photographs of models of the compound of five 24-cells and the compound of 15 orthoplexes are due to David Richter and friends. The shiny ball-and-strut pictures of the tetrahedron in the cube and the 120-cells were made by Tom Ruen using Robert Webb’s Stella software and placed on Wikicommons. The 2d projections of the hypercube, orthoplex and 24-cell were made by Tom Ruen and placed into the public domain on Wikicommons.







I tried to think of some human readable proofs. Hopefully they are not too hand-wavy.
1) and 2) Let us consider the 24-cell given by the 16 points of the first kind and 8 points of the second kind that you described. Call the the set of 8 points of the second kind . Now partition the 16 points of the first kind into two sets: the points with an odd number of minus signs (call this set
. Now partition the 16 points of the first kind into two sets: the points with an odd number of minus signs (call this set  ), and the ones with an even number of minus signs (call this set
), and the ones with an even number of minus signs (call this set 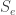 ). Now we have partitioned the points of the 24-cell into three sets of size 8. It is straightforward to check that the inner products within these sets are all
). Now we have partitioned the points of the 24-cell into three sets of size 8. It is straightforward to check that the inner products within these sets are all  or
or  , and that the inner products between two points in different sets is
, and that the inner products between two points in different sets is  . This shows that a 24-cell contains exactly 3 orthoplexes and thus has only one partition into three orthoplexes. Actually, this also shows that a 24-cell is exactly a set three mutually unbiased bases in
. This shows that a 24-cell contains exactly 3 orthoplexes and thus has only one partition into three orthoplexes. Actually, this also shows that a 24-cell is exactly a set three mutually unbiased bases in  (plus the antipodes).
(plus the antipodes).
3) This one is not too bad, you can basically just count them. First, note that an orthoplex is just an orthonormal basis plus the antipodes of all the vectors in the basis. To make things a bit simpler, we will consider a vector/point of the 600-cell and its antipode the same. So the 120 vertices of the 600-cell become 60 lines through the origin, and an orthoplex is a set of four mutually orthogonal lines. We will just pick the lines for our orthoplex one at a time. First, we have 60 choices for the first one, and they are all equivalent since the symmetry group of the 600-cell can map any one to any other one. So now we must pick the second element of our orthoplex. To determine how many choices we have here, we can assume without loss of generality that our first choice was the point (and its antipode). There are then 3 choices for the second point/line coming from the second kind of points (6 but divided by 2 because antipodes are the same), and there are
(and its antipode). There are then 3 choices for the second point/line coming from the second kind of points (6 but divided by 2 because antipodes are the same), and there are 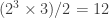 choices of points/lines of the third kind (all the ones with 0 in the first coordinate). So in total we have
choices of points/lines of the third kind (all the ones with 0 in the first coordinate). So in total we have  choices for the second element of our orthoplex. Now, note that again the symmetry of the 600-cell says that all choices for these first two elements are the same, since any two orthogonal vectors from the 600-cell can be mapped to any other two (in any order). So we may assume that the first two chosen are
choices for the second element of our orthoplex. Now, note that again the symmetry of the 600-cell says that all choices for these first two elements are the same, since any two orthogonal vectors from the 600-cell can be mapped to any other two (in any order). So we may assume that the first two chosen are  and
and 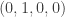 . It is easy to see that there are only 2 choices for the third element of our orthoplex, and then the final choice is determined for us. Thus we had
. It is easy to see that there are only 2 choices for the third element of our orthoplex, and then the final choice is determined for us. Thus we had 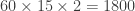 choices for our orthoplex. But we could have picked the same four elements in any order! So we actually have
choices for our orthoplex. But we could have picked the same four elements in any order! So we actually have  orthoplexes contained in the 600-cell. You mentioned that you can obtain a partition of the 600-cell into 15 orthoplexes by considering the cosets of the subgroup
orthoplexes contained in the 600-cell. You mentioned that you can obtain a partition of the 600-cell into 15 orthoplexes by considering the cosets of the subgroup  . Is it possible to find five distinct isomorphic copies of
. Is it possible to find five distinct isomorphic copies of  whose cosets would then give all of the 75 orthoplexes? This might be of help with puzzle (4).
whose cosets would then give all of the 75 orthoplexes? This might be of help with puzzle (4).
4) I don’t have a human proof here. I’m still thinking about it, but I think it might be difficult. The only idea I really have is to consider the graph that I mentioned last time: the vertices are the points of the 600-cell, two points are adjacent if their inner product is not
that I mentioned last time: the vertices are the points of the 600-cell, two points are adjacent if their inner product is not  or
or  . Then the maximum independent sets in
. Then the maximum independent sets in  are exactly the orthoplexes of the 600-cell, and the 15-colorings of
are exactly the orthoplexes of the 600-cell, and the 15-colorings of  are exactly the partitions of the 600-cell into 15 orthoplexes. We can maybe make things easier for ourselves by merging every point with its antipode. This doesn’t really change anything because every point always receives the same color as its antipode in a 15-coloring of
are exactly the partitions of the 600-cell into 15 orthoplexes. We can maybe make things easier for ourselves by merging every point with its antipode. This doesn’t really change anything because every point always receives the same color as its antipode in a 15-coloring of  (since such a coloring is a partition into orthoplexes). All this does is give us a smaller graph, call it
(since such a coloring is a partition into orthoplexes). All this does is give us a smaller graph, call it  , to work with, and the 15-colorings of
, to work with, and the 15-colorings of  are in one-to-one correspondence to the 15-colorings of
are in one-to-one correspondence to the 15-colorings of  . In any case, the value of the Lovasz theta number of the complement of
. In any case, the value of the Lovasz theta number of the complement of  (or
(or 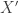 ) is equal to 15, the chromatic number of these graphs. The Lovasz theta number of the complement of a graph is always a lower bound on the chromatic number, but in this case they are equal, and this means that a 15-coloring of
) is equal to 15, the chromatic number of these graphs. The Lovasz theta number of the complement of a graph is always a lower bound on the chromatic number, but in this case they are equal, and this means that a 15-coloring of  or
or 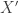 gives an optimal solution for the Lovasz theta number of their complements. I won’t go into much detail here, because it would go on forever, but the set of optimal solutions for (a certain formulation of) the Lovasz theta number forms a convex set, and I would be willing to bet that the 15-colorings of
gives an optimal solution for the Lovasz theta number of their complements. I won’t go into much detail here, because it would go on forever, but the set of optimal solutions for (a certain formulation of) the Lovasz theta number forms a convex set, and I would be willing to bet that the 15-colorings of  or
or 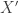 are extreme points of this set (but I do not have a proof of this). So investigation of this convex set may be of some help, but again, this seems difficult. Chris Godsil, Brendan Rooney, Robert Samal, Antonios Varvitsiotis, and myself have done some work on describing the set of all optimal solutions for Lovasz theta in some cases: https://arxiv.org/abs/1512.04972 and https://arxiv.org/abs/1610.10002. But honestly I think there is probably a better approach using group theory.
are extreme points of this set (but I do not have a proof of this). So investigation of this convex set may be of some help, but again, this seems difficult. Chris Godsil, Brendan Rooney, Robert Samal, Antonios Varvitsiotis, and myself have done some work on describing the set of all optimal solutions for Lovasz theta in some cases: https://arxiv.org/abs/1512.04972 and https://arxiv.org/abs/1610.10002. But honestly I think there is probably a better approach using group theory.
5) We can use our previous solutions to help us here. An understanding of the proof of (3) lets us know that the symmetry group of the 600-cell acts transitively on the set of orthoplexes inscribed in the 600-cell (it acts transitively on pairs of orthogonal points, and once two orthogonal points are fixed the remaining elements of the orthoplex are determined). So all the orthoplexes are “the same”. Let us consider the one given by the eight points of the second kind. Since there are some 24-cells in the 600-cell, it must be possible to complete this orthoplex to a 24-cell. How many ways are there to do this? The proof of (1) and (2) tells us that each of the additional 16 points we add must have inner product with all of the 8 points we started with. Clearly, the only possible choices are the 16 points of the first kind, and we must take all of them. So every orthoplex that is inscribed in the 600-cell can be completed in a unique way to an inscribed 24-cell. So we get a 24-cell for each orthoplex, which gives us 75. But wait! We over-counted again. Of course, some orthoplexes will be completed to the same 24-cell. Here we use our solution to (1) and (2) again. Every 24-cell is the disjoint union of three orthoplexes, so these three orthoplexes will all be completed to the same 24-cell. Thus we must divide by 3, and we get that there are
with all of the 8 points we started with. Clearly, the only possible choices are the 16 points of the first kind, and we must take all of them. So every orthoplex that is inscribed in the 600-cell can be completed in a unique way to an inscribed 24-cell. So we get a 24-cell for each orthoplex, which gives us 75. But wait! We over-counted again. Of course, some orthoplexes will be completed to the same 24-cell. Here we use our solution to (1) and (2) again. Every 24-cell is the disjoint union of three orthoplexes, so these three orthoplexes will all be completed to the same 24-cell. Thus we must divide by 3, and we get that there are  24-cells inscribed in the 600-cell. These must also be exactly the 25 that you get by considering the right cosets of the 5 different copies of the binary tetrahedral group that you described. This also means that the left cosets give the same 25 (maybe this is obvious but I am not as familiar as you with the group theory here). Actually, question for you: how do we know that the left cosets give different partitions of the 600-cell into 24-cells from the partitions given by the right cosets? I guess this is equivalent to the subgroup not being normal.
24-cells inscribed in the 600-cell. These must also be exactly the 25 that you get by considering the right cosets of the 5 different copies of the binary tetrahedral group that you described. This also means that the left cosets give the same 25 (maybe this is obvious but I am not as familiar as you with the group theory here). Actually, question for you: how do we know that the left cosets give different partitions of the 600-cell into 24-cells from the partitions given by the right cosets? I guess this is equivalent to the subgroup not being normal.
6) I think you have a typo in the post, because the last puzzle is actually labeled (4). Again, I do not have a human proof here, but it seems more tractable than (4). Since the symmetry group acts transitively on the set of orthoplexes inscribed in the 600-cell, the argument from (5) shows that the same is true of the 24-cells, which may be useful. We know how to construct 10 partitions of the 600-cell into 24-cells by taking the left and right cosets of the five copies of the binary tetrahedral group sitting inside the binary icosahedral group
sitting inside the binary icosahedral group  , but we want to show that these are all the ways to do this. We also know from (5) that the only 24-cells are the cosets of the five copies of
, but we want to show that these are all the ways to do this. We also know from (5) that the only 24-cells are the cosets of the five copies of  contained in
contained in  . I checked in Sage, and it turns out that given any two disjoint 24-cells inscribed in the 600-cell, there are exactly three 24-cells disjoint from both of these, and together these five 24-cells partition the 600-cell (so the three additional ones are also mutually disjoint). Given that we know that the only 10 partitions into 24-cells come from the coset construction, this implies that given any two disjoint 24-cells, they are either both left or both right cosets of the same copy of
. I checked in Sage, and it turns out that given any two disjoint 24-cells inscribed in the 600-cell, there are exactly three 24-cells disjoint from both of these, and together these five 24-cells partition the 600-cell (so the three additional ones are also mutually disjoint). Given that we know that the only 10 partitions into 24-cells come from the coset construction, this implies that given any two disjoint 24-cells, they are either both left or both right cosets of the same copy of  . Maybe proving this by hand would not be too hard? Suppose we can prove this, and consider a partition of the 600-cell into five 24-cells. By what we have assumed, any two of these five 24-cells must both be left or both be right cosets of some fixed copy of
. Maybe proving this by hand would not be too hard? Suppose we can prove this, and consider a partition of the 600-cell into five 24-cells. By what we have assumed, any two of these five 24-cells must both be left or both be right cosets of some fixed copy of  . But then we are done, since we can fix one 24-cell and then apply this statement to it and the other four 24-cells in turn. So we just need to show that given two disjoint cosets
. But then we are done, since we can fix one 24-cell and then apply this statement to it and the other four 24-cells in turn. So we just need to show that given two disjoint cosets 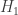 and
and 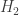 of two, possibly different, copies of
of two, possibly different, copies of  , there must be some copy of
, there must be some copy of  for which
for which 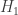 and $latex
and $latex 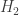 are either both left or both right cosets. By symmetry, we may even assume that
are either both left or both right cosets. By symmetry, we may even assume that 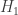 is one of the copies of
is one of the copies of  (and thus
(and thus 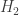 is a proper coset of a different copy of
is a proper coset of a different copy of  in the nontrivial case).
in the nontrivial case).
4) is wrong. There are only 10 ways to vertex-inscribe the uniform compound of 15 16-cells into a 600-cell, because the former shares its symmetry group (which is abstractly , by the way) with the compound of 5 24-cells.
, by the way) with the compound of 5 24-cells.