This is an expanded version of my G+ post, which was a watered-down version of Greg Egan’s G+ post and the comments on that. I’ll start out slow, and pick up speed as I go.
Quantum mechanics meets the dodecahedron
In quantum mechanics, the position of a particle is not a definite thing: it’s described by a ‘wavefunction’. This says how probable it is to find the particle at any location… but it also contains other information, like how probable it is to find the particle moving at any velocity.
Take a hydrogen atom, and look at the wavefunction of the electron.
Question 1. Can we make the electron’s wavefunction have all the rotational symmetries of a dodecahedron—that wonderful Platonic solid with 12 pentagonal faces?
Yes! In fact it’s too easy: you can make the wavefunction look like whatever you want.
So let’s make the question harder. Like everything else in quantum mechanics, angular momentum can be uncertain. In fact you can never make all 3 components of angular momentum take definite values simultaneously! However, there are lots of wavefunctions where the magnitude of an electron’s angular momentum is completely definite.
This leads naturally to the next question, which was first posed by Gerard Westendorp:
Question 2. Can an electron’s wavefunction have a definite magnitude for its angular momentum while having all the rotational symmetries of a dodecahedron?
Yes! And there are infinitely many ways for this to happen! This is true even if we neglect the radial dependence of the wavefunction—that is, how it depends on the distance from the proton. Henceforth I’ll always do that, which lets us treat the wavefunction as a function on a sphere. And by the way, I’m also ignoring the electron’s spin! So, whenever I say ‘angular momentum’ I mean orbital angular momentum: the part that depends only on the electron’s position and velocity.
Question 2 has a trivial solution that’s too silly to bother with. It’s the spherically symmetric wavefunction! That’s invariant under all rotations. The real challenge is to figure out the simplest nontrivial solution. Egan figured it out, and here’s what it looks like:
The rotation here is just an artistic touch. Really the solution should be just sitting there, or perhaps changing colors while staying the same shape.
In what sense is this the simplest nontrivial solution? Well, the magnitude of the angular momentum is equal to
where the number is quantized: it can only take values 0, 1, 2, 3,… and so on.
The trivial solution to Question 2 has The first nontrivial solution has
Why 6? That’s where things get interesting. We can get it using the 6 lines connecting opposite faces of the dodecahedron!
I’ll explain later how this works. For now, let’s move straight on to a harder question:
Question 3. What’s the smallest choice of where we can find two linearly independent wavefunctions that both have the same
and both have all the rotational symmetries of a dodecahedron?
It turns out to be And Egan created an image of a wavefunction oscillating between these two possibilities!
But we can go a lot further:
Question 4. For each how many linearly independent functions on the sphere have that value of
and all the rotational symmetries of a dodecahedron?
For ranging from 0 to 29 there are either none or one. There are none for these numbers:
1, 2, 3, 4, 5, 7, 8, 9, 11, 13, 14, 17, 19, 23, 29
and one for these numbers:
0, 6, 10, 12, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28
The pattern continues as follows. For ranging from 30 to 59 there are either one or two. There is one for these numbers:
31, 32, 33, 34, 35, 37, 38, 39, 41, 43, 44, 47, 49, 53, 59
and two for these numbers:
30, 36, 40, 42, 45, 46, 48, 50, 51, 52, 54, 55, 56, 57, 58
The numbers in these two lists are just 30 more than the numbers in the first two lists! And it continues on like this forever: there’s always one more linearly independent solution for than there is for
Question 5. What’s special about these numbers from 0 to 29?
0, 6, 10, 12, 15, 18, 20, 21, 22, 24, 25, 26, 27, 28
You don’t need to know tons of math to figure this out—but I guess it’s a sort of weird pattern-recognition puzzle unless you know which patterns are likely to be important here. So I’ll give away the answer.
Here’s the answer: these are the numbers below 30 that can be written as sums of the numbers 6, 10 and 15.
But the real question is why? Also: what’s so special about the number 30?
The short, cryptic answer is this. The dodecahedron has 6 axes connecting the centers of opposite faces, 10 axes connecting opposite vertices, and 15 axes connecting the centers of opposite edges. The least common multiple of these numbers is 30.
But this requires more explanation!
For this, we need more math. You may want to get off here. But first, let me show you the solutions for and
as drawn by Greg Egan. I’ve already showed you
which we could call the quantum dodecahedron:
Here is which looks like a quantum icosahedron:
And here is :
Maybe this deserves to be called a quantum Coxeter complex, since the Coxeter complex for the group of rotations and reflections of the dodecahedron looks like this:
Functions with icosahedral symmetry
The dodecahedron and icosahedron have the same symmetries, but for some reason people talk about the icosahedron when discussing symmetry groups, so let me do that.
So far we’ve been looking at the rotational symmetries of the icosahedron. These form a group called or
for short, with 60 elements. We’ve been looking for certain functions on the sphere that are invariant under the action of this group. To get them all, we’ll first get ahold of all polynomials on
that are invariant under the action of this group Then we’ll restrict these to the sphere.
To save time, we’ll use the work of Claude Chevalley. He looked at rotation and reflection symmetries of the icosahedron. These form the group also known as
but let’s call it
for short. It has 120 elements, but never confuse it with two other groups with 120 elements: the symmetric group on 5 letters, and the binary icosahedral group.
Chevalley found all polynomials on that are invariant under the action of this bigger group
These invariant polynomials form an algebra, and Chevalley showed that this algebra is freely generated by 3 homogeneous polynomials:
• of degree 2.
• of degree 6. To get this we take the dot product of
with each of the 6 vectors joining antipodal vertices of the icosahedron, and multiply them together.
• of degree 10. To get this we take the dot product of
with each of the 10 vectors joining antipodal face centers of the icosahedron, and multiply them together.
So, linear combinations of products of these give all polynomials on invariant under all rotation and reflection symmetries of the icosahedron.
But we want the polynomials that are invariant under just rotational symmetries of the icosahedron! To get all these, we need an extra generator:
• of degree 15. To get this we take the dot product of
with each of the 15 vectors joining antipodal edge centers of the icosahedron, and multiply them together.
You can check that this is invariant under rotational symmetries of the icosahedron. But unlike our other polynomials, this one is not invariant under reflection symmetries! Because 15 is an odd number, switches sign under ‘total inversion’—that is, replacing
with
This is a product of three reflection symmetries of the icosahedron.
Thanks to Egan’s extensive computations, I’m completely convinced that and
generate the algebra of all
-invariant polynomials on
I’ll take this as a fact, even though I don’t have a clean, human-readable proof. But someone must have proved it already—do you know where?
Since we now have 4 polynomials on they must obey a relation. Egan figured it out:
The exact coefficients depend on some normalization factors used in defining and
Luckily the details don’t matter much. All we’ll really need is that this relation expresses
in terms of the other generators. And this fact is easy to see without any difficult calculations!
How? Well, we’ve seen is unchanged by rotations, while it changes sign under total inversion. So, the most any rotation or reflection symmetry of the icosahedron can do to
is change its sign. This means that
is invariant under all these symmetries. So, by Chevalley’s result, it must be a polynomial in
and
.
So, we now have a nice description of the -invariant polynomials on
in terms of generators and relations. Each of these gives an
-invariant function on the sphere. And Leo Stein, a postdoc at Caltech who has a great blog on math and physics, has kindly created some images of these.
The polynomial is spherically symmetric so it’s too boring to draw. The polynomial
of degree 6, looks like this when restricted to the sphere:
Since it was made by multiplying linear functions, one for each axis connecting opposite vertices of an icosahedron, it shouldn’t be surprising that we see blue blobs centered at these vertices.
The polynomial of degree 10, looks like this:
Here the blue blobs are centered on the icosahedron’s 20 faces.
Finally, here’s of degree 15:
This time the blue blobs are centered on the icosahedron’s 30 edges.
Now let’s think a bit about functions on the sphere that arise from polynomials on Let’s call them algebraic functions on the sphere. They form an algebra, and it’s just the algebra of polynomials on
modulo the relation
since the sphere is the set
It makes no sense to talk about the ‘degree’ of an algebraic function on the sphere, since the relation equates polynomials of different degree. What makes sense is the number
that I was talking about earlier!
The group acts by rotation on the space of algebraic functions on the sphere, and we can break this space up into irreducible representations of
It’s a direct sum of irreps, one of each ‘spin’
So, we can’t talk about the degree of a function on the sphere, but we can talk about its value. On the other hand, it’s very convenient to work with homogeneous polynomials on
which have a definite degree—and these restrict to functions on the sphere. How can we relate the degree and the quantity
?
Here’s one way. The polynomials on form a graded algebra. That means it’s a direct sum of vector spaces consisting of homogeneous polynomials of fixed degree, and if we multiply two homogeneous polynomials their degrees add. But the algebra of polynomials restricted to the sphere is merely filtered algebra.
What does this mean? Let be the algebra of all algebraic functions on the sphere, and let
consist of those that are restrictions of polynomials of degree
Then:
1)
and
2)
and
3) if we multiply a function in by one in
we get one in
That’s what a filtered algebra amounts to.
But starting from a filtered algebra, we can get a graded algebra! It’s called the associated graded algebra.
To do this, we form
and let
Then has a product where multiplying a guy in
and one in
gives one in
So, it’s indeed a graded algebra! For the details, see Wikipedia, which manages to make it look harder than it is. The basic idea is that we multiply in
and then ‘ignore terms of lower degree’. That’s what
is all about.
Now I want to use two nice facts. First, is the spin-
representation of
Second, there’s a natural map from any filtered algebra to its associated graded algebra, which is an isomorphism of vector spaces (though not of algebras). So, we get an natural isomorphism of vector spaces
from the algebraic functions on the sphere to the direct sum of all the spin- representations!
Now to the point: because this isomorphism is natural, it commutes with symmetries, so we can also use it to study algebraic functions on the sphere that are invariant under a group of linear transformations of
Before tackling the group we’re really interested in, let’s try the group of rotation and reflection symmetries of the icosahedron, As I mentioned, Chevalley worked out the algebra of polynomials on
that are invariant under this bigger group. It’s a graded commutative algebra, and it’s free on three generators:
of degree 2,
of degree 6, and
of degree 10.
Starting from here, to get the algebra of -invariant algebraic functions on the sphere, we mod out by the relation
This gives a filtered algebra which I’ll call
(It’s common to use a superscript with the name of a group to indicate that we’re talking about the stuff that’s invariant under some action of that group.) From this we can form the associated graded algebra
where
If you’ve understood everything I’ve been trying to explain, you’ll see that is the space of all functions on the sphere that transform in the spin-
representation and are invariant under the rotation and reflection symmetries of the icosahedron.
But now for the fun part: what is this space like? By the work of Chevalley, the algebra is spanned by products
but since we have the relation and no other relations, it has a basis given by products
So, the space has a basis of products like this whose degree is
meaning
Thus, the space we’re really interested in:
has a basis consisting of equivalence classes
where
So, we get:
Theorem 1. The dimension of the space of functions on the sphere that lie in the spin- representation of
and are invariant under the rotation and reflection symmetries of the icosahedron equals the number of ways of writing
as an unordered sum of 6’s and 10’s.
Let’s see how this goes:
: dimension 1, with basis
: dimension 0
: dimension 0
: dimension 0
: dimension 0
: dimension 0
: dimension 1, with basis
: dimension 0
: dimension 0
: dimension 0
: dimension 1, with basis
: dimension 0
: dimension 1, with basis
: dimension 0
: dimension 0
: dimension 0
: dimension 1, with basis
: dimension 0
: dimension 1, with basis
: dimension 0
: dimension 1, with basis
: dimension 0
: dimension 1, with basis
: dimension 0
: dimension 1, with basis
: dimension 0
: dimension 1, with basis
: dimension 0
: dimension 1, with basis
: dimension 0
: dimension 2, with basis
So, the story starts out boring, with long gaps. The odd numbers are completely uninvolved. But it heats up near the end, and reaches a thrilling climax at At this point we get two linearly independent solutions, because 30 is the least common multiple of the degrees of
and
It’s easy to see that from here on the story ‘repeats’ with period 30, with the dimension growing by 1 each time:
Now, finally, we are to tackle Question 4 from the first part of this post: for each how many linearly independent functions on the sphere have that value of
and all the rotational symmetries of a dodecahedron?
We just need to repeat our analysis with the group of rotational symmetries of the dodecahedron, replacing the bigger group
We start with algebra of polynomials on that are invariant under
. As we’ve seen, this is a graded commutative algebra with four generators:
as before, but also
of degree 15. To make up for this extra generator there’s an extra relation, which expresses
in terms of the other generators.
Starting from here, to get the algebra of -invariant algebraic functions on the sphere, we mod out by the relation
This gives a filtered algebra I’ll call
Then we form the associated graded algebra
where
What we really want to know is the dimension of since this is the space of functions on the sphere that transform in the spin-
representation and are invariant under the rotational symmetries of the icosahedron.
So, what’s this space like? The algebra is spanned by products
but since we have the relation and a relation expressing
in terms of other generators, it has a basis given by products
where
So, the space has a basis of products like this whose degree is
meaning
and
Thus, the space we’re really interested in:
has a basis consisting of equivalence classes
where
and
So, we get:
Theorem 2. The dimension of the space of functions on the sphere that lie in the spin- representation of
and are invariant under the rotational symmetries of the icosahedron equals the number of ways of writing
as an unordered sum of 6’s, 10’s and at most one 15.
Let’s work out these dimensions explicitly, and see how the extra generator changes the story! Since it has degree 15, it contributes some solutions for odd values of
But when we reach the magic number 30, this extra generator loses its power:
has degree 30, but it’s a linear combination of other things.
: dimension 1, with basis
: dimension 0
: dimension 0
: dimension 0
: dimension 0
: dimension 0
: dimension 1, with basis
: dimension 0
: dimension 0
: dimension 0
: dimension 1, with basis
: dimension 0
: dimension 1, with basis
: dimension 0
: dimension 0
: dimension 1, with basis
: dimension 1, with basis
: dimension 0
: dimension 1, with basis
: dimension 0
: dimension 1, with basis
: dimension 1, with basis
: dimension 1, with basis
: dimension 0
: dimension 1, with basis
: dimension 1, with basis
: dimension 1, with basis
: dimension 1, with basis
: dimension 1, with basis
: dimension 0
: dimension 2, with basis
From here on the story ‘repeats’ with period 30, with the dimension growing by 1 each time:
So, we’ve more or less proved everything that I claimed in the first part. So we’re done!
Postscript
But I can’t resist saying a bit more.
First, there’s a very different and somewhat easier way to compute the dimensions in Theorems 1 and 2. It uses the theory of characters, and Egan explained it in a comment on the blog post on which this is based.
Second, if you look in these comments, you’ll also see a lot of material about harmonic polynomials on —that is, those obeying the Laplace equation. These polynomials are very nice when you’re trying to decompose the space of functions on the sphere into irreps of
The reason is that the harmonic homogeneous polynomials of degree
when restricted to the sphere, give you exactly the spin-
representation!
If you take all homogeneous polynomials of degree and restrict them to the sphere you get a lot of ‘redundant junk’. You get the spin-
rep, plus the spin-
rep, plus the spin-
rep, and so on. The reason is the polynomial
and its powers: if you have a polynomial living in the spin- rep and you multiply it by
you get another one living in the spin-
rep, but you’ve boosted the degree by 2.
Layra Idarani pointed out that this is part of a nice general theory. But I found all this stuff slightly distracting when I was trying to prove Theorems 1 and 2 assuming that we had explicit presentations of the algebras of – and
-invariant polynomials on
So, instead of introducing facts about harmonic polynomials, I decided to use the ‘associated graded algebra’ trick. This is a more algebraic way to ‘eliminate the redundant junk’ in the algebra of polynomials and chop the space of functions on the sphere into irreps of
Also, Egan and Idarani went ahead and considered what happens when we replace the icosahedron by another Platonic solid. It’s enough to consider the cube and tetrahedron. These cases are actually subtler than the icosahedron! For example, when we take the dot product of with each of the 10 vectors joining antipodal face centers of the cube, and multiply them together, we get a polynomial that’s not invariant under rotations of the cube! Up to a constant it’s just
and this changes sign under some rotations.
People call this sort of quantity, which gets multiplied by a number under transformations instead of staying the same, a semi-invariant. The reason we run into semi-invariants for the cube and tetrahedron is that their rotational symmetry groups, and
have nontrivial abelianizations, namely
and
The abelianization of
is trivial.
Egan summarized the story as follows:
Just to sum things up for the cube and the tetrahedron, since the good stuff has ended up scattered over many comments:
For the cube, we define:
A of degree 4 from the cube’s vertex-axes, a full invariant
B of degree 6 from the cube’s edge-centre-axes, a semi-invariant
C of degree 3 from the cube’s face-centre-axes, a semi-invariantWe have full invariants:
A of degree 4
C2 of degree 6
BC of degree 9B2 can be expressed in terms of A, C and P, so we never use it, and we use BC at most once.
So the number of copies of the trivial rep of the rotational symmetry group of the cube in spin ℓ is the number of ways to write ℓ as an unordered sum of 4, 6 and at most one 9.
For the tetrahedron, we embed its vertices as four vertices of the cube. We then define:
V of degree 4 from the tet’s vertices, a full invariant
E of degree 3 from the tet’s edge-centre axes, a full invariantAnd the B we defined for the embedding cube serves as a full invariant of the tet, of degree 6.
B2 can be expressed in terms of V, E and P, so we use B at most once.
So the number of copies of the trivial rep of the rotational symmetry group of the tetrahedron in spin ℓ is the number of ways to write ℓ as a sum of 3, 4 and at most one 6.
All of this stuff reminds me of a baby version of the theory of modular forms. For example, the algebra of modular forms is graded by ‘weight’, and it’s the free commutative algebra on a guy of weight 4 and a guy of weight 6. So, the dimension of the space of modular forms of weight is the number of ways of writing
as an unordered sum of 4’s and 6’s. Since the least common multiple of 4 and 6 is 12, we get a pattern that ‘repeats’, in a certain sense, mod 12. Here I’m talking about the simplest sort of modular forms, based on the group
But there are lots of variants, and I have the feeling that this post is secretly about some sort of variant based on finite subgroups of
instead of infinite discrete subgroups.
There’s a lot more to say about all this, but I have to stop or I’ll never stop. Please ask questions and if you want me to say more!










Looks like you copy/pasted the URL of the gif for the R polynomial in place of the S polynomial, which is here: http://math.ucr.edu/home/baez/mathematical/stein_invariants/stein_icosahedral_invariant_S.gif
Thanks! Fixed!
Typos: four instances of “latex” missing before \mathrm and \mathbb.
How does Wikipedia do that so darn well?
Thanks! I thought this stuff was much too nice to make people scour our long conversation for the facts and force them to mentally assemble these facts into a clear picture themselves.
Thanks for catching those flaws. Fixed!
Get a volunteer army of grad students from across the world to explain math they’ve just learned but don’t understand very well?
:star: <3 nice! came here after google recommended it in my newsfeed and thx to google for actually recommending a wordpress blog instead of something merely from the MSM!
general content reminds me of this brilliant paper by gilet on 2d circular wavefns, and believe it can be readily expanded to 3d to get similar results as those youre analyzing. ps it would be nice if your blog allowed wordpress “likes” :)
http://dotwave.org/quantumlike-statistics-of-deterministic-waveparticle-interactions-in-a-circular-cavity/
more on related areas
There happens to be a nice, albeit toy-ish, physical interpretation:
The buckminsterfullerene (C60) molecule has the same symmetry group as the icosahedron. The many-nuclei wavefunction of a rotational eigenstate of the molecule needs to have the same symmetries, because the 12C nuclei are bosons. This then becomes exactly the same problem as the one considered here. The result is that only the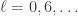 eigenvalues are permitted,
eigenvalues are permitted, 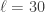 is permitted and doubly degenerate, etc.
is permitted and doubly degenerate, etc.
One can also think of what happens if you put fermions on the same molecule. (From my limited knowledge of physics, anyons don’t exist in 3 dimensions, do they?)
Is there published work on buckminsterfullerene that works out the permitted values of ? I’d really like to see that… it would be great to have a real-world application of this math.
? I’d really like to see that… it would be great to have a real-world application of this math.
The theory with fermions should also be very interesting. In my post I used a graded algebra that’s the direct sum of all the spin- representations for
representations for
but there’s also a bigger one that’s the direct sum of all the spin- representations for
representations for
The binary icosahedral group acts on this and one can look at the invariant elements, which form a subalgebra. This should be closely connected to the work of Klein, who figured out generators and relations for the
acts on this and one can look at the invariant elements, which form a subalgebra. This should be closely connected to the work of Klein, who figured out generators and relations for the  -invariant polynomials on the spin-
-invariant polynomials on the spin- representation
representation 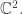 I describe those generators and relations here:
I describe those generators and relations here:
• From the icosahedron to E8.
Okay, now I’m psyched up to work this out! Greg and Bruce Bartlett and I have already done a lot of the necessary calculations.
And yes, there are no anyons in 3 or more dimensions.
I am glad to see your interest rekindled. The application side of this work seems most interesting and wide.
My interested never waned; I was just busy with other things.
I’m not very interested in the applications of these ideas; to me this is just fun pure math. My ‘real’ work is much more applied.
I don’t know of published work on the problem, unfortunately. This was just an amusing problem from an amusing professor. I’ll remember to ask him if he knows of any, though, and whether he has given some thought to the fermionic case (or, indeed, other interesting extensions of the problem).
Thanks for the link! Do you plan on posting the calculations you perform here (or on Google+, perhaps)? I would have loved to get involved, but there are some chores to attend to…
If and when I do anything interesting, you’ll hear about it here and/or on G+. I’ll read a bit about buckminsterfullerene.
Here’s a chart of buckyball energy levels from Wikipedia:
I don’t know how this is calculated or how the icosahedral symmetry is used. The rotational symmetry group has irreducible unitary representations of dimensions 1, 3, 3, 4 and 5. I believe all these representations are complexifications of real reps.
has irreducible unitary representations of dimensions 1, 3, 3, 4 and 5. I believe all these representations are complexifications of real reps.
They write:
I don’t know if ‘theoretical group activity’ means ‘activity by groups of theorists’ or ‘activity by group theorists’.
I believe the Wikipedia picture describes how the spectrum of a Hamiltonian that is rotationally invariant, and hence has a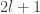 degeneracy for each
degeneracy for each  (not caring about the two spins they’ve shown), is split by a perturbation that has the
(not caring about the two spins they’ve shown), is split by a perturbation that has the  symmetry. The symbols on the right are just physics/chemistry-speak for the irreps of
symmetry. The symbols on the right are just physics/chemistry-speak for the irreps of  .
.
“Crystal field splitting” calculations of this sort are covered in many treatments of group theory in physics (e.g. Landau’s Course, Volume 3, Section 96).
The electrons of the molecule sit in the potential produced by its nuclei, which you could presumably write as a sum of a rotationally invariant function and one with icosahedral symmetry.
The Wikipedia page is alluding to something more complicated than what we’ve discussed: namely, the vibrational structure.
Actually, let me back up. The electronic structure is already more complicated than what we were discussing, because (1) it’s fermionic, not bosonic; and (2) it’s actually a many-electron wavefunction, not the simplistic single-electron wavefunction we usually think of.
But then there’s the comment you quoted, about vibrational bands. Besides the electronic structure, we could also worry about vibrations of the whole molecule. For small enough vibrations, we could use linear theory and decompose the displacements into radial and tangential deformations. The radial components can be decomposed into ordinary spherical harmonics, but the tangential components must be decomposed into vector spherical harmonics, of “electric” and “magnetic” type.
There’s clearly more fun in store, but it’s not for the faint of heart!
The structure of the vibrational spectrum (or a zero-th approximation to it) is actually not that difficult! It’s just a matter of writing down the representation of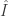 under which the normal mode coordinates transform, and decomposing it into the irreps.
under which the normal mode coordinates transform, and decomposing it into the irreps.
SO(3) isn’t involved in this; I’m pretty sure that John’s Wikipedia image describes crystal field splitting. The electron’s fermionic statistics doesn’t mean that the wavefunction has to be symmetric under icosahedral transformations. If electron-electron interactions didn’t play a part (not a very good assumption, but the whole discussion is on toy models), then the spectrum should in fact look like the picture’s right hand side. And after you fill this with independent electrons, you can just antisymmetrize their many-body wavefunction as the usual Slater determinant.
Hope this wasn’t too incoherent!
That made sense. But there should be a nice paper on this, somewhere, which fills in all the details. I’m not sure I want to dive into buckminsterfullerology. But some very good group theorists have done so, so there’s a lot to learn:
• Fan R. K. Chung , Bertram Kostant and Shlomo Sternberg, Groups and the buckyball.
Kostant and Sternberg were respected (almost feared) teachers of mine back when I was a grad student. This article starts with things I understand well…. but then it bumps into the outer automorphism of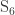 and shoots off into hyperspace.
and shoots off into hyperspace.
Infrared active eigenmodes (i.e. symmetry adapted coordinates, that also describe (resonant) vibrational motions) are those which change the dipole moment of the molecule. The transform all like the threefold degenerate ungerade representation called Tu in Mulliken notation.
In your lists of icosahedrally invariant polynomials you missed the l = 16 case of QR.
Thanks! Fixed!
This is a great write-up of the results! I wouldn’t have had the energy to do this. And it was interesting to see how you handled the restriction of the polynomials to the sphere.
John wrote:
I am not sure whether I understand this. That is how is here a degree polynomial as a representative of a base function in
polynomial as a representative of a base function in ![[Q^q R^r S^s]](https://s0.wp.com/latex.php?latex=%5BQ%5Eq+R%5Er+S%5Es%5D+&bg=ffffff&fg=333333&s=0&c=20201002) to be understood as a representation of a rotation?
to be understood as a representation of a rotation?
Not “a representation of a rotation”, but “a representation of the group of rotations, SO(3)”. A representation of a group G is a vector space V equipped with a linear transformation T(g): V → V for each g in G, such that
T(gh) = T(g) T(h)
and
T(1) = 1
The space of degree-ℓ polynomials in 3 variables is a representation of SO(3) in an obvious way. From this we can extract, in the manner I explained, the spin-ℓ representation of SO(3). The spin-ℓ representation has dimension (2ℓ+1), while the space of degree-ℓ polynomials in three variables is considerably larger.
John wrote:
Yes and represents a group element (here a rotation).
represents a group element (here a rotation). expressed in terms of the basis consisting of equivalence classes
expressed in terms of the basis consisting of equivalence classes
![[Q^q R^r S^s]](https://s0.wp.com/latex.php?latex=%5BQ%5Eq+R%5Er+S%5Es%5D+&bg=ffffff&fg=333333&s=0&c=20201002) . Do you use conjugation in a Clifford algebras for that?
. Do you use conjugation in a Clifford algebras for that?
So I would like to know how exactly is a
Sorry where exactly did you explain this in the post, I may have overlooked something but I can’t find this in the post.
Nad wrote:
No, I was trying to avoid all explicit formulas, so I used a standard principle in math: if you have a group acting on some set, and you build new set from that old set in a functorial way, the group also acts on this new set.
Rotations act on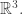 So, rotations act on anything functorially built from
So, rotations act on anything functorially built from 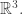 For example, they act on the algebra of all polynomials on
For example, they act on the algebra of all polynomials on 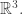 They also act on this algebra modulo the ideal generated by
They also act on this algebra modulo the ideal generated by  because this polynomial is invariant under rotations. I used
because this polynomial is invariant under rotations. I used  to stand for this algebra of polynomials mod
to stand for this algebra of polynomials mod 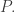
 is isomorphic to an algebra of functions on the sphere. Rotations also act on
is isomorphic to an algebra of functions on the sphere. Rotations also act on 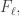 which is the subspace of
which is the subspace of  coming from polynomials of degree
coming from polynomials of degree  So, they also act on
So, they also act on 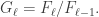 That’s the logic.
That’s the logic.
It’s right around here:
I defined the vector space Gℓ in a rather abstract way, which I reviewed just now. But since it was built from things that the rotation group acts on, it’s obviously some representation of SO(3). It’s more work to show that it’s the spin-ℓ representation. But that’s ‘well-known’, so I didn’t show it: I just stated it.
If you want to check it, show that its dimension is 2ℓ+1 and that it has a cyclic vector. That implies it’s an irreducible representation of SO(3) with dimension 2ℓ+1. And that implies it’s isomorphic to the spin-ℓ representation.
This may be frustratingly abstract. Greg Egan took a more concrete approach and probably has everything programmed into Mathematica. I believe he likes to think of the spin-ℓ representation as the space of degree-ℓ polynomials on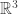 that obey Laplace’s equation. These are called [regular solid harmonics-(https://en.wikipedia.org/wiki/Solid_harmonics), and they restrict, on the sphere, to spherical harmonics. That’s a fine approach, but I felt it was a bit distracting to bring Laplace’s equation into the game.
that obey Laplace’s equation. These are called [regular solid harmonics-(https://en.wikipedia.org/wiki/Solid_harmonics), and they restrict, on the sphere, to spherical harmonics. That’s a fine approach, but I felt it was a bit distracting to bring Laplace’s equation into the game.
John wrote:
I just saw that meanwhile some couple of hours ago he has written something:
https://plus.google.com/113086553300459368002/posts/bhp6yYZEX4u
there he -similarily like me seems to ask himself- how the rotations relate to the polynomials. In the post he uses a special sub algebra of a special Clifford algebra, namely the quaternions to construct a polynomial (which he then can interpret then though as a higher dimensional analog of a spherical harmonic. hm?)
I am way to tired now to read and understand whats written here:
https://en.wikipedia.org/wiki/Clifford_algebra#Properties
but this is basically the direction of my question.
(I don’t have currently access to a library, i.e. a book on representation theory.) I mean how do you know that this is a Spin representation with dimension 2ℓ+1 if there is not some concrete construction?
Nad wrote:
Yeah, the theory of spherical harmonics generalizes to any dimension.
I gave one way to do this in my last comment (which I have edited many times, so you may not have read this):
Another nice way is to show that this space Gℓ is isomorphic to the space of degree-ℓ harmonic polynomials on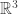 : that is, polynomials that obey Laplace’s equation. Both these tricks are ways of killing off the ‘extra redundant junk’ I discussed in the Postscript, leaving you with just the spin-ℓ rep.
: that is, polynomials that obey Laplace’s equation. Both these tricks are ways of killing off the ‘extra redundant junk’ I discussed in the Postscript, leaving you with just the spin-ℓ rep.
Of course I’m using lots of tricks here. You can also just work everything out using coordinates and lots of explicit calculations! That’s fine too.
The functions of the form [Q^qR^rS^s] don’t actually form a representation of SO(3). They form a basis of the I-invariant functions on the sphere, F^I, but since being I-invariant isn’t preserved under the action of SO(3), F^I doesn’t yield a representation of SO(3).
Rather, what we have is SO(3) acting on the usual three-dimensional space, and thus on polynomials in three variables, call them x, y and z. Since rotation is linear, it sends linear functions to linear functions, and hence doesn’t change the degrees of polynomials. Hence the spaces of homogeneous polynomials in three variables give representations of SO(3).
For me, the easiest way to see that the degree polynomials yield a spin
polynomials yield a spin  representation is to look at the effects of rotations on eigenvectors (if you’re willing to pass into complex stuff). Take u = x + iy, v = x – iy; then
representation is to look at the effects of rotations on eigenvectors (if you’re willing to pass into complex stuff). Take u = x + iy, v = x – iy; then 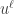 lives in the complexified space of degree
lives in the complexified space of degree  polynomials, and a rotation by t acts on it by
polynomials, and a rotation by t acts on it by 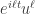 . Hence there is a spin
. Hence there is a spin  representation as a subspace of the homogeneous degree
representation as a subspace of the homogeneous degree  polynomials.
polynomials.
As a subgroup of SO(3), the group I acts on these spaces of homogeneous polynomials. P = P(x,y,z), Q = Q(x,y,z), R = R(x,y,z) and S = S(x,y,z) are all homogeneous polynomials chosen to be invariant under I, and they generate the algebra of I-invariant polynomials in three variables. Restricting to the sphere gives us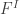 , and then taking associated graded stuff gives us
, and then taking associated graded stuff gives us 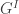 , which are still all I-invariant. But at this point we’ve mostly lost any connection to SO(3).
, which are still all I-invariant. But at this point we’ve mostly lost any connection to SO(3).
Layra wrote:
Right. I never said they did, but I should have been more aggressive in correcting Nad’s impression.
By the way, you used the LaTeX command \script{l}, which doesn’t work here. (Does it work anywhere?) I replaced it with \ell, which is the basic way you make an in LaTeX.
in LaTeX.
I think I might be used to some packages which has a \script command. Not sure.
Depends on what you mean by “form a representation”. As a basis in you can represent a linear transformation on
you can represent a linear transformation on  (i.e a representation in
(i.e a representation in  ) as a matrix in this basis, I would call this a representation is formed in the basis of
) as a matrix in this basis, I would call this a representation is formed in the basis of ![[Q^qR^rS^s]](https://s0.wp.com/latex.php?latex=%5BQ%5EqR%5ErS%5Es%5D&bg=ffffff&fg=333333&s=0&c=20201002) But is this a spin representation? So basically I was asking how concretely the action of SO(3) in
But is this a spin representation? So basically I was asking how concretely the action of SO(3) in ![[Q^qR^rS^s]](https://s0.wp.com/latex.php?latex=%5BQ%5EqR%5ErS%5Es%5D&bg=ffffff&fg=333333&s=0&c=20201002) is defined.
is defined.
I imagine the invariant functions as a “kind of representation” of the set of symmetry axis’ and maybe the set of faces which map onto itself under the symmetries of the polytope. So yes under some arbitray rotations (i.e. not symmetry rotations) these thus get mapped to some other set of axis’ (and faces). But by the above one should still be able to express this collection in the above basis (?). Now since geometric algebras are very losely speaking some way of seeing structured sets of “vectors” as “basis vectors” I had the vague imagination that they appear somewhere here as a means to represent those sets of axis’ and faces. And Greg Egans post now seems to point also in this direction. But as said I just wanted to try to understand all this to at least some rough extend and thus in particular find the right image. And I had hoped that this was easier. I also looked in the wikipedia articles on Spin representations with Clifford algebras or exterior algebras, but I found those not really instructive especially for the above.
So thanks John and Layra for trying to explain the above to me, but I fear this gets a bit too complicated for the limited time I might dedicate to this.
Nad wrote:
As Layra explained, there’s no action of SO(3) on the space spanned by the elements [Q^qR^rS^s]. These are functions invariant under the symmetries of an icosahedron in fixed position. If you rotate such a function, you don’t get another such function.
I never said there was a representation of SO(3) on this space. I used a representation of SO(3) on various other spaces, like the space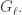
Layra wrote
John wrote:
OK I think I now see what you mean. For me this was not so obvious that if I rotate such a function then that this is not anymore a function in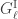 – that may have irritated me.
– that may have irritated me.
Thanks again.
Reducing integers mod , we get a projection of
, we get a projection of  to
to 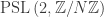 . Now,
. Now, 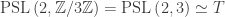 (the rotational symmetry group of the tetrahedron),
(the rotational symmetry group of the tetrahedron), 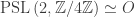 (octahedral rotations) and
(octahedral rotations) and 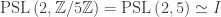 . Likewise for
. Likewise for  we get the symmetries of a tiling of the torus by 12 hexagons; for
we get the symmetries of a tiling of the torus by 12 hexagons; for 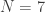 we get the symmetries of the Klein Quartic (with its heptagonal tiling); and so on. So these things presumably do lift to modular functions of level
we get the symmetries of the Klein Quartic (with its heptagonal tiling); and so on. So these things presumably do lift to modular functions of level  .
.
That’s a promising sign! But why should a PSL(2,5)-invariant real-algebraic function on the sphere give a modular function of level 5? We can think of this sphere as the Riemann sphere, and the usual action of the icosahedral group on the sphere gives a complex-algebraic action of PSL(2,5) on the Riemann sphere… but there’s still a gap I don’t see how to fill, between the world of real-algebraic functions and the world of complex-analytic functions.
Maybe I’m not looking at things in the best way. It would be nice to find a connection with modular functions. Maybe I should proceed numerologically and look at some information about modular functions, or forms, at level 5.
Yes, we can think of the sphere as the Riemann sphere… but this story can’t fit inside an SO(3) story, because SO(3) is compact, while the conformal group SL(2,R) is non-compact…
I believe the point is this. The congruence subgroup
acts on the upper half-plane as conformal transformations. The quotient
as conformal transformations. The quotient  is called a modular curve. And the group
is called a modular curve. And the group 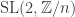 acts as conformal transformations on this modular curve.
acts as conformal transformations on this modular curve.
For the modular curve
the modular curve  can be identified with the Riemann sphere—at least after we compactify it by throwing in a point at infinity. In these three cases the groups
can be identified with the Riemann sphere—at least after we compactify it by throwing in a point at infinity. In these three cases the groups 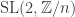 are the binary tetrahedral, binary octahedral and binary icosahedral groups—that is, double covers of the rotational groups of the tetrahedron, octahedron and icosahedron. And they act on the Riemann sphere in a manner that preserves a tetrahedron, octahedron and icosahedron inscribed in this sphere, respectively.
are the binary tetrahedral, binary octahedral and binary icosahedral groups—that is, double covers of the rotational groups of the tetrahedron, octahedron and icosahedron. And they act on the Riemann sphere in a manner that preserves a tetrahedron, octahedron and icosahedron inscribed in this sphere, respectively.
This is the stuff Tim Silverman was alluding to. I think this math goes back to Felix Klein. He then went on to the case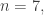 and the rest is history.
and the rest is history.
Well, I was much too hasty! I hadn’t thought of finite subgroups of SL(2,R) which also happen to be finite subgroups of SO(3). This seems like a kind of “coincidence” to me. SO(3) and SL(2,R) have the same dimension but different topology so I’m certainly not going to fine one inside the other. But I hadn’t realized that their finite subgroups intersect! (I know essentially nothing about the finite subgroups of SL(2,R))
Those groups aren’t very interesting. I said the binary tetrahedral, octahedral and icosahedral groups are finite subgroups of SU(2) that are also finite quotient groups of SL(2,Z).
They’re all cyclic groups,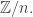
Any finite subgroup of a Lie group G is compact so it must sit inside a maximal compact subgroup K ⊂ G. The existence of a maximal compact subgroup is a nontrivial theorem, but it’s true, and it’s good to learn the maximal compact subgroups of all your favorite Lie groups. For SL(2,R), every maximal compact subgroup is conjugate to SO(2). So, every finite subgroup of SL(2,R) is conjugate to a subgroup of SO(2). So, every finite subgroup of SL(2,R) is a cyclic group!
Argh, so I’m still not reading sufficiently carefully. So to form these binary tetrahedral/octahedral/icosahedral groups, we first reduce from SL(2,R) to SL(2,Z) [fn1], then look at quotient groups? Now I really don’t have intuition for how quotients act on the Riemann sphere. Any pedagogical sources for this?
[fn1] Am I right in saying that SL(2,R) is the group of conformal transformation on the complex plane? But now we’re talking about SL(2,Z) instead—is that just to focus on integer lattices in the complex plane instead?
Right. This is part of a big branch of math called the theory of modular curves. A modular curve is what you get when you take the upper half-plane and mod out by a discrete subgroup of SL(2,R). It’s called a curve because it’s of complex dimension 1. The theory of modular curves is important in number theory: for example, it’s what Wiles used to prove Fermat’s Last Theorem.
I don’t think you can do much better than the blog series by my friend Tim Silverman, who started this discussion. He wrote a bunch of posts, but the first one already gets you to the Platonic solids:
Not quite. The only conformal transformations of the complex plane are translations, rotations and dilations. It’s much better to include a point at infinity and consider the Riemann sphere. SL(2,C) acts as conformal transformations of the Riemann sphere via fractional linear transformations
SL(2,R) is the subgroup that preserves the upper half-plane H. The upper half-plane has a metric making it into the ‘hyperbolic plane’, and SL(2,R) acts as isometries. If you’re a physicist, you want to think of SL(2,R) as the double cover of SO(2,1), which acts on 3d Minkowski spacetime, and the upper half-plane as the hyperboloid
which is naturally a copy of the hyperbolic plane. To get number theory into the game we need to look at SL(2,Z) and its congruence subgroups like the groups Γ(n) that I was just talking about.
Great post and thread! Anyone happens being able to explain the relation between icosahedral symmetry and “natural numbers that cannot be expressed as sum of one or more nontrivial binomial coefficients.”? As a matter of fact this is the description of the finite sequence 1, 2, 3, 4, 5, 7, 8, 9, 11, 13, 14, 17, 19, 23, 29 in OEIS (https://oeis.org/A210576).
That’s a nice observation. I think I understand it. From the icosahedral point of view, the important thing about this list of numbers is that they’re the natural numbers that can’t be written as a sum of 6’s, 10’s and 15’s. Our study of the icosahedron, explained in this post, revealed the importance of the numbers 6, 10 and 15.
On the other hand, 6, 10 and 15 are the first 3 nontrivial binomial coefficients. And it just so happens that any number that can’t be written as a sum of these can’t be written as a sum of nontrivial binomial coefficients at all!
This is pretty easy to see. The next binomial coefficient, 21, doesn’t help get you new sums because 21 = 6 + 15. The one after that, 28, doesn’t help get you new sums because 28 = 6 + 6 + 6 + 10. And all the binomial coefficients after that don’t help at all because they’re bigger than 30, and every number greater than or equal to 30 is a sum of 6’s, 10’s, and 15’s.
(In fact you only need to use at most one 15 in this sum.)
All this reminds me of another interesting property of the number 30. It’s the largest natural number such that all natural numbers smaller than it and relatively prime to it are actually prime—except, of course, for 1:
7, 11, 13, 17, 19, 23, 29
This list is contained in your list. I don’t see any significance except that the niceness of the icosahedron is closely connected to it having a very ’round’ number of rotational symmetries, namely 60. The Babylonians liked this number because it was divisible by 2, 3, 5 and even 12… so of course sadistic Babylonian school-teachers gave homework where students had to divide by 7. (A tablet has been found with this homework problem on it.)
Makes sense, thank you! One is tempted to tell OEIS about the alternative description of A210576 as “Numbers that are no sums of 6,10 and 15.”, but then it’s a short list, so maybe its not too big a thing that it can be defined in various short ways.
Wow! Layra has cracked the general proplem of which we were doing special cases:
• Layra Idarani, SG-invariant polynomials.
Namely, he takes any Coxeter group acting on its vector space
acting on its vector space  and answers this puzzle:
and answers this puzzle:
Puzzle. What’s the dimension of the space homogeneous harmonic polynomials of degree on
on  that are invariant under the even part of
that are invariant under the even part of 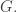
Answer. Any Coxeter group has a list of numbers associated to it, and the answer to the puzzle is how many ways you can write
associated to it, and the answer to the puzzle is how many ways you can write  as an unordered sum of
as an unordered sum of 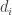 s for
s for 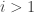 and at most one copy of
and at most one copy of
These lists of numbers associated to Coxeter groups are explained in week186 and week187, but Layra says what these lists are. For the symmetry group of the icosahedron the list is
2, 6, 10
so the answer to the puzzle is: the number of ways we can write as a sum of 6s, 10s and at most one 15. Which is what we’d already seen!
as a sum of 6s, 10s and at most one 15. Which is what we’d already seen!
But the list for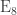 is
is
2, 8, 12, 14, 18, 20, 24, 30
so we can now do this case as well. The dimension of the space of degree- harmonic polynomials on
harmonic polynomials on  that are invariant under the even part of the Weyl group of
that are invariant under the even part of the Weyl group of 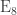 is the number of ways you can write
is the number of ways you can write  as an unordered sum of 2s, 8s, 12s, 14s, 18s, 20s, 24s, 30s and at most one 120.
as an unordered sum of 2s, 8s, 12s, 14s, 18s, 20s, 24s, 30s and at most one 120.
Layra Idarani has come up with a complete classification of all eigenfunctions of the Laplacian on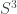 that are invariant under this group… or more generally, eigenfunctions of the Laplacian on a sphere of any dimension that are invariant under the even part of any Coxeter group. For the details, go here:
that are invariant under this group… or more generally, eigenfunctions of the Laplacian on a sphere of any dimension that are invariant under the even part of any Coxeter group. For the details, go here:
• Layra Idarani, SG-invariant polynomials, 4 January 2018.
All that is a continuation of a story whose beginning is summarized here:
• John Baez, Quantum mechanics and the dodecahedron.
So, there’s a lot of serious math under the hood. But right now I just want to marvel at the fact that we’ve found a wavefunction for the hydrogen atom that not only has a well-defined energy, but is also invariant under this 7,200-element group. This group includes the usual 60 rotational symmetries of a dodecahedron, but also other much less obvious symmetries.
Thanks for this post; it helped me with my work, which I was looking forward to sharing here. We develop quantum error-correcting codes for the rigid rotor and its relatives. H-symmetric harmonics are one of our tools, and we obtain them by symmetrizing the ordinary harmonics (be it for or the two-sphere) over the group H. I’m sure this isn’t new, but haven’t quite seen it spelled out the same way. We also formulate a “coordinates statement” of Peter-Weyl on homogeneous spaces. I would be interested in comments and any refs I missed! https://scirate.com/arxiv/1911.00099
or the two-sphere) over the group H. I’m sure this isn’t new, but haven’t quite seen it spelled out the same way. We also formulate a “coordinates statement” of Peter-Weyl on homogeneous spaces. I would be interested in comments and any refs I missed! https://scirate.com/arxiv/1911.00099
I’m busy grading midterms and preparing for classes but I hope someday I have time to look at your paper!
Thanks for the interest! The math-related part is Appx. D. I don’t think it’s at all surprising one can formulate a “grand orthogonality theorem” for coset spaces, but I’ve never seen it explicitly written either. If you’re interested in the quantum aspects, feel free to read my blog post: https://quantumfrontiers.com/2019/11/17/on-the-coattails-of-quantum-supremacy/
Interesting (and long) paper! Never got in touch with quantum computing before but to me it seems to be closely related to microwave spectroscopy and theoretical chemistry, though the language is a physics/maths one ( versus
versus  , …).
, …).
The paper tries to push quantum computing in the direction of rotational state spaces, which have been thoroughly studied in spectroscopy. I try to include all the jargon for the groups in the text to make it easier ( and $latex $C_\infty = SO(2)=U(1)$).
and $latex $C_\infty = SO(2)=U(1)$).
This a very good idea, I am sure it will help attracting more interest from people with knowledge on spectroscopy!
P.S.: Strange, I must have posted this about one year ago (at leat quite a few months) or so. The timeline thoroughly confuses (if not scares) me ..
We could also define A5 as the group of rotations which fix the following degree-6 polynomial (x − φy)(y − φz)(z − φx)(x + φy)(y + φz)(z + φx), which is isomorphic to Greg Egan’s potential function discussed here. This is mildly (but not precisely*) analogous to the description of the Monster as the automorphisms of the Griess algebra. Note that the polynomial is clearly invariant under the monomial subgroup A4, and with some effort can be shown to be invariant under the full group A5.
Hi John Baez
Thank you for that post! It means a lot to me. If you consider the possibility of magnesium (12!) to form the dodecahedron configuration, then we could reach a break through in the understanding of photosynthesis. Its crystal like structures (chlorophyll esp. porphyrin ring) transform the molecules “vibrations” (chaotic movements) to 3d symmetrical impacts on magnesium by four nitrogen atoms with three free valence electrons each.
I know the conflict with Paulis exclusion principle, but I am considering nature to be smart enough to find a way around it. Superposition??
(Sorry, I’m an engineer not mathematician nor physicist and therefore cannot follow or use your formal language, but I am working on the same question in a more practical approach.)
Life has to use the ideal distribution of energy in order to overcome the spontaneous processes. In the end almost all living creatures gain their energy for the most part from photosynthesis. The solution to that seems to me to be Platos and Keplers dodecahedron representing the “aether”: the most dense symmetric form of energy. You just have to align the electrons to it. By doing so, you transform “vibrational” energy to spin energy. Photosynthesis does this with magnesium in a quasi crystal structure (just with one atom) what can be done by men creating superconductors.
Is that comprehensible for you?