Johannes Kepler loved geometry, so of course he was fascinated by Platonic solids. His early work Mysterium Cosmographicum, written in 1596, includes pictures showing how the 5 Platonic solids correspond to the 5 elements:
Five elements? Yes, besides earth, air, water and fire, he includes a fifth element that doesn’t feel the Earth’s gravitational pull: the ‘quintessence’, or ‘aether’, from which heavenly bodies are made.
In the same book he also tried to use the Platonic solids to explain the orbits of the planets:
The six planets are Mercury, Venus, Earth, Mars, Jupiter and Saturn. And the tetrahedron and cube, in case you’re wondering, sit outside the largest sphere shown above. You can see them another picture from Kepler’s book:
These ideas may seem goofy now, but studying the exact radii of the planets’ orbits led him to discover that these orbits aren’t circular: they’re ellipses! By 1619 this led him to what we call Kepler’s laws of planetary motion. And those, in turn, helped Newton verify Hooke’s hunch that the force of gravity goes as the inverse square of the distance between bodies!
In honor of this, the problem of a particle orbiting in an inverse square force law is called the Kepler problem.
So, I’m happy that Greg Egan, Layra Idarani and I have come across a solid mathematical connection between the Platonic solids and the Kepler problem.
But this involves a detour into the 4th dimension!
It’s a remarkable fact that the Kepler problem has not just the expected conserved quantities—energy and the 3 components of angular momentum—but also 3 more: the components of the Runge–Lenz vector. To understand those extra conserved quantities, go here:
• Greg Egan, The ellipse and the atom.
Noether proved that conserved quantities come from symmetries. Energy comes from time translation symmetry. Angular momentum comes from rotation symmetry. Since the group of rotations in 3 dimensions, called SO(3), is itself 3-dimensional, it gives 3 conserved quantities, which are the 3 components of angular momentum.
None of this is really surprising. But if we take the angular momentum together with the Runge–Lenz vector, we get 6 conserved quantities—and these turn out to come from the group of rotations in 4 dimensions, SO(4), which is itself 6-dimensional. The obvious symmetries in this group just rotate a planet’s elliptical orbit, while the unobvious ones can also squash or stretch it, changing the eccentricity of the orbit.
(To be precise, all this is true only for the ‘bound states’ of the Kepler problem: the circular and elliptical orbits, not the parabolic or hyperbolic ones, which work in a somewhat different way. I’ll only be talking about bound states in this post!)
Why should the Kepler problem have symmetries coming from rotations in 4 dimensions? This is a fascinating puzzle—we know a lot about it, but I doubt the last word has been spoken. For an overview, go here:
• John Baez, Mysteries of the gravitational 2-body problem.
This SO(4) symmetry applies not only to the classical mechanics of the inverse square force law, but also the quantum mechanics! Nobody cares much about the quantum mechanics of two particles attracting gravitationally via an inverse square force law—but people care a lot about the quantum mechanics of hydrogen atoms, where the electron and proton attract each other via their electric field, which also obeys an inverse square force law.
So, let’s talk about hydrogen. And to keep things simple, let’s pretend the proton stays fixed while the electron orbits it. This is a pretty good approximation, and experts will know how to do things exactly right. It requires only a slight correction.
It turns out that wavefunctions for bound states of hydrogen can be reinterpreted as functions on the 3-sphere, S3 The sneaky SO(4) symmetry then becomes obvious: it just rotates this sphere! And the Hamiltonian of the hydrogen atom is closely connected to the Laplacian on the 3-sphere. The Laplacian has eigenspaces of dimensions n2 where n = 1,2,3,…, and these correspond to the eigenspaces of the hydrogen atom Hamiltonian. The number n is called the principal quantum number, and the hydrogen atom’s energy is proportional to -1/n2.
If you don’t know all this jargon, don’t worry! All you need to know is this: if we find an eigenfunction of the Laplacian on the 3-sphere, it will give a state where the hydrogen atom has a definite energy. And if this eigenfunction is invariant under some subgroup of SO(4), so will this state of the hydrogen atom!
The biggest finite subgroup of SO(4) is the rotational symmetry group of the 600-cell, a wonderful 4-dimensional shape with 120 vertices and 600 dodecahedral faces. The rotational symmetry group of this shape has a whopping 7,200 elements! And here is a marvelous moving image, made by Greg Egan, of an eigenfunction of the Laplacian on S3 that’s invariant under this 7,200-element group:

We’re seeing the wavefunction on a moving slice of the 3-sphere, which is a 2-sphere. This wavefunction is actually real-valued. Blue regions are where this function is positive, yellow regions where it’s negative—or maybe the other way around—and black is where it’s almost zero. When the image fades to black, our moving slice is passing through a 2-sphere where the wavefunction is almost zero.
Layra Idarani came up with a complete classification of all eigenfunctions of the Laplacian on S3 that are invariant under this group… or more generally, eigenfunctions of the Laplacian on a sphere of any dimension that are invariant under the even part of any Coxeter group. Unfortunately he posted it to Google+, so it may be lost now. If you can find it, let me know!
Right now, the best place to look for more information—and pictures—is here:
• Greg Egan, Symmetric waves.
All that is a continuation of a story whose beginning is summarized here:
• John Baez, Quantum mechanics and the dodecahedron.
So, there’s a lot of serious math under the hood. But right now I just want to marvel at the fact that we’ve found a wavefunction for the hydrogen atom that not only has a well-defined energy, but is also invariant under this 7,200-element group. This group includes the usual 60 rotational symmetries of a dodecahedron, but also other much less obvious symmetries.
I don’t have a good picture of what these less obvious symmetries do to the wavefunction of a hydrogen atom. I understand them a bit better classically—where, as I said, they squash or stretch an elliptical orbit, changing its eccentricity while not changing its energy.
We can have fun with this using the old quantum theory—the approach to quantum mechanics that Bohr developed with his colleague Sommerfeld from 1920 to 1925, before Schrödinger introduced wavefunctions.
In the old Bohr–Sommerfeld approach to the hydrogen atom, the quantum states with specified energy, total angular momentum and angular momentum about a fixed axis were drawn as elliptical orbits. In this approach, the symmetries that squash or stretch elliptical orbits are a bit easier to visualize:
This picture by Pieter Kuiper shows some orbits at the 5th energy level, n = 5: namely, those with different eigenvalues of the total angular momentum, ℓ.
While the old quantum theory was superseded by the approach using wavefunctions, it’s possible to make it mathematically rigorous for the hydrogen atom. So, we can draw elliptical orbits that rigorously correspond to a basis of wavefunctions for the hydrogen atom. So, I believe we can draw the orbits corresponding to the basis elements whose linear combination gives the wavefunction shown as a function on the 3-sphere in Greg’s picture above!
We should get a bunch of ellipses forming a complicated picture with dodecahedral symmetry. This would make Kepler happy.
As a first step in this direction, Greg drew the collection of orbits that results when we take a circle and apply all the symmetries of the 600-cell:

Postscript
To do this really right, one should learn a bit about ‘old quantum theory’. I believe people have been getting it a bit wrong for quite a while—starting with Bohr and Sommerfeld!
If you look at the ℓ = 0 orbit in the picture above, it’s a long skinny ellipse. But I believe it really should be a line segment straight through the proton: that’s what’s an orbit with no angular momentum looks like.
There’s a paper about this:
• Manfred Bucher, Rise and fall of the old quantum theory.
Matt McIrvin had some comments on this:
This paper from 2008 is a kind of thing I really like: an exploration of an old, incomplete theory that takes it further than anyone actually did at the time.
It has to do with the Bohr-Sommerfeld “old quantum theory”, in which electrons followed definite orbits in the atom, but these were quantized–not all orbits were permitted. Bohr managed to derive the hydrogen spectrum by assuming circular orbits, then Sommerfeld did much more by extending the theory to elliptical orbits with various shapes and orientations. But there were some problems that proved maddeningly intractable with this analysis, and it eventually led to the abandonment of the “orbit paradigm” in favor of Heisenberg’s matrix mechanics and Schrödinger’s wave mechanics, what we know as modern quantum theory.
The paper argues that the old quantum theory was abandoned prematurely. Many of the problems Bohr and Sommerfeld had came not from the orbit paradigm per se, but from a much simpler bug in the theory: namely, their rejection of orbits in which the electron moves entirely radially and goes right through the nucleus! Sommerfeld called these orbits “unphysical”, but they actually correspond to the s orbital states in the full quantum theory, with zero angular momentum. And, of course, in the full theory the electron in these states does have some probability of being inside the nucleus.
So Sommerfeld’s orbital angular momenta were always off by one unit. The hydrogen spectrum came out right anyway because of the happy accident of the energy degeneracy of certain orbits in the Coulomb potential.
I guess the states they really should have been rejecting as “unphysical” were Bohr’s circular orbits: no radial motion would correspond to a certain zero radial momentum in the full theory, and we can’t have that for a confined electron because of the uncertainty principle.





One could wish that element-based names (pyromorph, aeromorph …) had caught on for the Platonic solids, rather than number-names; analogous names for the 4-polytopes would be easier on the tongue than hecatonicosichoron. (For the 24-cell, which has no good 3-space analogue, I’d borrow wood from the Chinese elements.)
Moreover, I think the following reference deserves attention: “Algebraic Solution to the Kepler Problem”, Am. J. of Physics, 38, n2, February 1970, pages 253 to 255, by P. Collas.
Thanks!
You’re welcome…By the way, have a look on Nikitin’s papers https://arxiv.org/abs/1308.4279 , https://arxiv.org/abs/1403.2867 and Gibbons et al. https://arxiv.org/abs/1404.3422 That’s all what I can do at the moment…
(It seems this post was not duplicated, I belibe) Great piece of you again, John C. Baez! I have written about the Bohr model in my blog copiously. Indeed, the Bohr model is a nice toy model (even when incorrect!) for many simple problems. Even you can use it to reproduce easily the Dirac quantization condition on magnetic monopoles! I have not written all what I would like to write about it! And hidden symmetries like this article are nice to read. ALWAYS! In fact, in relativistic gravity (general relativity) we lack something like this toy model due to the details of the theory BUT, not everything has been sais as…The Kerr metric has a hidden symmetry due to the Killing vector producing the Carter Constant!!!!!! As far as I know, no hyperdimensional interpretation of the Carter constant has been done (not sure if it even exists!). I am trying to program the kerr orbits (triperiodic!!!!!) for my second master degree and it is a hard task, but I have been reading on hidden symmetries in general relativity, and it is perturbing how much do we ignore about the origin (geometry) of the Carter constant and/or the now moody asymptotic symmetries in black hole (likely related to the information paradox solution!). There is another curious story I was told in my first Master degree. If you write up the equations for a vector-like theory of gravity, the ellipses and the precesion of Mercury give a wrong result (beyond the fact vector gravity produces a repulsive force!!!!). Said this, again, thank you to share your 600-cell math knowledge with the Kepler link with us. May the Kepler be with you!
According to Wikipedia it seems Kepler speeded up finishing his work
“Harmonices Mundi” (which apparently contained amongst others the third law of planetary motion) during the witch trial of his mother:
That is he was already sufficiently in trouble with the church himself like
so maybe he feared that he might not survive his attempt to prevent his mothers immolation..
There is a whole book on the Kepler problem by Bruno Caprani, who showed (based on other work) that the symmetry group of hydrogen (or the 2-body problem) is in fact the conformal group SO(4,2). It contains your groups SO(4), SO(3,1), and ISO(3) as subgroups.
I should read that book. Unless I’m seriously confused, SO(4,2) arises a ‘dynamical’ symmetry group—not all transformations in that group commute with the Hamiltonian. This is fairly easy to see, since the eigenspaces of the Hamiltonian for the bound states are finite-dimensional, and SO(4,2) doesn’t have enough nontrivial finite-dimensional unitary representations to act unitarily on these eigenspaces.
I’ve collected a large list of references on the Kepler problem here, not all of which I’ve read yet:
• Mysteries of the gravitational 2-body problem.
But Caprani’s book is not in there, so I’ll have to add it.
Arnold wrote:
I’m not finding any traces of such a book on Google.
Sorry, spelling mistake. The book is by Bruno Cordani, http://www.springer.com/de/book/9783764369026
Yes, SO(4,2) is a dynamical symmetry group. This is the right group to study the hydrogen atom, as the Lie algebra so(4,2) contains a full set of generators for its phase space Poisson algebra.
Thanks, I’ll check it out. I did my PhD thesis on 4d conformally invariant quantum field theories, where the symmetry group is SO(4,2) or its double cover SU(2,2). I focused on the relatively simple-minded linear theories like Maxwell’s equations and the wave equation These give unitary representations of SU(2,2). I’ll enjoy thinking about the Kepler problem using SO(4,2). Do you recall if this has a unitary representation on the Hilbert space for a hydrogen atom?
These give unitary representations of SU(2,2). I’ll enjoy thinking about the Kepler problem using SO(4,2). Do you recall if this has a unitary representation on the Hilbert space for a hydrogen atom?
Yes it has. It corresponds to the the most degenerate unitary representation of SU(2,2). It is obtainable, e.g., by geometric quantization of SO(4,2), using the Kähler structure of the Hermitian symmetric space of type , which is the (completed at
, which is the (completed at  ) classical phase space of the Kepler problem, on which SO(4,2) acts. This gives an associated coherent state representation, which should be a neat way to study the quantum-classical correspondence between the hydrogen atom and the Kepler problem.
) classical phase space of the Kepler problem, on which SO(4,2) acts. This gives an associated coherent state representation, which should be a neat way to study the quantum-classical correspondence between the hydrogen atom and the Kepler problem.
I’d like to have (i) an explicit formula (without integrals!) for the inner product of two states in one of the nice parameterizations of the symmetric space, (ii) an explicit description of how SO(4,2) [not SU(2,2), which needs an awkward transformation to get to the nice geometric features] acts in this parameterization projectively on the corresponding line bundle, and (iii) a formula representing these coherent states in some Hilbert space, from which the formula for the inner product can be obtained in a simple way. I am sure all this is possible!
But I have not yet been successful in finding it. It would make a nice paper. There are multiple accounts of the representation in the literature, but none of them that would satisfy me. The main problem is that none of the more explicit descriptions available seems to be free of subtle copying errors, and figuring out which formulas are reliable is awkward. I tried at various times and wasted a lot of time on this.
Maybe you with your sense of beauty will be able to solve my quest! I’d be happy to share with you (offline) partial results that I already have, and notes on pitfalls in the literature.
This sounds like a great thing to ponder! It’ll take me a while to get going, since I’m teaching a bunch of classes this quarter. But I think it could connect very nicely with the Bohr–Sommerfeld quantization of the hydrogen atom, which itself a different form of geometric quantization, based on a Lagrangian rather than Kähler polarization.
Just to put the problem into my brain, so I can start pondering it in my spare moments, could you tell me what subgroup H ⊂ SO(2,4) we should use, for SO(2,4)/H to be this symmetric space?
When I get a bit more time I’ll email you… or you can email me whenever you want.
B. Cordani,
Quantization of the Kepler Manifold,
Commun. Math. Phys. 113 (1988), 649–657.
describes the point stabilizer on p. 651, so that
on p. 651, so that  is the Kepler manifold.
is the Kepler manifold.
Thanks! I’m reading Cordani’s book; I guess this information must also be there, but I haven’t seen it yet.
I see now that what I really need is not just this stabilizer, but an intuitive understanding of the connection between the group SO(2,4) and the Kepler manifold.
For people just listening in: the Kepler manifold is the cotangent bundle of the 3-sphere with the zero covectors removed. Points in here correspond to negative-energy states of a particle in an attractive inverse square force.
is the cotangent bundle of the 3-sphere with the zero covectors removed. Points in here correspond to negative-energy states of a particle in an attractive inverse square force.
Cordani explains a way that SO(2,4) acts on this space. He does it using conformally compactified Minkowski spacetime
which is something I like. But I need to to get more of an intuition of what’s going on! When I can picture things in my head, I can usually make rapid progress. I’m not at that stage yet.
Right this moment I’m stuck on something embarrassingly simple. I’ll explain it publicly just to keep the conversation going, though I should probably figure it out myself. Theorem 6.9 of Cordani’s book seems to say that is diffeomorphic (even symplectomorphic) to the manifold of future-pointing null covectors in
is diffeomorphic (even symplectomorphic) to the manifold of future-pointing null covectors in  . But
. But 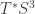 is 6-dimensional and the space of future-pointing null covectors in
is 6-dimensional and the space of future-pointing null covectors in  is 7-dimensional!
is 7-dimensional!
Did Cordani mean to take the manifold of future-pointing null covectors in and fiberwise projectivize it, reducing its dimension by one? Am I misreading something? If I can’t get this right, I can’t trust myself… and if he can’t get it right I can’t trust him.
and fiberwise projectivize it, reducing its dimension by one? Am I misreading something? If I can’t get this right, I can’t trust myself… and if he can’t get it right I can’t trust him.
Cordani extends in his paper
Conformal regularization of the Kepler problem,
Commun. Math. Phys. 103 (1986), 403-413.
the 6D phase space to an 8D extended phase space (which also contains energy and time as conjugate variables), and then restricts the action [before (1.5) there] to an orbit, which is 7D.
That’s very interesting, and it might be the right way to go about things, but I really want to know whether Cordani’s book has a serious mistake, or whether I’m seriously confused. He seems to say quite clearly that is symplectomorphic to the space of future-pointing null covectors in conformally compactified (n+1)-dimensional Minkowski spacetime. I think this is impossible, since these manifolds are of different dimension. Am I wrong?
is symplectomorphic to the space of future-pointing null covectors in conformally compactified (n+1)-dimensional Minkowski spacetime. I think this is impossible, since these manifolds are of different dimension. Am I wrong?
The book seems to have appeared after the paper you mention, so it’s not as if the paper corrects a mistake in the book.
Okay, I think I have this figured out. More later.
I am thinking if it were possible to write an Hamiltonian for each symmetry group, which had all the wave functions with a given symmetry.
If the canonical commutations formed a group (that is the symmetry group), using operators that commute with the Hamiltonian, then the wave functions would have the same symmetries (using the canonical commutations rules for products of constants of motion).
I’m thinking that if the Hamiltonian commute with two angular moments, M and N, where N is at a small angle from M, then any product of the moments is a constant of motion for the wave function, using the commutator rules ; this is true if there is a Hamiltonian who commutes with two angular moments that are non-orthogonal
The first steps toward drawing the Bohr–Sommerfeld picture of a hydrogen energy eigenstate with symmetry under a large subgroup of SO(4) are to:
1) Figure out which elliptical orbits correspond to the quantum states with given (n,ℓ,m) in the Bohr–Sommerfeld picture. This is explained here:
• Manfred Bucher, Rise and fall of the old quantum theory.
where I believe Bucher has corrected a small but important mistake in the work of Bohr and Sommerfeld.
2) Figure out how SO(4) acts on the space of elliptical orbits. Some relevant material is here:
• Greg Egan, The ellipse and the atom.
However, this mainly talks about an orbit not as an ellipse in position space but as a circle in momentum space. That’s very beautiful, but to see how SO(4) acts on ellipses it may be good to use the idea here:
• John Baez, Planets in the 4th dimension.
The idea is to treat all elliptical orbits with a given energy, hence a given semimajor axis a, as great circles on a fixed 3-sphere of radius a. Dropping down one dimension, the picture looks like this:
I could be mixed up, but I think the action of SO(4) on the set of elliptical orbits of the given energy then comes from the obvious action on rotations on this 3-sphere. However, this gives a bunch of ellipses with the same center, and then one has to translate them to get a bunch of ellipses with the same focuse.
I am thinking that it is possible to write a class of high degree and high order differential equation with solutions that have the symmetries of each group.
If a differential equation have N free parameters, then it is possible to obtain for each transformation in the group a constraint on the parameters, that could be solved using a minimization with gradient descent (or other optimization algorithm) whatever the complexity of the constraint; if the differential equation is the Schrodinger equation, with a polynomial potential with N free parameters, then it is possible to obtain a class of wave function with the symmetries of the group, in the three dimensional space and only for some groups.
I am confused. How does this 4-dimensional, SO(4)-style treatment of the hydrogen atom relate to the usual undergraduate treatment in terms of spherical harmonics on ?
?
The basic idea is this: the bound states of hydrogen with a given energy form a reducible representation of SO(3) which is all we see from the usual spherical harmonic story. But they form an irreducible representation of SO(4). Thus, this extra symmetry explains why we have so many states with the same energy—more than can be explained using SO(3) symmetry!
Here’s a quick sketch of how it works.
SO(3) story. As a representation of SO(3) we have
where![[j]](https://s0.wp.com/latex.php?latex=%5Bj%5D&bg=ffffff&fg=333333&s=0&c=20201002) is the spin-j representation of SO(3). This is the usual decomposition of functions on the sphere into spherical harmonics, expressed in a less grungy manner: spherical harmonics give explicit bases for the irreps
is the spin-j representation of SO(3). This is the usual decomposition of functions on the sphere into spherical harmonics, expressed in a less grungy manner: spherical harmonics give explicit bases for the irreps ![[j] \subset L^2(S^2).](https://s0.wp.com/latex.php?latex=%5Bj%5D+%5Csubset+L%5E2%28S%5E2%29.&bg=ffffff&fg=333333&s=0&c=20201002)
The space of hydrogen atom bound states at the th energy level is isomorphic to
th energy level is isomorphic to
if we call the lowest energy level the 0th energy level, which is not standard (people usually call it the first). Thus, a basis of bound states is indexed by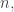 another number called
another number called  saying which irrep
saying which irrep ![[0], \dots, [n]](https://s0.wp.com/latex.php?latex=%5B0%5D%2C+%5Cdots%2C+%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) we’re in, and a third number called
we’re in, and a third number called  indexing a basis of this irrep. These numbers
indexing a basis of this irrep. These numbers  are the usual quantum numbers for the electron in the quantum number, except that my
are the usual quantum numbers for the electron in the quantum number, except that my  is one less than the usual convention.
is one less than the usual convention.
These energy eigenstates are functions on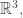 but we can restrict them to functions on the sphere, giving
but we can restrict them to functions on the sphere, giving
SO(4) story. On the other hand, the space of all bound states of the hydrogen atom is naturally a representation not only of but also
but also  , and thus of the double cover
, and thus of the double cover  . Since
. Since 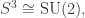 the Peter–Weyl theorem says
the Peter–Weyl theorem says
as representations of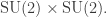 The states in the
The states in the  th energy level form the subspace
th energy level form the subspace ![[j] \otimes [j]](https://s0.wp.com/latex.php?latex=%5Bj%5D+%5Cotimes+%5Bj%5D&bg=ffffff&fg=333333&s=0&c=20201002) where
where  The
The  from the previous story is covered by the diagonal subgroup of
from the previous story is covered by the diagonal subgroup of 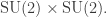
To check the consistency of the two stories, note that perfect squares are sums of odd numbers:
where and
and  So, the energy eigenspace
So, the energy eigenspace
from the first story at least has the same dimension as the energy eigenspace
from the second story. But in fact they’re isomorphic as representations of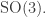 And indeed, this energy eigenspace is an irrep of
And indeed, this energy eigenspace is an irrep of  So, we’re seeing how an irrep of
So, we’re seeing how an irrep of  decomposes as irreps of
decomposes as irreps of 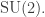
It’s nice that this math gives a pretty good approximate description of the most common element in the Universe. When asked if there were anything that could be concluded about God from the study of natural history, Haldane said “He has an inordinate fondness for beetles”. But there are a lot more hydrogen atoms.
Thanks for this beautiful summary.
Thanks! There’s a lot more I want to say by now; I guess it’s time to write another episode of this thread.
Yes, please – and please announce it here so that I am informed…
Believe it or not, I’ve been continuing to think about some of the things we discussed. However, my first batch of comments will only discuss the bound states, not all the states of the hydrogen atom.
There is something I don’t understand. How do we explicitly make the transition from the quantum mechanics Hilbert space to
to  ? Is it stereographic projection? How do we understand this physically?
? Is it stereographic projection? How do we understand this physically?
Also, have you seen the book “Variations on a Theme by Kepler” by Guillemin and Sternberg on this material?
I spent about 3 months carefully reading Variations on a Theme by Kepler. They discuss the map at the classical level, and that’s probably the best way to get an intuition for the quantum map.
at the classical level, and that’s probably the best way to get an intuition for the quantum map.
I reached my maximal point of understanding this stuff shortly after giving this talk at Georgia Tech in March 2019:
• Hidden symmetries of the hydrogen atom.
But I haven’t thought about this since April, and right now my brain is full of combinatorial species and Hopf algebras, so it would be quite painful for me to suddenly try to remember what I was thinking about the hydrogen atom well enough to explain it. Someday I want to explain it and wow the world with some new discoveries… but today is not that day. For now I recommend Variations on a Theme by Kepler and also
• Bruno Cordani, The Kepler Problem: Group Theoretical Aspects, Regularization and Quantization, with Application to the Study of Pertubation, Birkhäuser, Boston, 2002.
Taken together they explain this quite well. But it’s a bit confusing because there are several interlocking viewpoints, and at first it’s hard to believe they’re all true.
Also, if you haven’t read my talk slides, you might try, since they’re about as good as anything I’d say off the cuff right now.
Ok, thanks for the extra reference. I have read your slides already, naturally. I’ve also looked at Greg Egan’s page, and the reference he gives by Jonas Karlsson, “The SO(4) symmetry of the hydrogen atom” which I also found very helpful.
I found this interesting reference when searching a link between SO(4,2) and supersymmetry in bibliography: https://www.sciencedirect.com/science/article/pii/0550321385903116?via%3Dihub
It looks like the links for SO(3) and SO(4) both go to the Wikipedia page about SO(4).
Fixed! What made you read this blog article just now, Blake? I’ve been planning to get back to work on the Kepler problem, but you seem to have picked that up telepathically.
The little gadget on the website that shows a few random past posts served this up to me, and I figured I’d give it a re-read. I’ve also been planning to return to the Kepler problem, or rather, the quantum Coulomb problem. I have a heap of old notes on the topic that I need to do something with, even if it’s only to get them into shape to put on the arXiv as a pedagogical piece for students.
I’ve been planning a round of exposition/research on both the classical and quantum Kepler problems myself, so if you write something I’d like to look at it!