Back in 2015, I reported some progress on this difficult problem in plane geometry. I’m happy to report some more.
First, remember the story. A subset of the plane has diameter 1 if the distance between any two points in this set is ≤ 1. A universal covering is a convex subset of the plane that can cover a translated, reflected and/or rotated version of every subset of the plane with diameter 1. In 1914, the famous mathematician Henri Lebesgue sent a letter to a fellow named Pál, challenging him to find the universal covering with the least area.
Pál worked on this problem, and 6 years later he published a paper on it. He found a very nice universal covering: a regular hexagon in which one can inscribe a circle of diameter 1. This has area
But he also found a universal covering with less area, by removing two triangles from this hexagon—for example, the triangles C1C2C3 and E1E2E3 here:
The resulting universal covering has area
In 1936, Sprague went on to prove that more area could be removed from another corner of Pál’s original hexagon, giving a universal covering of area
In 1992, Hansen took these reductions even further by removing two more pieces from Pál’s hexagon. Each piece is a thin sliver bounded by two straight lines and an arc. The first piece is tiny. The second is downright microscopic!
Hansen claimed the areas of these regions were 4 · 10-11 and 6 · 10-18. This turned out to be wrong. The actual areas are 3.7507 · 10-11 and 8.4460 · 10-21. The resulting universal covering had an area of
This tiny improvement over Sprague’s work led Klee and Wagon to write:
it does seem safe to guess that progress on [this problem], which has been painfully slow in the past, may be even more painfully slow in the future.
However, in 2015 Philip Gibbs found a way to remove about a million times more area than Hansen’s larger region: a whopping 2.233 · 10-5. This gave a universal covering with area
Karine Bagdasaryan and I helped Gibbs write up a rigorous proof of this result, and we published it here:
• John Baez, Karine Bagdasaryan and Philip Gibbs, The Lebesgue universal covering problem, Journal of Computational Geometry 6 (2015), 288–299.
Greg Egan played an instrumental role as well, catching various computational errors.
At the time Philip was sure he could remove even more area, at the expense of a more complicated proof. Since the proof was already quite complicated, we decided to stick with what we had.
But this week I met Philip at The philosophy and physics of Noether’s theorems, a wonderful workshop in London which deserves a full blog article of its own. It turns out that he has gone further: he claims to have found a vastly better universal covering, with area
This is an improvement of 2.178245 × 10-5 over our earlier work—roughly equal to our improvement over Hansen.
You can read his argument here:
• Philip Gibbs, An upper bound for Lebesgue’s universal covering problem, 22 January 2018.
I say ‘claims’ not because I doubt his result—he’s clearly a master at this kind of mathematics!—but because I haven’t checked it and it’s easy to make mistakes, for example mistakes in computing the areas of the shapes removed.
It seems we are closing in on the final result; however, Philip Gibbs believes there is still room for improvement, so I expect it will take at least a decade or two to solve this problem… unless, of course, some mathematicians start working on it full-time, which could speed things up considerably.
Azimuth 
Suppose someone found an optimal universal covering — does anyone have a plausible scheme for proving it optimal?
People know how to get upper bounds using arguments like those constructed by the people listed in this post. People know how to get lower bounds by showing that any shape that contains all shapes of certain kinds must have at least some area. In theory these arguments could meet! In practice, they seem to be creeping closer and closer, but with a gap much bigger than the latest improvements.
The current upper bound, if Philip’s new paper is correct, is
This is roughly 0.00002 less than the previous upper bound.
On the other hand, the best known lower bound I know is due to Brass and Sharifi in 2005. They got a lower bound of
This is 0.0049 higher than the previous lower bound.
I think people haven’t put as much work into lower bounds, so I think the main reason for the gap is that the lower bounds aren’t big enough… not that the upper bounds are too big, though Philip is sure someone could bring them down with further work.
I seem to recall proving by a rather abstract argument that the actual constant we’re closing in on is effectively computable. (I never wrote up this proof in full detail.) But the argument did not give a practical algorithm. So, the challenge is just getting a practical way to compute it.
The most interesting thing about the Lebesgue universal covering problem, in my opinion, is that it’s an example of a type of geometry problem that’s easy to state but hard to solve, because we currently have no sophisticated tools for solving it.
Setting a good lower bound is certainly much harder for this problem. One way to proceed is to make some assumption. For example, assume that the best cover is contained in a regular hexagon of unit width. Then any curve of constant width (or orbiform) can only fit in finitely many ways, so the problem becomes more tractable. If you can solve that, then you only have to prove the assumption to finish the job. Try proving that the best cover can be contained within a strip of unit width, then in a parallelogram, … Both parts of this approach are still too hard. Something more is needed.
For the laymen in the audience, what’s the motivation, i.e., what’s the canonical example of a set of diameter 1 that is not covered by a circle of diameter 1?
I don't know what's canonical, but the first example that I thought of is an equilateral triangle whose sides all have length 1.
Oops, I thought of that but confused the circle’s diameter with its radius.
Right, the equilateral triangle is the most obvious set of diameter 1 that doesn’t fit in the circle of diameter 1. From Part 1:
Part 1 then goes on to describe the effect of also considering a regular pentagon, which is the next really important shape.
Read the earlier articles in this series: Part 1, Part 2.
Thanks for bringing this back to life. It is worth adding links to the two posts where we discussed this on n-cat cafe.
https://golem.ph.utexas.edu/category/2015/02/lebesgues_universal_covering_p.html
https://golem.ph.utexas.edu/category/2015/02/computability_for_lebesgues_un.html
Warming to this theme there is the classical Kakeya needle problem. A plane set K is called a Kakeya set if a unit segment, usually referred to as the needle, can be continuously turned around in K so as to return to its original position with its ends reversed. The problem posed by Kakeya was to find a Kakeya set of minimum area. He apparently thought that the answer was the deltoid (three-cusped hypocycloid) with area
. Besicovitch surprised everybody by showing that actually there exist Kakeya sets of arbitrarily small area. In fact it can be proved that given 
, there exists a simply connected Kakeya set of area less than 
contained in a circle of radius 1. F Cunningham, The American Mathematical Monthly, Vol. 78, No. 2 (Feb., 1971), pp. 114-129 contains the details. There is a good exposition in Steven Krantz’s “A Panorama of Harmonic Analysis” (pages 148-170) where he discusses the method of “sprouting” which looks a lot like what is going on with this problem in terms of technique. Just adding this in for those who may not be aware of it and who want to find out more about it.
Yes, you are right to put this in the same class of problem. See this nice Greg Egan animation from G+ https://plus.google.com/113086553300459368002/posts/Ab1LKAxpdDC
As usual Greg Egan has been here before! Very nice.
Since G+ is scheduled to disappear in 10 months, I’ll copy Greg’s post here:
What is the answer if you ask the same question for an equilateral triangle instead of a needle? What is the shape of smallest area which allows an equilateral triangle of unit side to be turned round inside it?
You might think that rotating the triangle in a circle is best but this hypotrochoid is better. Is it the best?
This is nothing against your post, Philip (and congratulations on all your recent success), but I so wish for the day in which the motion of a moving image could be frozen by clicking on the image, and reactivated by clicking again. Sometimes I just want to stare and think without the distracting motion, until I’m ready for it again.
Todd, I agree. I also find this frustrating. Sometimes I download and convert to mp4 using ezgif.com. Here is a youtube version that can be paused
It may still be hard to see but the three vertices trace out the hypotrochoid. The centre of the triangle moves in a circle. The edges of the triangle appear to touch the curve tangentially but actually they only do so at the midpoint.
The curve is defined in the complex plane parametrically up to scale as
for real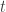 
If you rotate the triangle with unit side about its centre it fits inside a circle of area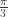
but it can also rotate inside a square of unit area which is smaller. In fact the corners of the square can be cut off by an elliptic arc to give probably the smallest convex solution. If this could be proven it would solve the translation-only version of the Lebesgue covering problem.
The area of this hypotrochoid is
I think.
I don’t think this is the best possible non-convex solution. This problem is closely related to the sofa moving problem and the best solution might also be composed of a number of curve sections joined together so that the edges of the triangle touch the curve more.
It seems that in the first article, you’re searching for a convex subset of the plane that covers any shape of diameter 1 if you allow reflections, but here you seem to allow only translations and rotations. Why did you change the goal this way? Is there a reason to think that the two problems are the same or are not the same?
I think you got it backwards: I didn’t mention reflections in Part 1, but this article here says:
But you raise a very important point! I believe the two problems are not the same: if you allow yourself to reflect your sets of diameter 1, you can fit them in a convex set with smaller area. In the paper Gibbs wrote with Bagdasaryan and me, we really needed to allow reflections to obtain the shape we did. I believe Gibbs’ new paper also uses reflections.
I have tried to edit all 3 articles so they only mention the version that allows reflections, since that’s what we really consider. But both problems are interesting.
It’s also interesting to consider the version that doesn’t demand convexity. I discussed this alternative in Part 1.
It’s also interesting to look at the case where only translations are allowed.
I’d be interested to know what’s currently known about the following problem in a similar spirit, to which Hallard Croft once gave the title The Minimal Living Quarters for a Unit Worm. The problem is to find the shape of least area that contains a translated/reflected/rotated copy of any rectifiable curve of length 1. (The idea is that the worm can sleep in any position it wants to.)
Now that I think about it, I can’t remember whether further conditions are imposed such as convexity. Without such a condition, it isn’t obvious to me whether there could be a measure-zero set that does the job — a sort of Kakeya set for curves rather than segments. It looks pretty unlikely, but off the top of my head I don’t see a proof that it can’t be done.
Philip Gibbs is interested in this problem too, which is known as Moser’s worm problem. Click the Wikipedia link for some more information. There’s both a version that requires convexity and one that doesn’t. So far people have found an upper bound of 0.2709 in the case where we do and 0.270911861 in the case where we don’t. Wikipedia cites a lower bound of 0.232239 in the case where we do require convexity… but not one in the case where we don’t!
For the non-convex case there is a paper by Ward which constructs a set of measure zero that can cover any unit length curve made from a finite number of straight line segments. For general rectifiable curves I don’t think any non-zero lower bound is known. Most work is done on the convex case.
The problem is actually related to Bellman’s lost in a forest problem which is another older unsolved problem. You are lost in a forest with a map showing its shape and size but not where you are or which direction you are facing. For a given forest shape what is the shortest path to follow that guarantees your escape? Proving that a shape is a cover for all curves of unit length is equivalent to proving you have a solution to Bellman’s problem for that shape of forest.
Bellman’s lost in a forest problem reminds me of one i’m sort of working at an elementary and conceptual level (though i have some crazy or speculative ideas so it is related to Ramajan-Hardy type theorems about prime number distribution, partitions of integers, and godel numbering.
. It could be called the ‘lost while climbing the highest mountain problem’.
You are climbing the highest mountain in a mountain range with many peaks—you want the highest one. .
You are on a trail and come to a place where there are many forks in the trail (or many paths).
You don’t have a good map —just a vague outline of the mountain range—but you do have good intuition or experience about trails. Also you have intuition or can guess which is the highest mountain by just looking at the mountain range.
Which trail do you take?
You want a trail which leads to the highest mountain, and also is the easiest —eg the best route to the top of Mt everest. You dont want to end up in a box canyon , or on a low peak, or take a trail which goes up and down too much.
You also have a ‘time and energy budget’—you can’t spend too much time and energy blundering around the wrong trail and have to turn back to try another. Yu don’t have any food, and its going to get dark soon.
Also since you dont exactly know which is the highest peak , you have to decide when you ‘get to the top’ if you should, be satisfied that you climbed the highest one, name it after yourself and make a monument, and go back. Or instead keep going on to find a higher mountain or turn around and check out another trail.
In math, Ramanujan i read apparently could guess what formulas were correct. Wild animals can often guess what the shortest path is up a mountain—they have an intuitive idea about topography. I wonder if one can develop intuition about distribution of prime numbers,partitions of integers, distribution of what i’ve seen called ‘almost prime numbers’ (ie integers divisible by a small number of primes).
(In my own practical applications of this problem , when i come a fork in a trail i check out all the trails for a little while and then choose which to pursue.Often many lead to the same place so they are equivalent. (Keynes: ‘in the long run we are all dead’.
There are other applications of this problem in economics and ecology—and they are likely basically the same problem as studying optimization in a spin glasss with many optima, or a fitness landscape in biology. .)
The Bellman forest problem is now among my favroite problems, which include the ‘information from randomness’ problem (quanta magazine july 2015 —- i have my own possible solution to that using a physical model based on playground equipment–i think visually and sort of physically ) and the wine-water paradox of Keynes and von mises from 1930’s. (I get Keyne’s solution fairly easily but not the many other solutions proposed.)
What you are describing sounds like some kind of tree-search optimisation problem. These come up a lot in computer science, e.g. in game theory. There is a lot known and a lot still to know on those things. There is plenty of scope for new methods still.
Geometric optimisation problems like Bellman’s Lost in a Forest problem are different and nobody seems to have any idea yet of how to solve them except in a handful of special cases. Professional mathematicians ignore them because they are “just highschool geometry”
When the world is full of nanobots these kind if problems will be really important and if mathematicians have not solved them first then big corporations will find the solutions and patent them. Richard Bellman was an applied mathematician many years ahead of his time. He didn’t pose these problems just for fun.
Yes–the Bellman problem and the one you solved on vixra —are very different and less intuitive. (I looked at some of the references with ‘pictures’ and videos and they aren’t intuitive to me.)
I’ve seen the ‘Hamilton-Jacobi-Bellman equation’ in some papers on ecological systems (e.g. applications to fisheries management). It looks to me like a modified diffusion or Fokker–Planck equation—with additional terms, and more complex than standard stochastic processes I’ve seen.
I have seen many algorithms which look applicable to my problem –multiobjective optimization, tree-search. Also concepts like ‘stopping time ‘ and ‘hitting time’ for random walks.
Thanks for response—I’m just interested in this stuff (and also whether there is any ‘back of the envelope approximation’ rather than a very exact technical solution).
Its interesting that Philip Gibbs of (arxiv)^-1 = vixra is on here.
i was reading papers in economic developement on whether ‘deworming campaigns’ conducted by World Bank and Gates foundation were effective. (that’s a health issue). I try to think whether the math and the health go together.
Is that within a convex economic budget of $1?
Here’s a nice popular article on this topic:
• Kevin Hartnett, Amateur mathematician finds smallest universal cover, Quanta, 15 November 2018.
I don’t think I said anything about a “drowning insect”. I find the “skiing across the Antarctic” metaphor a more appropriate expression of the quixotic yet heroic nature of this quest.
Can you provide a human-readable explanation why other shapes of diameter 1 (squares, rectangles, Reuleaux triangles, heptagons, etc) are covered by this shape ?
What do you mean by “this shape”? If you mean the universal covering just discovered by Philip Gibbs, the human-readable explanation is here:
• Philip Gibbs, An upper bound for Lebesgue’s universal covering problem, 22 January 2018.
By the way, your phrase “other shapes of diameter 1” makes me nervous, because while a universal covering covers all shapes of diameter 1, its own diameter is necessarily larger.
Sorry for sounding unclear. I was looking for a simple explanation that Pàl’s original hexagon contains all shapes of diameter 1.
Andreas, here is an outline of the proof.
Firstly you recognise that it is only necessary to consider shapes of constant width one (orbiforms) because all shapes of diameter one fit inside some orbiform.
Secondly you move that orbiform so that it fits between two opposite edges of the hexagon which are distance one apart. Keeping it between those two edges you slide it along until it fits between another pair of edges. It now just fails to fit between the third pair of edges by some offset distance
Now rotate the orbiform through an angle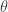
keeping it between the first two pairs of edges. For each angle there is an offset distance 
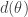by which it fails to fit between the third pair of edges. If it can be shown that 
for some angle 
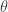then the proof is complete.
The next step is to show that
. If you draw it out you should be able to see why that is. So the offset is either zero for all angles or it is positive for some angles and negative for other angles. It is a continuous function of the angle so the conclusion now follows from the intermediate value theorem.
An excellent distillation of the proof.
It looks like all the work in this area is talking about a “representative” subset S of all diameter 1 shapes, such that anything that covers all shapes in S covers all diameter 1 shapes. How small can you make S? Can it be made finite?
That’s a great question; I don’t know the answer, but making it finite, if that were possible, would be a big step toward solving the problem.
All work on lower bounds for the area involves a specific finite subset of diameter 1 shapes that is probably not actually sufficient. Gibbs’ new upper bounds involve the set of all ‘orbiforms’, which is sufficient but infinite.
It is a great question and we are a long way from answering it.
When the boundary of the shape was composed of straight lines and arcs it did look like some finite set might be sufficient. However, the new upper bound has a more complex curve as part of its boundary. It requires a one-parameter family of shapes to define it.
That’s not conclusive but it is persuasive evidence that a finite set won’t be sufficient.
this is irrelevant but i looked up ‘orbiform’—its on wikipedia. good idea. this remjinds me of whether the membership in ‘mandelbrot set’ is decidable—i gather it isn’t. smale-blum… the pop article says gibbs is an ‘amateur’—a PhD in physics Kan’t count? (i once saw a lecture by John wheelr when he was like 90 years old—he said a boundary of a boundary is zero. thats was among the top lectures i saw—h simon (economics), M Freedman (topology) , were also in that class. i basically didnt understand much.
The literal meaning of amateur mathematician in English is someone who is not a professional, i.e. someone who does maths as a pastime rather than a paid job. The first line of the quanta article makes it clear that this is the intended meaning. The word amateur also has the unfortunate secondary meanings of unskilled or unqualified. I prefer to describe myself as an independent mathematician/physicist to avoid that ambiguity.
Hi Philip:
I have seen your code that is available on Github and I create an issue with a little doubt about the code:
Why the value of the local variable C is not used on nearestPoint method?
https://github.com/PhilipGibbs/Lebesgue/blob/d4ad5f9960ca57f55138f184672793f80241d704/Lebesgue.java#L272
Thank you.
Sorry, this is the method:
The var C is never used:
https://github.com/PhilipGibbs/Lebesgue/blob/d4ad5f9960ca57f55138f184672793f80241d704/Lebesgue.java#L272
Thanks for looking at the code. C is not needed to find the minimum so it was wasteful to calculate it but it does not cause an error.
I assume the best possible value is 10/(4/3π√8)=0.844046… The value in brackets is the volume of a sphere with radius √2. Unfortunately without proof.
I don’t knkow any reason that number should appear as the best value in the Lebesgue universal covering problem. If it does, you will become famous for that guess.
[…] John Baez, who wrote some blog posts on this problem, […]