Check out the video of Jonathan Lorand’s talk, the second in the Applied Category Theory Seminar here at UCR. It was nicely edited by Paola Fernandez and uploaded by Joe Moeller.
Abstract. In this talk we will look at various examples of classification problems in symplectic linear algebra: conjugacy classes in the symplectic group and its Lie algebra, linear lagrangian relations up to conjugation, tuples of (co)isotropic subspaces. I will explain how many such problems can be encoded using the theory of symplectic poset representations, and will discuss some general results of this theory. Finally, I will recast this discussion from a broader category-theoretic perspective.
Check out the video of his talk above, and also his talk slides. It was nicely edited by Paola Fernandez and uploaded by Joe Moeller.
Here are some papers to read for more detail:
• Jonathan Lorand, Classifying linear canonical relations.
• Jonathan Lorand and Alan Weinstein, Decomposition of (co)isotropic relations.
Lorand is working on a paper with Weinstein and Christian Herrman that delves deeper into these topics. I first met him at the ACT2018 school in Leiden, where we worked along with Blake Pollard, Fabrizio Genovese (shown below) and Maru Sarazola on biochemical coupling through emergent conservation laws. Right now he’s visiting UCR and working with me to dig deeper into these questions using symplectic geometry! This is a very tantalizing project that keeps on not quite working…
Azimuth 
Hi John,
Do you feel like any of this research (chemical reaction networks generally) might benefit from computations/analysis/simulations over very large graphs?
The talk here has nothing to do with chemical reaction networks. But anyway: there are people who do calculations with fairly large graphs in chemical reaction network theory. Here are a few papers I know:
• Jakob L. Andersen, Christoph Flamm, Daniel Merkle, and Peter F. Stadler, Generic strategies for chemical space exploration.
• Jakob L. Andersen, Christoph Flamm, Daniel Merkle, Peter F. Stadler, A software package for chemically inspired graph transformation.
• Omar A. Khalil, Farshad Harirchi, Doohyun Kim, Sijia Liu, Paolo Elvati, Angela Violi and Alfred O. Hero, Model reduction in chemical reaction networks: a data-driven sparse-learning approach.
Sorry, didn’t mean to post off-topic :) I was reading this paper which mentions fixed points, and also looking at the ‘biochemical coupling through emergent conservation laws’ paper, and just trying to figure out where everything fit in. I’ve been starting to work on some large-scale distributed graph code, so I was just wondering what was being done in this area. Thanks for the links! They give me a good sense of what is being done.
This is kind of a stretch, but who else to ask?
The objects in the ever-astounding field of “symplectic resolutions” are complex symplectic (not Kähler — the 2-form is (2,0) not (1,1)) manifolds whose affinization map
is birational. As you know, the morphisms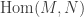 
are the Lagrangians in 
.
However, it appears to me that this isn’t quite the right category — the manifolds should come equipped with a symplectic circle action with compact fixed-point set. It’s then very interesting (Maulik-Okounkov’s approach to R-matrices) to consider changing the circle action on a given symplectic resolution.
Have you run into this wrinkle? In particular, do you know what the morphisms in this richer category should be?
Well their data is used to build targets for topological strings (as per later Okounkov w/ Mina etc), so what sort of changing the targets from X to Y do we need that we want to be in Hom(X,Y). Just a start for the ever daunting physical theorem to mathematical definition process.