I’m almost done explaining why any presheaf category is an elementary topos, meaning that
• it has finite colimits;
• it has finite limits;
• it’s cartesian closed.
• it has a subboject classifier.
Last time I explained why such categories are cartesian closed; now let’s talk about the subobject classifier!
Subobject classifiers
In the category of sets, 0-element and 1-element sets play special roles. The 0-element set is the initial object, and any 1-element set is a terminal object. But 2-element sets are also special! They let us talk about ‘truth values’.
We can take any such set, call it 2, and call its elements ‘true’ and ‘false’. Then subsets of any set correspond in a one-to-one way with functions
by associating to any subset the function taking the value ‘true’ on
and ‘false’ elsewhere: its characteristic function.
The idea of a subobject classifier is simply to copy this idea in other categories. A subobject classifier, which we’ll call will serve as an ‘object of truth values’ in the category at hand. To make this precise, we’ll demand that subobjects of any object
correspond bijectively to morphisms
That’s the idea. But to make the idea useful we need to say how subobjects of correspond to morphisms
And of course before that we’ll need to say exactly what a subobject is!
In we can pick out a subset of
using a monomorphism
where I use the funny arrow to denote a monomorphism (affectionately known as a ‘mono’). The idea is that the image of
is the subset of
we care about. But two different monos can have the same image, so we have to be careful!
Suppose we have two different monos
and
in When do they have the same image? The answer is: precisely when there’s an isomorphism
such that
Puzzle. Prove this.
So, more generally, in any category, we shall say that two monos and
are isomorphic iff there’s an isomorphism
such that
Definition. A subobject of an object in a category
is an isomorphism class of monos into
We will eventually study subobjects to see how much they behave like subsets—there’s a lot to say about that! But first let’s see what a subobject classifier is.
Again we return to the category to see how this should work. We need to know how subobjects of
arise from functions
For this we need to know which elements of
get mapped by
to ‘true’, so we need to specify which element of the set
counts as ‘true’. We do this using a function
which of course is a mono. Then, given any function
we can take the pullback of along
and get a mono
Please see diagram (2) in Section I.3 of Mac Lane and Moerdijk to see this pullback in all its glory.
The usual description of pullbacks in assures us that
and the map is the obvious inclusion.
We can copy this procedure in any category with pullbacks, leading to the definition we seek:
Definition. Let be a category with pullbacks. A subobject classifier is an object
equipped with a mono
such that for any object there is a bijection between morphisms
and subobjects of given as follows: for any such morphism
, we pull back
along
obtaining a mono
and then take the subobject of corresponding to this.
Here we are using a fact:
Puzzle. Show that the pullback of any mono is a mono.
Thus, is automatically a mono, because we are assuming
is.
Subobjects in presheaf categories
Let’s see what subobjects and subobject classifiers look like in presheaf categories. So now let be any category and let
be the category of presheaves on
To get started: what are monos in like? Remember from Part 5 pullbacks are computed pointwise in presheaf categories. Furthermore, monos can be defined in terms of pullbacks:
Puzzle. Show that a morphism is a mono iff its pullback along itself is the identity
This implies that determining whether a morphism in is a mono must also be a ‘pointwise’ matter: that is, one that you can check by looking at one object
at a time. But you can prove this directly:
Puzzle. Let be a morphism between presheaves
that is, a natural transformation between functors
Show that
is a mono iff for each
is a mono in that is, a one-to-one function.
Thus, people say a morphism of presheaves makes
into a subpresheaf of
when each function
is one-to-one, so
corresponds to a subset of
It’s good to look at this in examples, like the case of graphs, where we get the concept of ‘subgraph’: one graph included in another.
Of course, we should remember that a subobject of really an equivalence class of monos. Two different monos
and
give the same subobject of
if there’s an isomorphism between
and
that makes the obvious triangle commute. But sometimes people slack off and say
is a subobject of
if it’s equipped with a mono
I was coming close to doing that in the last paragraph.
Subobject classifiers in presheaf categories
Now we’re ready to understand the subobject classifier in a presheaf category. I’ll just tell you what it is. The subobject classifier in the presheaf category assigns to each object
the set of ‘sieves’ on
So what’s a sieve?
Definition. Given a category , a sieve on an object
is a collection of morphisms to
such that if
is in the sieve and
is any morphism, then
is in the sieve.
In other words, a sieve is a collection of morphisms with a fixed target that’s closed under precomposition. The name ‘sieve’ should remind you that if a piece of grain can get through a sieve, any smaller piece of grain can also get through. You can think of as ‘smaller’ than
in some sense.
Here’s a slick way to think about sieves. Remember that the Yoneda embedding
sends any object to a presheaf
called a representable presheaf.
Here’s the cool fact: a sieve on is just the same as a subobject of
For each object
it gives a subset of
and for each morphism
it gives a map from
to
namely the map sending each
to
The subobject classifier in
is a beautiful thing: it assigns to each object the set of all sieves on that object!
That is, for each object the set
is the set of all sieves on
But we also need to say what
does to morphisms. Given a morphism
the map
sends sieves on to sieves on
as follows. For any sieve
on
we say a morphism is in
if its composite with
is in
We also need to describe
A terminal presheaf sends each object of
to a one-element set, so
must pick out an element of
for each object
in a natural way (it’s a natural transformation.)
In other words, must choose a sieve on
for each
in a natural way. The naturality condition here says that if
a morphism is in the chosen sieve on
iff its composite with
is in the chosen sieve on
How does do this wonderful thing? Simple: for each object
it chooses the sieve containing all morphisms to
Then the naturality condition holds trivially.
Of course, we have to check that
really is a subobject classifier for Only this will let us really understand what we’ve done here.
I’ll talk about this more next time, perhaps focusing on examples to build up intuition. For now I recommend that you read Section I.4 of Mac Lane and Moerdijk’s book for a general proof—and also a look at some examples!
The series so far:
• Part 1: sheaves, elementary topoi, Grothendieck topoi and geometric morphisms.
• Part 2: turning presheaves into bundles and vice versa; turning sheaves into etale spaces and vice versa.
• Part 3: sheafification; the adjunction between presheaves and bundles.
• Part 4: direct and inverse images of sheaves.
• Part 5: why presheaf categories are elementary topoi: colimits and limits in presheaf categories.
• Part 6: why presheaf categories are elementary topoi: cartesian closed categories and why presheaf categories are cartesian closed.
• Part 7: why presheaf categories are elementary topoi: subobjects and subobject classifiers, and why presheaf categories have a subobject classifier.
• Part 8: an example: the topos of time-dependent sets, and its subobject classifier.


Typos: should be
should be 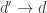 , and $\Omega(f)(S)$ should be
, and $\Omega(f)(S)$ should be 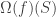 .
.
Thanks — fixed!
Let’s look at an example of a presheaf topos, to see what various things I’ve been talking about actually look like—especially the subobject classifier.