Merry Xmas, Ymas, and Zmas—and a variable New Year!
For a long time I’ve been meaning to update this list of open questions on the Physics FAQ:
• Open questions in physics, Physics FAQ.
Here’s what it said about neutrinos as of 2012:
• What is the correct theory of neutrinos? Why are they almost but not quite massless? Do all three known neutrinos—electron, muon, and tau—all have a mass? Could any neutrinos be Majorana spinors? Is there a fourth kind of neutrino, such as a “sterile” neutrino?
Starting in the 1990s, our understanding of neutrinos has dramatically improved, and the puzzle of why we see about 1/3 as many electron neutrinos coming from the sun as naively expected has pretty much been answered: the different neutrinos can turn into each other via a process called “oscillation”. But, there are still lots of loose ends.
It’s held up fairly well: all of those questions are still things people wonder about. But I should add a question like this, because it’s nice and concrete, and physicists are fascinated by it:
• Is the tau neutrino heavier than the mu and electron neutrinos, or lighter?
This is a bit sloppy because the neutrinos of definite mass are linear combinations of the neutrinos of definite flavor (the electron, mu and tau neutrinos). The neutrinos of definite mass are called mass eigenstates and the neutrinos of definite flavor are called flavor eigenstates. This picture by Xavier Sarazin makes the two competing scenarios clearer:
In the normal hierarchy the mass eigenstate that’s mainly made of tau neutrino is the heaviest. In the inverted hierarchy it’s the lightest.
We don’t know which of these scenarios is correct. The problem is that we can’t easily measure neutrino masses! The rate at which neutrinos oscillate from flavor to flavor gives us information about absolute values of differences of squared masses! Currently we’re pretty sure the three masses obey
and
So, 
We also don’t know which is bigger, 
By the way, I will bet that we’ve got the normal hierarchy, with 
I also want to change this question to something less technical, so people realize what a big deal it is:
Could any neutrinos be Majorana spinors?
A less technical formulation would be:
• Is any kind of neutrino its own antiparticle?
On the one hand it’s amazing that we don’t know if neutrinos are their own antiparticles! But on the other hand, it’s really hard to tell if a particle is its own antiparticle if its very hard to detect and when you make them they’re almost always whizzing along near the speed of light.
We’d know at least some neutrinos are their own antiparticles if we saw neutrinoless double beta decay. That’s a not-yet-seen form of radioactive decay where two neutrons turn into two protons and two electrons without emitting two antineutrinos, basically because the antineutrinos annihilate each other:
Physicists have looked for neutrinoless double beta decay. If it happens, it’s quite rare.
Why in the world should we suspect that neutrinos are their own antiparticles? The main reason is that this would provide another mechanism for them to have a mass—a so-called ‘Majorana mass’, as opposed to the more conventional ‘Dirac mass’ that explains the mass of the electron (for example) in the Standard Model.
I will bet against the observed neutrinos being their own antiparticles, because this would violate conservation of lepton number and an even more sacred conservation law: conservation of baryon number minus lepton number. On the other hand, if some so-far-unobserved right-handed neutrinos are very heavy and have a Majorana mass, we could explain the very light masses of the observed neutrinos using a trick called the seesaw mechanism. And by the way: even the more conventional ‘Dirac mass’ requires that the observed left-handed neutrinos have right-handed partners, which have so far not been seen! So here’s another interesting open question:
• Are there right-handed neutrinos: that is, neutrinos that spin counterclockwise along their direction of motion when moving at high speeds?
So many unanswered questions about neutrinos!
My list of references hasn’t held up as well:
For details, try:
• The Neutrino Oscillation Industry.
• John Baez, Neutrinos and the nysterious Maki-Nakagawa-Sakata Matrix.
• Paul Langacker, Implications of neutrino mass.
• Boris Kayser, Neutrino mass: where do we stand, and where are we going?.
The first of these has lots of links to the web pages of research groups doing experiments on neutrinos. It’s indeed a big industry!
In fact the first page is now full of silly random posts, but oddly still titled NeutrinoOscillation.org. Paul Langacker’s page is missing. Boris Kayser’s review uses an old link to the arXiv, back when it was at xxx.lanl.gov. His review is still on the arXiv, and it’s nice—but it dates to 1998, so I should find something newer!
What are the best places to read a lot of clearly explained information about neutrino puzzles? Are there other big neutrino puzzles I should include?
Azimuth 
Isn’t conservation of B-L something that we expect to be violated in quantum gravity? There was a recent paper by Daniel Harlow and Hirosi Ooguri in which they argued that there are no global symmetries (like B-L) in AdS/CFT. Granted, we don’t live in an AdS universe, but they mention that people (like Wheeler) have conjectured this to be true in quantum gravity in general.
Anything anyone says about quantum gravity should be taken with a big grain of salt! Yes, a bunch of people expect that B-L is not conserved by quantum gravity. For example: a proton could fall into a black hole, and later it could emit a positron, and charge would be conserved but not baryon number minus lepton number.
But all this seems quite different to me than ordinary quantum field theory; if neutrinos have a Majorana mass and they annihilate each other due to that, then B-L would be violated for straightforward quantum field theory reasons that have nothing to do with quantum gravity. I don’t see any fundamental reason why that can’t happen, I just don’t want to go throwing away conservation laws until experiments or damned good theoretical arguments force me to.
In the Standard Model, baryon and lepton number are—in theory—-separately not conserved, due to sphalerons, which convert three baryons to three antileptons. Nobody has actually seen this happen. B-L is still conserved by sphalerons.
By the way, here’s a nice summary of how B-L works in the two most famous grand unified theories:
• Cosmas Zachas, B-L global symmetry in the grand unification theories, Physics StackExchange.
“Anything anyone says about quantum gravity should be taken with a big grain of salt!”
Such a grain should definitely be bigger than 0.00002 grams. :-)
I’m reading old papers on grand unified theories. Way back in 1981, in the The Second Workshop on Grand Unification, Sheldon Glashow wrote:
I think it’s cool how the usual 15-dimensional representation of the Standard Model gauge group G admits exactly one extra current that’s free of gauge-gauge-current anomalies. I should translate that into stuff about Lie algebra representations (which would have been trivial for Glashow).
You wished us a merry Zmas, but it’s W mass that actually appears in this post!
Ho ho ho!
Under which conditions, the coherence of the neutrino mass eigenstates is lost?
I’m not sure what that even means. Are you asking when a neutrino in a mass eigenstate gets quantum entangled with its environment—aka decoherence?
As a clueless mathematician, I don’t understand the notion of “flavor eigenstates”. Eigenstates of which operator? This issue arises with quarks as well as with leptons; so I’ll describe it for quarks, where the continuing uncertainty about neutrinos plays no role. Maybe you can eliminate my confusion.
Here is the Lagrangian picture I am coming from (before symmetry breaking). There are six types of fermions: the (right-handed) up-quark, (right-handed) down-quark, (left-handed) quark, (right-handed) electron, [presumably] (right-handed) neutrino, and (left-handed) lepton types. Let’s use the letters
to distinguish them. To each type 
corresponds a representation 
of the Lie group 
on a complex vector space 
, where 
(or 
if you prefer). In addition there is a 3-dimensional complex vector space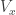 
that describes the three particle generations. We have an 
-principal bundle 
over spacetime. The fermion fields correspond to sections in the complex vector bundles 
, where 
and 
, and where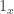 
is the trivial representation on 
.
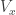The terms in the Standard Model Lagrangian which involve fermions are the Yukawa terms (describing interactions of one Higgs and two fermions) and the terms describing interactions of two fermions (of the same type) and one gauge boson. The latter terms involve only a scalar product on each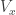
; no operator occurs whose eigenstates could yield a decomposition of 
.
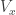The Yukawa terms involve linear maps
and 
and 
, and [presumably] 
. We can consider the eigenvalues of 
and 
. These are the quark-mass eigenvalues. In the physical and generic case of three distinct eigenvalues, we obtain decompositions of 
and 
into one-dimensional “mass eigenstates”. (Correspondingly, we get two different decompositions of 
into one-dimensional subspaces. “The” CKM matrix is a basis change from an orthonormal eigenvector basis of 
to one of 
.)
As far as I can see, these are all generation-space decompositions that arise from the parameters which occur in (the renormalizable part of) the Standard Model Lagrangian. So, what is a “flavor eigenstate”?
The flavor operator, of course. This is an operator on the 3-dimensional complex vector space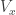
that describes the three particle generations. It has 3 distinct eigenvalues, whose actual values don’t really matter: let’s assume they are 1, 2, and 3. What matters are the eigenvectors. For neutrinos, the eigenvectors with eigenvalues 1, 2, and 3 are called electron neutrino, mu neutrino and tau neutrino, respectively.
(As usual, these eigenvectors are only well-defined up to a phase: that is, you’re free to multiply an eigenvector by any unit complex number and get another eigenvector.)
How do we specify these eigenvectors (up to phase)? That is, what makes them special?
Let me start by doing it operationally, as if I were an experimentalist. I’m sure you will find this infuriating, but we are doing physics here, so you have to get used to it. We can then attempt to translate this into math.
When an antineutron decays, it usually turns into an antiproton, a positron and a neutrino. One can ask which state the neutrino is in when it’s first formed by this process. And I’m not talking about its momentum or spin here, just its ‘flavor’, which is described by a vector in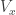
.
The answer is: when it’s first produced by this process, it’s an electron neutrino. This is an operational definition for a particular unit vector in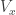
, one of the three flavor eigenstates. (Again, it actually defines this vector only up to a phase.)
We can describe similar experiments that produce mu neutrinos and tau neutrinos.
But back to our electron neutrino! This state is not one of the eigenstates of the mass operator you described. So, as the neutrino shoots away, it will ‘oscillate’. That is, if we write its state as a time-dependent vector
, the magnitude of its components in the electron neutrino, mu neutrino, tau neutrino basis will change with time. You can detect this by trying to do a reverse reaction: e.g., trying to get your neutrino to hit an antiproton and turn it into an antineutron and a positron. This particular reverse reaction is a way to measure
Okay, so that was one attempt to explain flavor eigenstates. I doubt it will satisfy you, given how you set up your question. Here’s another.
If you already know and love mass eigenstates, it’s sufficient to give a unitary 3 × 3 matrix that maps mass eigenstates to flavor eigenstates. This matrix is here. It’s called the Pontecorvo–Maki–Nakagawa–Sakata matrix. It’s the neutrino analogue of your friend the CKM matrix, so anything you know about the CKM matrix applies here too. The linked source says:
Note that both the mass eigenstates and flavor eigenstates are only defined up to phase, so the components of this 3 × 3 matrix
are not physically measurable things: what really ‘exists’ is the orbit of 
under transformations of the form
where
are diagonal unitary matrices.
I think this will let you start translating what I’m saying into your framework, which may be designed to avoid the ‘ambiguity’ introduced by the matrices
and 
. If you succeed in doing the translation, please explain it to me!
I got confused with your description because you started with a 3-dimensional vector space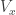
and then introduced three separate vector spaces, e.g. 
and 
and 
which might or might not have canonical isomorphisms between them. Following traditional physics I am working with a single 3-dimensional vector space 
Perhaps I’m paying a price for this with matrices
and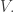 
But these express the usual ambiguities one runs into when trying to choose ‘the’ orthonormal basis of eigenvectors of a self-adjoint operator with distinct eigenvalues. In reality we don’t have an orthonormal basis here, what we have is a direct sum decomposition of a three-dimensional Hilbert space into 3 orthogonal one-dimensional subspaces.
If you are, as you claim, a mathematician, you either learned the Standard Model from some fancy book on “the Standard Model for mathematicians” written by a mathematician who wanted to present it differently from usual, or you learned it from ordinary textbooks, figured out a more invariant way to describe everything, and then expunged terms like “flavor eigenstate” from your memory. Or maybe you decided that “flavor eigenstate” was meaningless and you’re trying to test me to see if I can justify the concept!
I’m curious which one is the case—and what that book on “the Standard Model for mathematicians” was, if that’s where you picked up your way of talking about things.
Do these experiments still involve a proton and a neutron, just with a muon instead of an electron? Or do they also require a strange and charm quark to get exactly the right state? (I'm suppressing the ‹anti›s here.)
The only thing the down quark in the decaying neutron does for you is produce a virtual W– boson that then becomes an electron and an electron neutrino:
A W– can also turn into a muon and a muon antineutrino, or a tau and a tau antineutrino. However, the energy in the W– produced in neutron decay is too low to create muon or tau antineutrinos this way. The mass of a muon exceeds the mass of a neutron minus the mass of a proton. And a tau is even worse.
A ‘systematic’ but not practical way to create and distinguish between electron, muon and tau antineutrinos would be this: create an actual, non-virtual W– boson. It can decay in various ways, but three basic ones are:
• an electron and an electron antineutrino
• an muon and a muon antineutrino
• a tau and a tau antineutrino
So if you see a muon coming out you know you’ve produced a muon antineutrino, and so on for the three cases.
If you want a muon antineutrino, a much more practical thing to do is this. Create a muon by whatever means, then let it decay:
You’ll have produced an electron antineutrino and a muon neutrino. Now, if you can tell neutrinos from antineutrinos, you’re good to go.
Nobody said this stuff had to be easy. If you try to explain to me how to get ahold of ytterbium (and make sure it’s not yttrium or some other rare earth), it’s bound to be complicated.
Apologies for the delayed reply. It’s still incomplete, and I see that Toby Bartels has by now said some things similar to what I wanted to say. Anyway, here is my take on the issue.
First one remark. You wrote: “Let me start by doing it operationally, as if I were an experimentalist. I’m sure you will find this infuriating […]” Quite the contrary. If someone doesn’t understand a physical concept, operational explanations are ultimately the only ones that can help. But I think we can figure this out without getting too operational.
You said: “If you succeed in doing the translation, please explain it to me!” I’ll try. I hope to avoid the old trap of “mathematicians translating something into their own language and henceforth it’s something completely different”.
PART 1.
Let
. In the Standard Model (SM), fermionic fields of type 
correspond to sections in a certain complex vector bundle 
over spacetime, namely the associated vector bundle of some 
-principal bundle via a suitable representation 
of 
on a tensor product 
. Here 
is a representation of 
on a complex vector space 
; and 
is the trivial representation of 
on a 3-dimensional complex vector space 
, which I’ll call the “generation space” of 
. In the following discussion we do not have to care too much about 
and 
. (You know what they are.)
The PMNS matrix for the leptons is analogous to the CKM matrix for the quarks, so let’s consider only the latter. The relevant fermion types are the (right-handed) up-quark field
(in all three generations: up, charm, top), the (right-handed) down-quark field 
(in all three generations: down, strange, bottom), and the (left-handed) quark-field 
(a “doublet” in physics lingo).
The generation spaces
are a priori not equipped with any structure: no scalar product, no decomposition into one-dimensional subspaces, no identifications between them. (You said that the three spaces should be identified. I hope to convince you that they shouldn’t.)
The (renormalizable part of the) SM Lagrangian contains two types of terms involving fermions:
Terms that describe interactions of two fermions (of the same type
) with a gauge boson. Schematically they look like 
, where 
is a certain first-order differential operator constructed from the gauge-boson field 
(a “twisted Dirac operator” in mathematical lingo). More about the bilinear form 
below.
and either 
or 
) and one Higgs boson.
Yukawa terms that describe interactions of two fermions (in our quark case:
(to be continued…)
One thing that I've learnt over the course of the past few days (and discussed somewhat in the comments to Part 2 of these neutrino posts) is that flavour is defined differently for neutrinos than it is for quarks. For quarks and charged leptons, flavour states are mass states; for neutrinos, they're not. There are practical and historical reasons for this difference, but it is ultimately an arbitrary choice. So when you translate this discussion about quarks into a discussion about leptons, you turn u,c,b into e,μ,τ but d,s,t into ν₁,ν₂,ν₃. The PMNS matrix expresses νₑ etc as linear combinations of ν₁,ν₂,ν₃; analogously, the CMK matrix expresses d′,s′,t′ as linear combinations of d,s,t.
So the real distinction is not between mass states and flavour states but between mass states and weak states. For neutrinos, the flavour states are defined to be the weak states; for everything else, they're defined to be the mass states. The mass states, of course, are eigenstates of mass; the weak states are eigenstates of mass-after-emitting-or-absorbing-a-W-boson. That is, an interaction mediated by a W boson turns a mass state into a weak state or vice versa. It turns flavour states into flavour states if you’re talking about leptons, but not if you’re talking about quarks; this is only because the conventions are different, not the underlying mathematics and physics.
[In PART 1, the numbering of my two-item ordered HTML list got lost in the translation.]
PART 2.
Let’s start with the first type of fermion-involving Lagrangian. (Is there a standard name for these terms, analogous to “Yukawa terms”?)
The (real-valued) bilinear form
is determined by a sesquilinear form 
, as follows: 
is a section in the associated bundle 
constructed from the representation 
on $S_\psi\otimes V_\psi$, and 
is a section in another associated bundle constructed from a representation 
of 
on some tensor product 
. There is a nonzero sesquilinear form 
which is invariant under simultaneous application of 
on the left-hand resp.\ right-hand side. This sesquilinear form is unique up to multiplication with a complex number. We may pick any such form without loss of generality. From 
and 
we get in the obvious way a sesquilinear form 
whose real part gives us the bilinear form 
.
Without loss of generality we may assume that
is hermitian: The antihermitian part yields a Lagrangian term that vanishes due to a partial integration argument (as long as we consider for instance compactly supported fields).
We can regard the hermitian forms
as parameters of the SM Lagrangian. But, as an experimental fact, each of them is positive definite, i.e. a scalar product, for the universe we live in. (What does a universe look like where they have other signatures?)
Since all scalar products are isomorphic, they produce the same physics. In this sense, there is no need to include
in the list of SM parameters. (Alternatively, we can include their isomorphism classes [i.e. their signatures] as a finite-valued parameter of the SM.)
To summarize PART 2: The a priori structureless generation vector spaces
obtain scalar products from the first type of fermion-involving SM Lagrangians. They still have no decomposition into one-dimensional subspaces at this point, and there are no identifications between them.
(to be continued…)
PART 3.
Now the Yukawa terms.
Let
denote the Higgs field. There are two Yukawa quark terms. One involves 
, the other one involves 
. Only the generation tensor factors are relevant for our discussion. The Higgs field does not have a generation factor, hence can be ignored here.
We just need sesquilinear forms
and 
to write down the Yukawa terms. Since 
is equipped with a (sesquilinear) scalar product 
(this is not the bilinear form from PART 2; clash of notation), we can identify 
with a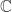 
-linear map 
via 
. Analogously 
corresponds to a 
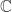-linear map 
.
These two maps
are parameters of the SM Lagrangian and determine the Yukawa quark terms. (I will not describe these terms in detail. They involve invariant trilinear forms on the non-generation tensor factors. Again these trilinear forms are essentially unique.)
(The Yukawa terms are the only renormalizable two-fermions-one-Higgs Lagrangians which we can form from
and which are allowed by general symmetry principles. The two maps 
parametrise all possibilities!)
Now we can figure out which decompositions of the vector spaces
these maps induce.
Via the scalar products we get adjoints
and 
. The obvious decompositions are:
the
-eigenspace decomposition of 
(the corresponding eigenvalues are physically the squares of the down-quark masses);
-eigenspace decomposition of 
(with the same eigenvalues as 
);
-eigenspace decomposition of 
(the corresponding eigenvalues are physically the squares of the up-quark masses);
-eigenspace decomposition of 
(with the same eigenvalues as 
).
the
the
the
(If
were somehow identified, we would get many additional endomorphisms and hence many other decompositions from the Lagrangian parameters 
!)
In the physically relevant (and mathematically generic) case, all eigenvalues are distinct. Hence (in this case) each decomposition is an orthogonal decomposition into three one-dimensional subspaces.
Now we have two orthogonal decompositions of
into one-dimensional subspaces: one decomposition 
induced by 
, the other 
by 
. Let’s say 
is the eigenspace for the eigenvalue 
, where 
; analogously with 
instead of 
.
If we fix in each of these subspaces a vector of norm 1, then we get a matrix
describing the basis change from the 
-basis to the 
-basis. Each such matrix is called a "CKM matrix". There are many such matrices, because there are many ways to fix vectors of norm 1 in the eigenspaces: multiplying each of the six chosen vectors with an element of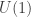 
yields another possible choice. Each CKM matrix arising in this way describes the same physics: only the eigenspace decompositions are physically/operationally meaningful.
(to be continued some day…)
Correction of the sentence with the “Formula does not parse” errors:
We just need sesquilinear forms
and 
to write down the Yukawa terms.
PART 4.
Let’s express the discussion from PART 3 differently.
We have two complex-linear maps
between 3-dimensional unitary spaces; the target space is the same for both maps. We want to classify the possible pairs 
up to three separate unitary basis changes: on each domain and on the common target.
After introducing irrelevant bases everywhere, the task is to determine the orbit space of the following group action of the group
on the set 
: For 
and 
,
$
$
Let
be the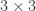 
identity matrix, and let 
. The group action of 
we just considered induces a group action of 
on 
. We want to determine its orbit space.
We expect the dimension of the orbit space to be the (real) dimension of
minus the dimension of 
. That is, 
minus 
. I.e.,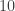 
.
Let’s consider the subset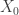
consisting of all 
such that 
and 
each have three distinct positive eigenvalues. This is an open dense subset of 
which is preserved by the action of 
. We expect the orbit space of the action on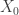 
to be 10-dimensional as well.
Experiments show that the SM parameter
lies in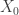 
. Therefore physicists care only about the orbit space of 
.
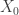The discussion from PART 3 boils down to the message that this orbit space can be parametrized by six numbers (the quark masses), which can be thought of as the noncompact part of the orbit space; and by the compact part, which can be thought of as the set of possible CKM matrices modulo a suitable group action. Namely the following action of the group
on the set 
:
$
$
The expected dimension of the compact part is the dimension of
(i.e. 
) minus the dimension of 
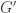(i.e.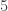 
). Which yields an orbit space of expected dimension 
.
The whole point of this classification is that the three generation spaces are not identified but considered as separate spaces. This discussion can be found in physics textbooks (up to differences in notation and language, of course), for instance O. Nachtmann: Elementary particle physics. Concepts and phenomena, pp. 362–364.
We should continue with a translation of “flavor eigenstates” into the language above…
The symbol
was supposed to be a boldface 1. Moreover, unordered HTML lists do not seem to work properly either. Is there any tool, here or elsewhere, to preview the rendering of a post?
Here’s how someone named Vanadium reacted to the FAQ questions over on Physics Forums… and here are my replies:
• Do all three known neutrinos—electron, muon, and tau—all have a mass?
I meant the three mass eigenstates that most closely line up with the electron, muon, and tau flavor eigenstates. I need some nontechnical way to say what I mean. This is for ordinary folks, so words like “eigenstate” are not allowed. I guess the best way is something like this: “Is there a massless neutrino, or do they all have nonzero mass?”
I’m interested that you think maybe it’s no longer possible to get a theory with one massless neutrino and two massive ones to fit the data. Back when I was paying attention it was theoretically possible.
• Are the two neutrinos with very close masses the light ones, or the heavy ones?
Okay. I haven’t been keeping up with this stuff for the last decade or so. If experts feel pretty convinced that normal ordering is the right scenario, this question shouldn’t be on the list!
• Are there right-handed neutrinos: that is, neutrinos that spin counterclockwise along their direction of motion when moving at high speeds?
I meant chirality, and I meant “in the limit as the speed approaches c”. I don’t know a great way to state this question to nonexperts without using words like “helicity” and “chirality”, which I’d rather avoid.
• Are there sterile neutrinos: that is, neutrinos that don’t interact with other particles via the strong, weak or electromagnetic force?
How does the sterile one mix with the others? Does it only couple to them via the Higgs or some other mass-generating mechanism? If so I think my description was not too bad.
As long as it’s a question lots of physicists are asking, it can be on this list. But actually it could be better to ask a more general question, like “Are there extra neutrinos beyond the three known ones and their three possible right-handed counterparts?”
(I’ll reply to your other comments later. It’s going to be a long reply…)
You wrote: “Are there sterile neutrinos: that is, neutrinos that don’t interact with other particles via the strong, weak or electromagnetic force?”
This sterile neutrino definition is indeed not the one used in the technical literature. The Introduction to the Light Sterile Neutrinos White Paper https://arxiv.org/abs/1204.5379 says: “A sterile neutrino is a neutral lepton with no ordinary weak interactions except those induced by mixing. […] It may participate in Yukawa interactions involving the Higgs boson or in interactions involving new physics.”
Thanks for providing an ‘official’ definition. Mine was pretty close, but I should have said something like this: it doesn’t interact directly with the strong, weak or electromagnetic force. By interacting with the Higgs or new yet-unknown particles it may turn into another kind of neutrino which does interact with the weak force. And of course it interacts with everything via gravity.
I think another good question is a more fine-grained Majorana one: if the neutrinos we see are Majorana, is this due to a seesaw mechanism? If so, type I, II, III, or something more baroque?
I don’t know how you translate that into more approachable language, though :P
I like how https://arxiv.org/abs/1802.05722 presents the seesaw types, it’s more organized/principled than other presentations I’ve seen.
Thanks very much! That paper looks pretty clear, at least for people who know some particle physics. I’ll add it to the list of references in the FAQ. That’s easier than trying to explain all this myself. I do want to keep learning more about this, though.
Everyone knows about solar neutrinos, so some smart aleck was bound to think of this:
• S. Demidov and D. Gorbunov, Lunar neutrinos.
Apparently observed neutrinoless double beta decay would Pin down the signature of spacetime to just the (-+++) signature? https://arxiv.org/abs/math-ph/0012006
Wow, that’s cool! I’d seen DeWitt–Morette talk about how the Pin group works differently for (- + + +) and (+ – – -) signatures, and by now I know this math pretty well… but at the time I wasn’t at all interested in neutrinoless double beta decay, so I didn’t realize this is an actual experiment that could shed light on the signature of spacetime! I’ll have to reread this paper!
Nice pun, too.
By the way, “Vanadium” on Physics Forums convinced me that it’s not worth listing the normal hierarchy / inverted hierarchy question as an open question. Right now people seem to think there’s about a 95% chance that normal hierarchy scenario is correct.