Last time we worked out an analogy between classical mechanics, thermodynamics and probability theory. The latter two look suspiciously similar:
| Classical Mechanics | Thermodynamics | Probability Theory | |
| q | position | extensive variables | probabilities |
| p | momentum | intensive variables | surprisals |
| S | action | entropy | Shannon entropy |
This is no coincidence. After all, in the subject of statistical mechanics we explain classical thermodynamics using probability theory—and entropy is revealed to be Shannon entropy (or its quantum analogue).
Now I want to make this precise.
To connect classical thermodynamics to probability theory, I’ll start by discussing ‘statistical manifolds’. I introduced the idea of a statistical manifold in Part 7: it’s a manifold equipped with a map sending each point
to a probability distribution
on some measure space
Now I’ll say how these fit into the second column of the above chart.
Then I’ll talk about statistical manifolds of a special sort used in thermodynamics, which I’ll call ‘Gibbsian’, since they really go back to Josiah Willard Gibbs.
In a Gibbsian statistical manifold, for each the probability distribution
is a ‘Gibbs distribution’. Physically, these Gibbs distributions describe thermodynamic equilibria. For example, if you specify the volume, energy and number of particles in a box of gas, there will be a Gibbs distribution describing what the particles do in thermodynamic equilibrium under these conditions. Mathematically, Gibbs distributions maximize entropy subject to some constraints specified by the point
More precisely: in a Gibbsian statistical manifold we have a list of observables whose expected values serve as coordinates
for points
and
is the probability distribution that maximizes entropy subject to the constraint that the expected value of
is
We can derive most of the interesting formulas of thermodynamics starting from this!
Statistical manifolds
Let’s fix a measure space with measure
A statistical manifold is then a manifold
equipped with a smooth map
assigning to each point
a probability distribution on
which I’ll call
So,
is a function on
with
and
for all
The idea here is that the space of all probability distributions on may be too huge to understand in as much detail as we’d like, so instead we describe some of these probability distributions—a family parametrized by points of some manifold
—using the map
This is the basic idea behind parametric statistics.
Information geometry is the geometry of statistical manifolds. Any statistical manifold comes with a bunch of interesting geometrical structures. One is the ‘Fisher information metric’, a Riemannian metric I explained in Part 7. Another is a 1-parameter family of connections on the tangent bundle which is important in Amari’s approach to information geometry. You can read about this here:
• Hiroshi Matsuzoe, Statistical manifolds and affine differential geometry, in Advanced Studies in Pure Mathematics 57, pp. 303–321.
I don’t want to talk about it now—I just wanted to reassure you that I’m not completely ignorant of it!
I want to focus on the story I’ve been telling, which is about entropy. Our statistical manifold comes with a smooth entropy function
namely
We can use this entropy function to do many of the things we usually do in thermodynamics! For example, at any point where this function is differentiable, its differential gives a cotangent vector
which has an important physical meaning. In coordinates we have
and we call the intensive variable conjugate to
For example if
is energy,
will be ‘coolness’: the reciprocal of temperature.
Defining this way gives a Lagrangian submanifold
of the cotangent bundle We can also get contact geometry into the game by defining a contact manifold
and a Legendrian submanifold
But I’ve been talking about these ideas for the last three episodes, so I won’t say more just now! Instead, I want to throw a new idea into the pot.
Gibbsian statistical manifolds
Thermodynamics, and statistical mechanics, spend a lot of time dealing with statistical manifold of a special sort I’ll call ‘Gibbsian’. In these, each probability distribution is a ‘Gibbs distribution’, meaning that it maximizes entropy subject to certain constraints specified by the point
How does this work? For starters, an integrable function
is called a random variable, or in physics an observable. The expected value of an observable is a smooth real-valued function on our statistical manifold
given by
In other words, is a function whose value at at any point
is the expected value of
with respect to the probability distribution
Now, suppose our statistical manifold is n-dimensional and we have n observables Their expected values will be smooth functions on our manifold—and sometimes these functions will be a coordinate system!
This may sound rather unlikely, but it’s really not so outlandish. Indeed, if there’s a point such that the differentials of the functions
are linearly independent at this point, these functions will be a coordinate system in some neighborhood of this point, by the inverse function theorem. So, we can take this neighborhood, use it as our statistical manifold, and the functions
will be coordinates.
So, let’s assume the expected values of our observables give a coordinate system on Let’s call these coordinates
so that
Now for the kicker: we say our statistical manifold is Gibbsian if for each point
is the probability distribution that maximizes entropy subject to the above condition!
Which condition? The condition saying that
for all i. This is just the previous equation spelled out so that you can see it’s a condition on
This assumption of the entropy-maximizing nature of is a very powerful, because it implies a useful and nontrivial formula for
It’s called the Gibbs distribution:
for all
Here is the intensive variable conjugate to
while
is the partition function: the thing we must divide by to make sure
integrates to 1. In other words:
By the way, this formula may look confusing at first, since the left side depends on the point in our statistical manifold, while there’s no
visible in the right side! Do you see what’s going on?
I’ll tell you: the conjugate variable sitting on the right side of the above formula, depends on
Remember, we got it by taking the partial derivative of the entropy in the
direction
and the evaluating this derivative at the point
But wait a minute! here is the entropy—but the entropy of what?
The entropy of of course!
So there’s something circular about our formula for To know
you need to know the conjugate variables
but to compute these you need to know the entropy of
This is actually okay. While circular, the formula for is still true. It’s harder to work with than you might hope. But it’s still extremely useful.
Next time I’ll prove that this formula for is true, and do a few things with it. All this material was discovered by Gibbs in the late 1800’s, and it’s lurking any good book on statistical mechanics—but not phrased in the language of statistical manifolds. The physics textbooks usually consider special cases, like a box of gas where:
• is energy,
is 1/temperature.
• is volume,
is –pressure/temperature.
• is the number of particles,
is chemical potential / pressure.
While these special cases are important and interesting, I’d rather be general!
Technical comments
I said “Any statistical manifold comes with a bunch of interesting geometrical structures”, but in fact some conditions are required. For example, the Fisher information metric is only well-defined and nondegenerate under some conditions on the map For example, if
maps every point of
to the same probability distribution, the Fisher information metric will vanish.
Similarly, the entropy function is only smooth under some conditions on
Furthermore, the integral
may not converge for all values of the numbers But in my discussion of Gibbsian statistical manifolds, I was assuming that an entropy-maximizing probability distribution
with
actually exists. In this case the probability distribution is also unique (almost everywhere).
For all my old posts on information geometry, go here:


Typos: You have a lot of unLaTeXed dollar signs in the last paragraph of the introduction and the first paragraph of the first section.
Whoops, and I was using some older notation I had for statistical manifolds. I fixed that. I’m trying to use for a statistical manifold now that I’m treating points
for a statistical manifold now that I’m treating points 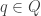 as analogous to points in a ‘configuration space’ in classical mechanics. This goes against the conventions in Part 3, but I’ll deal with that in the unlucky event that I turn this stuff into a book.
as analogous to points in a ‘configuration space’ in classical mechanics. This goes against the conventions in Part 3, but I’ll deal with that in the unlucky event that I turn this stuff into a book.
I see, the introduction had all the wrong letters originally! There's still an unLaTeXed $q \in Q$ in the last paragraph of the introduction and an unLaTeXed $Omega,$ in the first paragraph of the first section.
I think there might be a typo at the end: “I was assuming that an entropy-minimizing probability distribution \pi_q “. Do you mean maximizing? In the integral coming right after, is A missing a subscript (this also occurs earlier)?
Also, could you please go a bit more into the definition of Gibbsian in your next installment? I’m not understanding what’s assumed and what’s implied by the condition.
Thanks!
Thanks for catching those mistakes. I tried to fix them.
What don’t you get about the definition of Gibbsian? I defined it precisely – or so I thought. You may not be familiar with Gibbs distributions, so maybe I need to explain something that seems obvious to me. But you have to tell me what you’re puzzled by! It’s hard to help without knowing what’s the problem.
What I mainly plan to do next time is prove that the Gibbs distribution
maximizes the entropy
subject to the constraints that
for all i.
I guess I’m confused about what the q_{i} are supposed to be: you defined them starting from A_{i} and the distribution, but now you use them to define another distribution. So do we assume that we have coordinates q_{i} on Q and observables A_{i} on \Omega already, and then consider probability distributions for which the expectatin of A_{i} is q_{i}?
Francis wrote:
No, there’s only one distribution in this story: or more precisely, one map sending each point
sending each point  of a manifold
of a manifold  to a probability distribution
to a probability distribution 
Starting from this and some observables I defined the function
I defined the function
to be the expected value of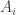 in the distribution
in the distribution  :
:
Then I assumed that the functions are a coordinate system on
are a coordinate system on  (and I explained why this is easy to achieve).
(and I explained why this is easy to achieve).
Then I made a big extra assumption: is the probability distribution with the largest possible entropy such that
is the probability distribution with the largest possible entropy such that
for all i. In other words: if you tell me the values of the coordinates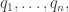 then
then  is not just any old probability distribution having these values as the expected values of the observables
is not just any old probability distribution having these values as the expected values of the observables  It’s the probability distribution with the largest possible entropy having these values as the expected values of the observables
It’s the probability distribution with the largest possible entropy having these values as the expected values of the observables 
I’m not changing here, I’m just making an extra assumption about it. This is a common assumption in thermodynamics.
here, I’m just making an extra assumption about it. This is a common assumption in thermodynamics.
Without this extra assumption there’s nothing very exciting we can do until someone tells us a formula for . But with this extra assumption I can show that
. But with this extra assumption I can show that  must obey this equation:
must obey this equation:
(I defined and
and 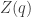 in the post.)
in the post.)
I will actually show this equation next time.
I hope the logic is clearer now. If there’s something puzzling still, just ask.
I added a bit about the traditional reasons for caring about Gibbsian statistical manifolds and the variables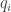 and
and  :
:
Great post! Question: what is the information analogue of FORCE?
Hi! That’s a good question. I will answer it someday, as I keep discussing the analogy between classical mechanics and information geometry. There are actually a few different possibilities, depending on what we take as the analogue of time.
It is pretty convoluted; I had to go through it a few times.
I think that it would help to use different symbols for (a point of the manifold
(a point of the manifold  ) and
) and 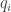 (a coordinate function on
(a coordinate function on  ). Because even though
). Because even though  can be written as a tuple using the coordinates
can be written as a tuple using the coordinates 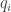 , still
, still  comes well before
comes well before 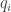 in the development.
in the development.
Everyone in differential geometry uses as coordinates of a point called
as coordinates of a point called 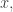 everyone in physics uses
everyone in physics uses 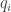 as coordinates of a position called
as coordinates of a position called  etc. This is confusing when you first see it, and you might feel tempted to write
etc. This is confusing when you first see it, and you might feel tempted to write  for the coordinate function
for the coordinate function  evaluated at the point
evaluated at the point  But it’s good to get used to.
But it’s good to get used to.
I’m sorry my exposition seemed convoluted. Maybe it’s because I was trying to explain two subjects in one blog post: statistical manifolds and thermodynamics. They’re closely related. In a statistical manifold each point labels a probability distribution. In thermodynamics each point of a manifold labels a probability distribution that maximizes entropy subject to constraints on some observables, and the expected values of these observables serve as coordinates.
I didn’t have a whole lot I wanted to say about statistical manifolds this time, except as a lead-in to thermodynamics. So I just laid out the basic formalism and then took a hard right turn into thermodynamics. If I ever turn this stuff into a book I’ll try to give the readers a more gentle ride.
Yes, but they do this when they start with the coordinates. Here the coordinates are derived at the end of a series of steps; I think that's adding to the confusion. I see why you did it this way, but it is an unusual order to do things.
Anyway, I'm really hoping that people who see these comments might think ‹Ah, that's why I'm confused, but now I understand.› rather than that you'll change the notation, especially since I don’t have a natural alternative to suggest.
Yeah. Socrates once complained that the problem with books is that you can’t ask a book questions. But on a blog you can ask questions — and other people can read the answers! This is what I like about blogs.
You might like
https://www.annualreviews.org/doi/full/10.1146/annurev-statistics-060116-054026
esp Fig 1.
That’s interesting, but I’m suspicious of it for some reason.