I’ve been thinking about chemistry lately. I’m always amazed by how far we can get in the study of multi-electron atoms using ideas from the hydrogen atom, which has just one electron.
If we ignore the electron’s spin and special relativity, and use just Schrödinger’s equation, the hydrogen atom is exactly solvable—and a key part of any thorough introduction to quantum mechanics. So I’ll zip through that material now, saying just enough to introduce the ‘Madelung rules’, which are two incredibly important rules of thumb for how electrons behave in the ground states of multi-electron atoms.
If take the Hilbert space of bound states of the hydrogen atom, ignoring electron spin, we can decompose it as a direct sum of subspaces:
where the energy equals in the subspace
Since the hydrogen atom has rotational symmetry, each subspace further decomposes into irreducible representations of the rotation group
Any such representation is classified by a natural number
Physically this number describes angular momentum; mathematically it describes the dimension of the representation. The angular momentum is
while the dimension is
Concretely, we can think of this representation as the space of homogeneous polynomials of degree
with vanishing Laplacian. I’ll say a bit more about this next time.
The subspace decomposes as a direct sum of irreducible representations with
like this:
So, in the subspace the electron has energy
and angular momentum
I’ve been ignoring the electron’s spin, but we shouldn’t ignore it completely, because it’s very important for understanding the periodic table and chemistry in general. To take it into account, all I will do is tensor with
to account for the electron’s two spin states. So, the true Hilbert space of bound states of a hydrogen atom is
By what I’ve said, we can decompose this Hilbert space into subspaces
called shells, getting this:
We can then decompose the shells further into subspaces
called subshells, obtaining our final result:
Since
the dimensions of the subshells are
or in other words, twice the odd numbers:
This lets us calculate the dimensions of the shells:
since the sum of the first bunch of odd numbers is perfect square. So, the dimensions of the shells are twice the perfect squares:
Okay, so much for hydrogen!
Now, the ‘Aufbau principle’ says that as we keep going through the periodic table, looking at elements with more and more electrons, these electrons will act approximately as if each one occupies a subshell. Thanks to the Pauli exclusion principle, we can’t put more electrons into some subshell than the dimension of that subshell. So the big question is: which subshell does each electron go into?
This is the question that the Madelung rules answer! Here’s what they say:
- Electrons are assigned to subshells in order of increasing values of
.
-
For subshells with the same value of
, electrons are assigned first to the subshell with lower
—or equivalently, higher
They aren’t always right, but they’re damned good, given that in reality we’ve got a bunch of electrons interacting with each other—and not even described by separate wavefunctions, but really one big fat ‘entangled’ wavefunction.
Here’s what the Madelung rules predict:
So, subshells get filled in order of increasing and for any choice of
we start with the biggest possible
and work down.
This chart uses some old-fashioned but still very popular notation for the subshells. We say the number but instead of saying the number
we use a letter:
• : s
• : p
• : d
• : f
The reasons for these letters would make for a long and thrilling story, but not today.
The history of the Madelung rules
At this point I should go through the periodic table and show you how well the Madelung rules predict what’s going on. Basically, as we fill a particular subshell we get a bunch of related elements, and then as we go on up to the next subshell we get another bunch—and we can understand a lot about their properties! But there are also plenty of deviations from the Madelung rules, which are also interesting. I’ll talk about all these things next time.
I should also say a bit about why the Madelung rules work as well as they do! For example, what’s the importance of
But that’s not what I have lined up for today. Sorry! Instead, I want to talk about something much less important: the historical origin of the Madelung rules. According to Wikipedia they have many names:
• the Madelung rule (after Erwin Madelung)
• the Janet rule (after Charles Janet)
• the Klechkowsky rule (after Vsevolod Klechkovsky)
• Wiswesser’s rule (after William Wiswesser)
• the Aufbau approximation
• the diagonal rule, and
• the Uncle Wiggly path.
Seriously! Uncle Wiggly!
Understanding the history of these rules is going to be difficult. You can read a lot about their prehistory here:
• Wikipedia, Aufbau principle.
Bohr and Sommerfeld played a big role in setting up the theory of shells and subshells, and perhaps the whole idea of ‘Aufbau’: German for ‘building up’ atoms one electron at a time.
But I was confused about whether Madelung discovered both rules or just one, especially because a lot of people say ‘Madelung rule’ in the singular, when there are really two. So I asked on History of Science and Mathematics Stackexchange:
There are two widely used rules of thumb to determine which subshells are filled in a neutral atom in its ground state:
• Electrons are assigned to subshells in order of increasing value of
.
• For subshells with the same value of
, electrons are assigned first to the subshell with lower
.
These rules don’t always hold, but that’s not my concern here. My question is: which of these rules did Erwin Madelung discover? (Both? Just one?)
Wikipedia seems to say Charles Janet discovered the first in 1928:
A periodic table in which each row corresponds to one value of
(where the values of
and
correspond to the principal and azimuthal quantum numbers respectively) was suggested by Charles Janet in 1928, and in 1930 he made explicit the quantum basis of this pattern, based on knowledge of atomic ground states determined by the analysis of atomic spectra. This table came to be referred to as the left-step table. Janet “adjusted” some of the actual
values of the elements, since they did not accord with his energy ordering rule, and he considered that the discrepancies involved must have arisen from measurement errors. In the event, the actual values were correct and the
energy ordering rule turned out to be an approximation rather than a perfect fit, although for all elements that are exceptions the regularised configuration is a low-energy excited state, well within reach of chemical bond energies.
It then goes on to say:
In 1936, the German physicist Erwin Madelung proposed this as an empirical rule for the order of filling atomic subshells, and most English-language sources therefore refer to the Madelung rule. Madelung may have been aware of this pattern as early as 1926.
Is “this” still rule 1?
It then goes on to say:
In 1945 William Wiswesser proposed that the subshells are filled in order of increasing values of the function
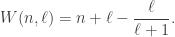
This is equivalent to the combination of rules 1 and 2. So, this article seems to suggest that rule 2 was discovered by Wiswesser. But I have my doubts. Goudsmit and Richards write:
Madelung discovered a simple empirical rule for neutral atoms. It consists of two parts.
and then they list both 1 and 2.
I have not yet managed to get ahold of Erwin Madelung’s work, e.g.
• E. Madelung, Die mathematischen Hilfsmittel der Physikers, Springer, Berlin, 1936
I got a helpful reply from M. Farooq:
The only relevant section in E. Madelung’s edited book, Die mathematischen Hilfsmittel der Physikers, Springer: Berlin, 1936 is a small paragraph. It seems Madelung just called this for electron book-keeping and he had no justification for his proposition. He calls it a lexicographic order (lexikographische Ordnung).
I was searching for it some other reasons several months ago: Question in SE Physics. The original and the (machine but edited) translations is shared.

15 Atomic structure (electron catalog) (to p. 301).
The eigenfunction of an atom, consisting of
electrons and
-times positively charged nucleus, can be constructed in the case of removed degeneracy in first approximation as a product of
hydrogen eigenfunctions (cf. p. 356), each of which is defined by four quantum numbers
defined by
. According to Pauli’s principle, no two of these functions may coincide in all four quantum numbers. According to the Bohr principle of structure, an atom with
electrons is formed from an atom with
electrons by adding another one (and increasing the nuclear charge by 1) without changing the quantum numbers of the already existing electrons. Therefore a catalog can be set up, from whose in each case
first positions the atom is built up in the basic state (cf. the table p. 360).
The ordering principle of this catalog is a lexicographic order according to the numbers
A theoretical justification of just this arrangement is not yet available. One reads from it:
1. The periodic system of the elements. Two atoms are homologous if in each case their “last electron” in the
coincides.
2. The spectroscopic character of the basic term, entered in column 10 . There is namely
the character
and
the multiplicity.
3. The possibilities for excited states (possible terms), where not all
electrons are in the first
positions of the catalog.
The catalog is the representation form of an empirical rule. It idealizes the experience, because in some cases deviations are observed.
So, it’s clear that Madelung knew and efficiently stated both rules in 1936! By the way, ‘lexicographic order’ is the standard mathematical term for how we’re ordering the pairs in the Madelung rules.
References
I took the handsome chart illustrating the Madelung rules from here:
• Aufbau Principle Chemistry God, 18 February 2020.
This blog article is definitely worth reading!


Did you know how to modify this rule when the number of space-time dimensions change? There are some papers about periodic tables in Flatland and Higher Dimensions. Have you read about it? I am sure a mathematician like you would enjoy the higher/lower dimensional versions of the Periodic Table and Madelung rule. By the way, any relation of the above facts with the harmonic oscillator?
Ehrenfest has a nice paper about why atoms can no exist in 5 or higher dimensions in stable forms. However, there are some caveats that have been discussed decades after him. As far as I know, it is a controversial topic too.
No, I haven’t read about those modified periodic tables. I could say a lot about how things work when you have a bunch of noninteracting quantum-mechanical particles attracted to a much heavier point nucleus in space dimensions by a
space dimensions by a  force (or a constant attractive force when
force (or a constant attractive force when  ). Maybe you know that stuff already.
). Maybe you know that stuff already.
But the Madelung rules can only be understood by considering the interactions between the particles orbiting the nucleus—that is, the repulsive electrostatic force between electrons. When we take these into account the problem ceases to be exactly solvable. Then the Madelung rules show up! But they are not at all easy to derive in the usual case, and indeed they’re not always true — the first breakdown of the rules as I stated them occurs in chromium, the second in copper, etc. So, it would be challenging to see what happens in other dimensions.
case, and indeed they’re not always true — the first breakdown of the rules as I stated them occurs in chromium, the second in copper, etc. So, it would be challenging to see what happens in other dimensions.
But maybe someone has studied this—and if not, someone may. If our civilization doesn’t collapse, eventually people will seriously study chemistry under various modified laws of physics. The dimension of space is one of the most obvious things to vary.
Even in the “real world” case (3D) the interaction of electrons makes the calculation really hard. as the fact there there is no analytical solution for helium atom case (2 electrons, disregarding SR). Perhaps there are numerical solutions for it. I simply do not know. I would love to see all numerical analyses being done for all elements, but I read somewhere that such calculations can bring a supercomputer to its knees, Oh well…
Helium is quite well understood: go here and read all the way down:
• Wikipedia, Helium atom: the perturbation method and the variational method.
I should learn more about the state of the art with multi-electron atoms. Note that computing the ground state of, say, iron amounts to figuring out a function of 78 real variables valued in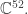 It’s probably more practical to compute things like the spectrum of iron, which you can compare against experiment.
It’s probably more practical to compute things like the spectrum of iron, which you can compare against experiment.
The helium ground state was “done” by Hyleraas in quasi analytical precision. The problem are the electron-electron interaction (replusion) terms that prohibit a product ansatz (direct sum) of the solution.
Yes! I knew it! And yes…I mentioned Pekka Pykko because he has of course written about why gold and other elements have those anomalous electronic configurations violating the Madelung rules. As a physicist, and physics and chemistry HS teacher right now to survive, I know that relativistic corrections to some elements do in fact alter the semi-empirical and “rule-of-thumb” of Madelung’s. Also, I suppose you know that the technetium is another curious “accident” of the Periodic Table in 3d. It yields that ekamanganese or technetium is (quantum). I you have really time, Pekka Pykko works are really cool in spare time (if any).
Another interesting issue, I think you wrote about that in your TWF or you mentioned it in the past, is the issue of “the last element”. Let it be feynmannium, element 172 (Greiner et al.) or “no last element”, it is surely a question for the next physicists and chemists to handle with.
I am well aware of your fear of civilization collapse. I also have it. But maybe, future generations will read these lines and other registers, and will find a way to survive. Otherwise, my biggest fear beyond don’t be a Doctor or find a corresponding geek female who love me as I do, the reason to solve the Fermi paradox would be dramatic and simple: it is very hard to become not even an interstellar, intergalactic, multiversal civilization, it is even hard to have enought time to survive and not to self-destroy…Even, we have been fortunated enough to see not a big asteroid in 65Myr, a near supernova, a primordial BH crossing Earth, and many other menaces.
Said this, please John. You are a great blogger. Don’t be pessimistic despite the risk and evidences of collpase. We need hope. And we will always need scientists like you and many other sharing your thoughts and knowledge, spreading in all you can.
The violations of the direct sum Hilbert space model kicks in much earlier, already in the transition block elements you start to feel the inter-electronic correlation, in the atomic levels of copper (Cu) for example.
For a strong attack on the Madelung rules, see:
• Eric Scerri, The problem with the aufbau principle for finding electronic configurations, 24 June 2012.
But it’s important to realize that he’s attacking a version of the Madelung rules that is different, and strong than the version stated in my blog article! The version in my blog article is only about atoms, not ions. The stronger version claims that you can use the Madelung rules not only to determine the ground state of a neutral atom, but also the positive ions obtained by removing some electrons!
This stronger version breaks down if you consider scandium with one electron removed. Scandium has the electrons as in argon together with three more, two in the 4s orbital and one in the 3d orbital. This conforms to the Madelung rules, which say 3d comes after 4s:
But when you ionize scandium and remove one electron, it’s not the 3d electron that leaves—it’s one of the 4s electrons! This breaks the stronger version of the Madelung rules.
The version of the Madelung rules stated in my blog also breaks down, but only later, with chromium, copper, etc.
Great work, John, thanks a lot! It will be my reference when ever a Mathematician asks ma about atomic energy levels, the PSE and the Aufbauprinciple.
Thanks!
P.S.: A simple look to the great page of Pekka Pykko for you and others who read your magnificent blog… It’s WORTHY! http://www.chem.helsinki.fi/~pyykko/
P.S.(II): Interacting! Yes, Madelung’s rule is changed with the effects of…RELATIVISTIC quantum mechanics. Indeed, features of mercury and gold (or silver) can only be understood as an special relativity correction to the Madelung’s rule. Pekka Pykko’s work shows with his extended periodic table (via numerical solution to the relativistic field equation of those multielectrons) that beyond 122, there are some weird ubications of some elements in the “extended” periodic table. I will likely be dead (if humaninty survives) when we began to produce g-elements to understand the cool chemistry it seems they are going to provide. (Special) Relativistic quantum chemistry!!!!!!
In a comment John said: “I should learn more about the state of the art with multi-electron atoms.”
I can’t help you there, except to say that I knew papers like this must exist before looking.
Learning Full Configuration Interaction Electron Correlations with Deep Learning
https://arxiv.org/abs/2106.08138
What is the attitude among physicists to this sort of approach?
I’ve vaguely heard about the sort of obvious controversy, but I’m very far from the people who really care about these things. I imagine machine learning is most acceptable if you really want answers to questions, don’t much mind if there’s a chance they’re wrong, and don’t care too much about why the answers are true.
My interest in multi-electron atoms is completely different: I have no practical interest in them, all I’m curious about is the extent to which we can understand the ground states of atoms from first principles, using Schrödinger’s equation.
Let me add another point about what reason has a physicist (like me), even if theoretical and mathematician-like, has with multi-electron physics: superconductivity and exotic phases of matter (or even more: exotic “space-times” if we make a dual of these materials into spacetime physics). Despite all the effort, we are yet puzzled by the physics of high-T superconductivity. Recent advances have come in different ways, not in the part of theory as far as I know:
-Magic angles and role in superconductors like graphene sheets.
-Ultra high pressure high-T temperature. Speculated long ago with the hydrogen in metal phase, several studies with ultra high pressure compounds such as H3S or LaH_x have pushed the research on the ultimate theory of high superconductor materials.
Ultimately, even if BCS theory survive at the level of a modified version for High-T superconductors or exotic superconductivity being found these days, the thing is that superconductivity is likely something to do with how electrons in different orbitals interact (or lack interaction/resistivity). I am yet wishing for some new fresh idea of why or how could be understand high-T superconductors and made high-T superconductors…Imagine to transport energy without losses… And yet, it seems there is much to do with the theory part, …Despite the fact sometimes believe that, it is more and more likely that the theory of high-T superconductors will be done by AI if not good theorists do good work on it the next decade… Of course, I can be wrong and a sudden discovery in this field could revolutionize the whole subject…We live interesting times!
Have you looked at this?
• Jan Zaanen, Lectures on quantum supreme matter.
Does it make sense?
After reading again this article, I found this reading
Click to access TFG_Jordi_Llusar_Camarelles.pdf
Interesting stuff about 2D vs. 3D electronic stuff. And much more. I just remember when John suggested time ago to simulate materials in 2D and I believe higher dimensions as models of Universes for both mathematicians and physicists in condensed matter theory. Certainly, with the rise of AI, Machine Learning and other tools, it will be a fruitful interdisciplinary field this century and beyond.
(Typo: where you have , that should be
, that should be 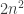 .)
.)
I’ve never taken a chemistry course, perhaps mainly because I didn’t complete high school, but I’m interested in learning some fundamental chemistry like explaining the structure of the periodic table. Naive question: what’s the meaning behind the energies being negative?
Thanks for catching that mistake! Fixed.
For starters, what does “zero energy” mean?
In many branches of physics, including atomic physics, the concept of zero energy is arbitrary, in that we can add a constant to our definition of energy without changing anything observable. So, we choose the zero in a convenient way. Say you have an electron very far from a proton, not moving much. Then its energy is defined to be near zero.
(In the limit where it gets farther and farther away, and it’s moving slower and slower, we say its potential and kinetic energy both approach zero. In classical mechanics its velocity can be exactly zero, but in quantum mechanics we can only approach that situation, never quite reach it.)
Okay, so now about “negative energy”.
If the electron gets near the proton it’s attracted and “falls down the potential well”, and then it will have negative energy. In the process it will release radiation that carries away the equal and opposite amount of positive energy.
In other words, and perhaps more convincingly: if you have an electron orbiting a proton, it takes positive energy to “yank it out” and make it into an electron that’s far from the proton, not moving much.
A much deeper fact is the virial theorem, which says that for a particle orbiting in an inverse square attractive force, its average potential energy is -2 times its average kinetic energy.
For an electron in hydrogen in the nth energy eigenspace, which I called here, its kinetic energy is
here, its kinetic energy is  (in some units) while its potential energy is
(in some units) while its potential energy is  so its energy is
so its energy is 
Thank you! The intuition of the far-away electron was helpful.
I also learned that the virial theorem was what Zwicky used to infer the presence of dark matter, back in the 30’s.
I show accurate electron configurations on Ptable with Madelung exceptions in red, but I also want to fan out ions the way I do on the Isotopes tab, and then show all their configurations as well. Is Fe 2+ going to be the same, with an exception, as Cr, or should all ions be calculated as strict Madelung, or something in between?