Part 1 introduced the ‘binary octahedral group’. This time I just want to show you some more pictures related to this group. I’ll give just enough explanation to hint at what’s going on. For more details, check out this webpage:
• Greg Egan, Symmetries and the 24-cell.
Okay, here goes!
You can inscribe two regular tetrahedra in a cube:
Each tetrahedron has 4! = 24 symmetries permuting its 4 vertices.
The cube thus has 48 symmetries, twice as many. Half map each tetrahedron to itself, and half switch the two tetrahedra.
If we consider only rotational symmetries, not reflections, we have to divide by 2. The tetrahedron has 12 rotational symmetries. The cube has 24.
But the rotation group SO(3) has a double cover SU(2). So the rotational symmetry groups of tetrahedron and cube have double covers too, with twice as many elements: 24 and 48, respectively.
But these 24-element and 48-element groups are different from the ones mentioned before! They’re called the binary tetrahedral group and binary octahedral group—since we could have used the symmetries of an octahedron instead of a cube.
Now let’s think about these groups using quaternions. We can think of SU(2) as consisting of the ‘unit quaternions’—that is, quaternions of length 1. That will connect what we’re doing to 4-dimensional geometry!
The binary tetrahedral group
Viewed this way, the binary tetrahedral group consists of 24 unit quaternions. 8 of them are very simple:
These form a group called the quaternion group, and they’re the vertices of a shape that’s the 4d analogue of a regular octahedron. It’s called the 4-dimensional cross-polytope and it looks like this:
The remaining 16 elements of the binary tetrahedral group are these:
They form the vertices of a 4-dimensional hypercube:
Putting the vertices of the hypercube and the cross-polytope together, we get all 8 + 16 = 24 elements of the binary tetrahedral group. These are the vertices of a 4-dimensional shape called the 24-cell:
This shape is called the 24-cell not because it has 24 vertices, but because it also has 24 faces, which happen to be regular octahedra. You can see one if you slice the 24-cell like this:
The slices here have real part 1, ½, 0, -½, and -1 respectively. Note that the slices with real part ±½ contain the vertices of a hypercube, while the rest contain the vertices of a cross-polytope.
And here’s another great way to think about the binary tetrahedral group. We’ve seen that if you take every other vertex of a cube you get the vertices of a regular tetrahedron. Similarly, if you take every other vertex of a 4d hypercube you get a 4d cross-polytope. So, you can take the vertices of a 4d hypercube and partition them into the vertices of two cross-polytopes.
As a result, the 24 elements of the binary tetrahedral group can be partitioned into three cross-polytopes! Greg Egan shows how it looks:
The binary octahedral group
Now that we understand the binary tetrahedral group pretty well, we’re ready for our actual goal: understanding the binary octahedral group! We know this forms a group of 48 unit quaternions, and we know it acts as symmetries of the cube—with elements coming in pairs that act on the cube in the same way, because it’s a double cover of the rotational symmetry group of the cube.
So, we can partition its 48 elements into two kinds: those that preserve each tetrahedron in this picture, and those that switch these two tetahedra:
The first 24 form a copy of the binary tetrahedral group and thus a 24-cell, as we have discussed. The second form another 24-cell! And these two separate 24-cells are ‘dual’ to each other: the vertices of each one hover above the centers of the other’s faces.
Greg has nicely animated the 48 elements of the binary octahedral group here:
He’s colored them according to the rotations of the cube they represent:
• black: identity
• red: ±120° rotation around a V axis
• yellow: 180° rotation around an F axis
• blue: ±90° rotation around an F axis
• cyan: 180° rotation around an E axis
Here ‘V, F, and E axes’ join opposite vertices, faces, and edges of the cube.
Finally, note that because
• we can partition the 48 vertices of the binary octahedral group into two 24-cells
and
• we can partition the 24 vertices of the 24-cell into three cross-polytopes
it follows that we can partition the 48 vertices of the binary octahedral group into six cross-polytopes.
I don’t know the deep meaning of this fact. I know that the vertices of the 24-cell correspond to the 24 roots of the Lie algebra 
All I know is that if you pick a quaternion group sitting in the binary octahedral group, it will have 6 cosets, and these will be six cross-polytopes.
Azimuth 
“the the [sic] famous ‘triality’ symmetry of
permutes the three cross-polytopes in the 24-cell, which are in some rather sneaky way related to the three 8-dimensional irreducible representations of 
.”
This part is not sneaky. The cross-polytope arises very obviously as the weights of so(8)’s maximal torus
acting on the standard representation 
. This is most easily seen if we define 
where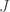 
is the identity matrix flipped left-right, and 
.
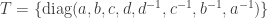I’ll admit to being confused as to how the 24 roots (the weights of the adjoint representation, which is the fundamental rep corresponding to the central vertex in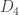
) are supposed to relate to the weights of the three other fundamental representations. Basically, you should be able to take any one of them (say, the standard rep above) and consider its 
as the adjoint rep. But it’s not clear to me whether, much less “why”, the vector configuration of the 24 roots is isomorphic to that of the weights of the direct sum of the three minuscule representations.
Allan wrote:
Yeah, that’s what I’m calling “sneaky”. If I start by thinking of the 24-cell’s vertices as the 24 roots of
it’s a fact that we can partition these into the vertices of 3 cross-polytopes that are permuted by triality. But the vertices of these 3 cross-polytopes must be rescaled and maybe also rotated versions of the weights of the three 8-dimensional irreps of 
So I think we agree on what’s confusing here.
If I understood this, I might be able to take the direct sum of all three of those 8-dimensional irreps, which I can identify with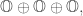
and give it a natural Lie algebra structure making it isomorphic to 
.
Or I might learn why this is a bad idea.
OK here’s what it sounds like could be happening, but it also sounds crazy.
Let G,H both be
(I could work with Lie algebras but no thanks. To get all the irreps we need, though, I need the simply-connected group). Consider G acting on the sum of the three minuscule irreps, which it does faithfully, and H acting on the adjoint representation, which kills its center (a Klein Viergruppe, meaning “little group of fear”).
Then the combinatorics you want might come from having a homomorphism of H’s torus onto G’s torus, killing that center. The reason I find this crazy is that it doesn’t come from a homomorphism of H to G.
According to my calculations, these two 24-element vector configurations are indeed isomorphic, after a rescaling. Specifically, we can take the weights (1000), (0100), (0010) from the standard representation and the weight (-1,-1,-1,1)/2 from the spin representation to the simple roots.
One question would be whether this homomorphism of tori extends to larger subgroups of G,H (although not to the whole thing). There’s an intriguing group SU(2)^4/Z_2 lying over the SO(4) x SO(4) inside the quotient SO(8).
Can you describe this isomorphism/rescaling a bit more explicitly? I’d like to see 4 vectors that span a lattice L, and 4 other vectors that span a sublattice L’, with L’ being a rescaled version of L, and L/L’ being the Klein 4-group. You’re sort of partially describing this and assuming I remember the rest. I guess you’re listing generators for L.
The four vectors I listed are a basis for my weight lattice L. Inside that lattice are the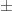
basis vectors, giving the weights of the standard representation. The Z/3 triality action is given by the matrix
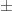the rows of that, and of the spin_- rep, 
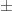the rows of its square.
i.e. the weights of the spin_+ rep are
Meanwhile the roots are permutations of (+,-,0,0),(+,+,0,0). We can take (+-00), (00+-), (00++), (0+-0) as our simple roots, spanning L’. The matrix
taking the weight lattice basis (rows of W) to the root lattice basis (rows of R) is
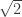times an orthogonal matrix.
which is
Up to reordering the rows, this is a sum of two copies of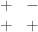
, whose image is the black squares on the checkerboard, i.e. whose cokernel is Z/2. Hence L/L’ is the Viergruppe.
Oops, the matrix I gave for triality has to be divided by 2.
I think the following is the (not especially) general statement. Let G be a non-simply-laced simple group (here F_4). Then the short roots of G, as a vector configuration, match (up to scale) the long roots of the Langlands dual of G. If that’s the same Dynkin diagram (the F,G cases, not the B,C cases) then one might mistake them for the long roots of G. Representation-theoretically we should consider H the subgroup of G corresponding to the long roots, and decompose the adjoint rep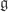
under H: one piece is the adjoint rep 
with the long roots and zero, and the remainder is a bunch of H-irreps.
Inside F_4 is B_4, inside B_4 is D_4, and when we decompose the adjoint rep of F_4 under this D_4 we get the adjoint rep of D_4 plus (I’m reasonably sure) the three minuscules.
The other case, G_2 containing A_2, is easier to draw
https://en.wikipedia.org/wiki/G2_(mathematics)#/media/File:Root_system_G2.svg
where the short roots decompose into the two fundamental reps of A_2 = SU(3).
Slight refinement of the statement. There is a Z/2 x Z/2 inside F_4, and if one decomposes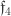
under that Viergruppe, the four isotypic components are 
(the trivial part) and the three minuscules. (If you add the trivial part to one of the other pieces, you get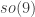 
.) What’s interesting is that the Z/3 triality action is inner for F_4, so I guess there’s an Alt(4) inside F_4, the semidirect product of that Z/3 and the Viergruppe. That sounds like one of the finite subgroups Serre was all het up around the turn of the century.
Aaand of course the Weyl group of F_4 is the automorphism group of the 24-cell (Wikipedia). I guess the obvious part is that W(F_4) acts on the convex hull of the root system; if there were more automorphisms, they’d give outer automorphisms of F_4. But its Dynkin diagram has no symmetries, so there are no outer automorphisms. (Which is exactly what goes wrong if one says “the 24-cell is the convex hull of D_4’s roots, so W(D_4) acts on the 24-cell”.)
This can’t quite be complete, though, since B_4 has no symmetries but W(B_4) doesn’t give the full automorphism group.
Under the sentence that starts with “Greg has nicely animated the 48 elements of […]”, the “picture” appears as a blank on my Firefox browser. The link to Greg Egan webpage works though. Thought to let you know, especially since you put the description of the parts below that picture and I have no clue how it looks.
I don’t have that problem myself. It’s an 18-megabyte animated gif, and it’s available on Greg’s webpage and also here:
https://math.ucr.edu/home/baez/mathematical/binary_octahedral_group.gif
I had that problem today, so I fixed it using a hack.
Beautiful! Thanks Greg and John.
Thanks!