Light can bounce off light by exchanging virtual charged particles! This gives nonlinear corrections to Maxwell’s equations, even in the vacuum—but they’re only noticeable when the electric field is about 1018 volts/meter or more. This is an enormous electric field, able to accelerate a proton from rest to Large Hadron Collider energies in just 5 micrometers!
In 2017, light-on-light scattering was seen at the LHC when they shot lead ions past each other:
Direct evidence for light-by-light scattering at high energy had proven elusive for decades, until the Large Hadron Collider (LHC) began its second data-taking period (Run 2). Collisions of lead ions in the LHC provide a uniquely clean environment to study light-by-light scattering. Bunches of lead ions that are accelerated to very high energy are surrounded by an enormous flux of photons. Indeed, the coherent action from the large number of 82 protons in a lead atom with all the electrons stripped off (as is the case for the lead ions in the LHC) give rise to an electromagnetic field of up to 1025 volts per metre. When two lead ions pass close by each other at the centre of the ATLAS detector, but at a distance greater than twice the lead ion radius, those photons can still interact and scatter off one another without any further interaction between the lead ions, as the reach of the (much stronger) strong force is bound to the radius of a single proton. These interactions are known as ultra-peripheral collisions.
But now people want to see photon-photon scattering by shooting lasers at each other! One place they’ll try this is at the Extreme Light Infrastructure.
In 2019, a laser at the Extreme Light Infrastructure in Romania achieved a power of 10 petawatts for brief pulses — listen to the announcement for what means!
I think it reached an intensity of 1029 watts per square meter, but I’m not sure. If you know the intensity 
where 
In China, the Station of Extreme Light plans to build a laser that makes brief pulses of 100 petawatts. That’s 10,000 times the power of all the world’s electrical grids combined—for a very short time! They’re aiming for an intensity of 1028 watts/square meter:
• Edwin Cartlidge, Physicists are planning to build lasers so powerful they could rip apart empty space, Science, January 24, 2018.
The modification of Maxwell’s equations due to virtual particles was worked out by Heisenberg and Euler in 1936. (No, not that Euler.) They’re easiest to describe using a Lagrangian, but if we wrote out the equations we’d get Maxwell’s equations plus extra terms that are cubic in 
For more, read these:
• Wikpedia, Schwinger limit.
• Wikpedia, Schwinger effect.
The Schwinger limit is the strength of the electric (or magnetic) field where nonlinearity due to virtual charrged particles becomes significant. They’re about
where 
• David Delphenich, Nonlinear electrodynamics and QED.
The Schwinger effect is when a very large static electric field ‘sparks the vacuum’ and creates real particles. This may put an upper limit on many protons can be in an atomic nucleus, spelling an end to the periodic table.
Azimuth 
So Maxwell is non-linear? Shades of EFE.
Everything is linear to first order, but beyond that you’re on your own… and very few things, if any, are exactly linear.
Everything, eh? Does that mean that the quantum state space isn’t linear either? If so, what mathematical entity could replace the linear space to make it nonlinear but almost linear?
I said “very few things, if any, are linear”, not “nothing is linear”. Quantum theory could be one of the few things in nature that’s perfectly linear. In 1989 Weinberg wrote a couple of papers considering the possibility of small deviations from linearity in quantum theory and how we could detect them experimentally. I don’t know how hard people have looked—I haven’t found any papers by people doing these experiments!—but obviously nobody has found any deviations yet.
Is that related to Penrose‘s ideas about gravity affecting quantum mechanics?
Penrose has done some excellent stuff: singularity theorems, irregular tiling, and so on. His latest cosmology speculations haven‘t really convinced many, and hardly anyone believes in his quantum-consciousness stuff.
But his gravity-could-affect-quantum-mechanics stuff seems reasonable, at least at first glance. I suspect that most suspect that GR but perhaps not QM will have to be modified for quantum gravity.
I believe Weinberg just proposed a simple framework to describe small deviations from linearity in (some applications of) quantum mechanics, a bit like how the parametrized post-Newtonian formalism lets us describe small deviations from Newtonian gravity, so we can organize experiments to compare general relativity against other theories. But this is just my impression—I’ve never studied his work! I’m pretty sure neither he nor Penrose came up with a detailed theory describing small nonlinear deviations from quantum mechanics.
If an expert on this subject reads this, please chime in!
“Station of Extreme Light” made my (admittedly otherwise rather pedestrian) day, thanks😊
If you worked at the Station of Extreme Light, your days would be brighter.
Sounds like one of those (then) new southern-California religions back in the 1960s founded by someone who, in the words of Kirk, took too much LDS.
The analyst Elliot Lieb, cf eg
Large atoms in the magnetic field of a neutron star.
Spectral and scattering theory and applications, 259–273,
Adv. Stud. Pure Math., 23, Math. Soc. Japan, Tokyo, 1994.
has done a lot of interesting work on extreme states of matter…
Sometime I should check those out!
A factor of 2/45 in the Euler-Heisenberg Lagrangian, and then a 7. You have to love it.
You have to love it, or it makes you angry.
I would like to understand those numbers! There’s a lot of interesting number theory hiding in the evaluation of Feynman diagrams.
John Donoghue and coauthors computed the quantum corrections to the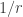
potential for gravity using perturbative quantum gravity and got
The first correction is due to general relativity; the next one is really a quantum gravity effect.
About Feynman diagrams: it is really SICK how precise and exact they can be. I believe the hidden symmetries of role in QFT are yet to be fully unveiled. In fact, there are some works relating Feynman graphs with number theory (to be more precise, polylogarithms, elliptic polylogarithms and other strange generalized functions; that the Apery constant appears indeed in recent works related to that, and with connections to the amplituhedron and similar structures, not only with string amplitudes, reveal a yet to uncover relationship between number theory, algebraic geometry and the physics of amplitudes of high energy physics that stumbles me so much as its complexity, beauty and …order). However, I admit myself to be a complete nut about the new research on periods of feynman graphs in QFT. I am yet expecting a good review paper to upgrade my knowledge of that subject…The Riemann Hypothesis also waits for such development (I think the proof of RH could also involve some hint of connections not only with Dirichlet L-functions, but also with the structure of QFT and Feynman graphs). Maybe this century and the following will develop abstract algebraic structures to be used in the TOE. I feel non-archimedian analysis could be playing a higher role in physics at the end point…However, I am not updraded of p-adic QFT studies in holography that I really want to read this Christmas…
By the way, another really interesting, analogous scattering event is
photon+photon -> matter
which was only observed in the last few years:
https://phys.org/news/2020-09-lhc.html
I’m reading your blog through an feed reader, thus I probably don’t show up in the weblog statistics… so I’m writing to thank you for all the great posts over the years. I usually lose you after the second formula or so, but greatly appreciate the layman-digestible intros.
Great! You can also try ignoring the formulas and reading the words. Maybe that’s unpleasant, but most of the time I try to say everything in words; the equations are supposed to say the same thing a bit more precisely.