This is a continuation of my post Dividing a square into similar rectangles, in which I discussed this puzzle: if you partition a square into n similar rectangles, what proportions can these rectangles have?
Some people on Mathstodon put a lot of work into this and made some nice progress. But there’s been a surprising new twist! I’m not talking about how the answer to this puzzle is now listed on the listed on the Online Encyclopedia of Integer Sequences as sequence A359146. I’m not even talking about the fact that the New York Times ran an article about this puzzle:
• Siobhan Roberts, The quest to find rectangles in a square, New York Times, February 7, 2023. Open-access version here.
Remember the story so far. When n = 3 there are just 3 options for what the proportions of the rectangles can be:
I asked folks on Mathstodon about the case n = 4 and they found 11 options, as drawn here by Dan Piker:
From then on the number increases steeply. The biggest case anyone has been able to handle is n = 7. Ian Henderson found 1371 options in that case:
And that was great… but now the story has gotten more interesting, because Daniel Gerbet seems to have found one more! Yes: not 1371, but 1372.
He did the computation twice, in two different ways. He sent me a table listing all 1372 allowed proportions in increasing order, together with the polynomial equations they obey and pictures of the subdivided square. He wrote:
After running the computation again, I was able to identify the possibly missing guy exactly: the 1055th ratio. The pictures of the partitions look all the same for smaller and larger ratios in the tables from Ian Henderson and the one I computed. You find it at page 106 in the tabletable for partitions with 7 rectangles.
The ratio is the only real root of the polynomial
You can find a picture of a partition with this ratio in the files attached. Note that Ian Henderson has computed partitions with other ratios, but the same topology as this one, e.g. the 1022th ratio.
Indeed it’s an interesting fact, first noted by Lisanne Taams in a simpler example, that we can get two partitions with the same topology where the rectangles have different proportions!
Here is a picture of the apparently new partition that Daniel Gerbet has found:
You can also see it as the 1055th partition in this list, where the 1372 partitions are conveniently grouped into 25 groups of 54, plus 22 more:
I said “conveniently”, but of course I was kidding—it’s easier to deal with these pictures in a PDF file. Daniel Gerbet has kindly allowed me to share his PDFs for all the interesting cases up to n = 7:
• All 3 allowed proportions for 3 similar rectangles that subdivide the square.
• All 11 allowed proportions for 4 similar rectangles that subdivide the square.
• All 51 allowed proportions for 5 similar rectangles that subdivide the square.
• All 245 allowed proportions for 6 similar rectangles that subdivide the square.
• All 1372 allowed proportions for 7 similar rectangles that subdivide the square. Also, don’t forget the more detailed table listing the polynomials obeyed by these proportions.
You can also get a copy of the Python program that Daniel Gerbet used to obtain his results.
By the way, when I mentioned this news to my friend Todd Trimble he instantly noticed that 1372 is divisible by 7. Coincidence? Probably.
Some good news here is that Daniel Gerbet’s work confirms the previous calculations for n ≤ 6. And that’s especially good because previously only one person, Ian Henderson, had done the n = 6 case. See my previous article for details).
But we need some people to help settle the case n = 7!
Addendum: Greg Egan has confirmed this new solution is real. Ian Henderson has confirmed that it’s new, and he’s found the bug in his program that made him overlook it:
It is real! I made a mistaken assumption in my code to try to save computation time — instead of trying every way of orienting the N rectangles, it always orients the last rectangle the same way, under the assumption that the same arrangement but flipped will be generated anyway.
The issue is that “last” is in the order the rectangles are visited, which may change when the square is flipped! (See attached image for the arrangement here—the last rectangle is #6:
Either changing it to always orient the first rectangle in the same way (since it’s always in the top left) or just disabling that code entirely does give a total count of 1372.
Azimuth 
I wonder how many different topologies (modulo symmtries) there are for a given ratio? I didn’t check very much, but at least for 1:3 it is obvious that the solution presented here is not the only possible topology, just imagine 4 rectangles with 1/4,3/4 leaving a square in the middle which can be filled with 3 rectangles with 1/6,1/2.
As the number of rectangles grows, you can get arbitrarily many different topologies modulo symmetries. For example chop the unit square into N vertical strips, each a rectangle of height 1 and width 1/N. Then choose one of these vertical strips and chop it into N squares, each of height 1/N and width 1/N. Then take all of these squares and chop each of them into N vertical strips, each a rectangle of height 1/N and width 1/N2. You can get a lot of different topologies this way.
In fact for any given ratio. If you can tile a square with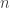
rectangles of that ratio, then you can tile it with 
rectangles of that ratio by replacing one of the rectangles by 4 half size rectangles,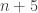 
by replacing on rectangle by one 2/3 size rectangle and 5 1/3 size triangle, 
size rectangle by replacing it by one 
size rectangle and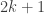 
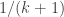size rectangles. Using these in combination one can tile a square with any 
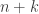rectangles for $\latex k\ge 5$. As there are lots of choices for which rectangles to subdivide, and what combinations of subdivisions to make, it is evident that the number of possible topologies grows faster than any polynomial. I am pretty sure that it grows slower than exponentially, but cannot prove it.
Is the rate of growth of the number of topologies similar for any positive algebraic number all whose conjugates have positive real part? Of course some start later, but do they grow slower?.
In not entirely unrelated news, I had free time because of the snowstorm, so I computed more terms of A359146, getting the sequence 1, 1, 3, 11, 51, 245, 1372, 8522, 58347, 433926. If someone wants, I can generate the pictures, but things seem to be getting beyond human comprehension.
I will soon clean up my sage code so that some other human might understand it and will put it on github.
I also computed the maximum number of different rectangles that can be tiled with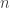
subrectangles having aspect ratios of 
and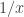 
and got 1, 3, 10, 38, 164, 787, 4258, 25767, 172504, 1258949. The corresponding sequence for guillotine dissections is [A338781](https://oeis.org/A338781}.
One question I have (that I may have the answer to, but haven’t looked closely at the data) is: Does there exist a rational ratio such that the smallest number of rectangles of that ratio that tile the square only tile it in a way that all the rectangles do not have the same orientation.
Wow, I’m impressed that you got that far computing the sequence A359146. I hope that after you put your code on github you can add the new terms in the sequence to the OEIS and include a link to that github. If you don’t know how (I don’t), I can just send the information to Neil Sloane.
Sorry, I don’t know—and right this minute, I should definitely not be thinking about that! Life intrudes. When I get more time the first thing I should think about is the math of guillotine partitions, which is very interesting and somewhat deep. But thanks so much for making this excellent progress. When you get your data onto github, please let me know here.
here is a jupyter/sage notebook that I used to compute the number of partitions.
I will certainly add the results to OEIS once they have stewed for a while, and hopefully at least some of them have been independently verified. As has been amply demonstrated, these are tricky waters, and the OEIS editors are busy enough without having to deal with changing sequences.
Best of luck with life’s intrusions.
Incredible how it’s possible to find new territory in such seemingly simple spaces. Math truly is endlessly fascinating!
Much to my “out of the loop” shock and surprise, just the other day, I chanced to come upon a NY Times article entitled “The Quest to Find Rectangles in a Square (A Puzzle in an online community unlocked a wormhole within the basic shape.)”.
It was in fact that very artricle that led me here to this page and to join in on the discussion.
Believe it or not, and for the record, back in 2017, in connection with my independent investigations into similarity tilings of squares, I’d taken up working on this very problem; and, after a couple of months of painstaking, on and off again efforts,
I’d actually succeeded in working out by hand the case solutions, as well as the polynomials and their evaluations, for n = 4 (11 solutions) and n = 5 (51 solutions).
I meticulously recorded each of these solutions as rough sketches, along with the accompanying polynomials and their associated evaluations, on separate 3X5 index cards and filed them away for safe keeping, thinking that some time in the future I would pursue the matter further and possibly publish and share my findings; but, alas, it appears that I waited just a bit too long.
My only consolation (if that’s what it can properly be called) is that I know in my heart that, oddly enough, the idea to pursue this most intriguing and delightful geometric tiling matter in earnest had evidently occurred to me before it had occurred to anyone else.
I’d be happy to post photos of my 2017 prepared Index Card solutions for n = 4 and n = 5 cases, if anyone is interested in seeing them.