It came as a bit of a shock last week when I realized that some of the equations I’d learned in thermodynamics were just the same as equations I’d learned in classical mechanics—with only the names of the variables changed, to protect the innocent.
Why didn’t anyone tell me?
For example: everybody loves Hamilton’s equations: there are just two, and they summarize the entire essence of classical mechanics. Most people hate the Maxwell relations in thermodynamics: there are lots, and they’re hard to remember.
But what I’d like to show you now is that Hamilton’s equations are Maxwell relations! They’re a special case, and you can derive them the same way. I hope this will make you like the Maxwell relations more, instead of liking Hamilton’s equations less.
First, let’s see what these equations look like. Then let’s see why Hamilton’s equations are a special case of the Maxwell relations. And then let’s talk about how this might help us unify different aspects of physics.
Hamilton’s equations
Suppose you have a particle on the line whose position and momentum
are functions of time,
If the energy
is a function of position and momentum, Hamilton’s equations say:
Maxwell’s relations
There are lots of Maxwell relations, and that’s one reason people hate them. But let’s just talk about two; most of the others work the same way.
Suppose you have a physical system like a box of gas that has some volume pressure
temperature
and entropy
Then the first and second Maxwell relations say:
Comparison
Clearly Hamilton’s equations resemble the Maxwell relations. Please check for yourself that the patterns of variables are exactly the same: only the names have been changed! So, apart from a key subtlety, Hamilton’s equations become the first and second Maxwell relations if we make these replacements:
What’s the key subtlety? One reason people hate the Maxwell’s relations is they have lots of little symbols like saying what to hold constant when we take our partial derivatives. Hamilton’s equations don’t have those.
So, you probably won’t like this, but let’s see what we get if we write Hamilton’s equations so they exactly match the pattern of the Maxwell relations:
This looks a bit weird, and it set me back a day. What does it mean to take the partial derivative of in the
direction while holding
constant, for example?
I still think it’s weird. But I think it’s correct. To see this, let’s derive the Maxwell relations, and then derive Hamilton’s equations using the exact same reasoning, with only the names of variables changed.
Deriving the Maxwell relations
The Maxwell relations are extremely general, so let’s derive them in a way that makes that painfully clear. Suppose we have any smooth function on the plane. Just for laughs, let’s call the coordinates of this plane
and
. Then we have
for some functions and
This equation is just a concise way of saying that
and
The minus sign here is unimportant: you can think of it as a whimsical joke. All the math would work just as well if we left it out.
(In reality, physicists call as the internal energy of a system, regarded as a function of its entropy
and volume
They then call
the temperature and
the pressure. It just so happens that for lots of systems, their internal energy goes down as you increase their volume, so
works out to be positive if we stick in this minus sign, so that’s what people did. But you don’t need to know any of this physics to follow the derivation of the Maxwell relations!)
Now, mixed partial derivatives commute, so we have:
Plugging in our definitions of and
this says
And that’s the first Maxwell relation! So, there’s nothing to it: it’s just a sneaky way of saying that the mixed partial derivatives of the function commute.
The second Maxwell relation works the same way. But seeing this takes a bit of thought, since we need to cook up a suitable function whose mixed partial derivatives are the two sides of this equation:
There are different ways to do this, but for now let me use the time-honored method of ‘pulling the rabbit from the hat’.

Here’s the function we want:
(In thermodynamics this function is called the Helmholtz free energy. It’s sometimes denoted but the International Union of Pure and Applied Chemistry recommends calling it
which stands for the German word ‘Arbeit’, meaning ‘work’.)
Let’s check that this function does the trick:
If we restrict ourselves to any subset of the plane where and
serve as coordinates, the above equation is just a concise way of saying
and
Then since mixed partial derivatives commute, we get:
or in other words:
which is the second Maxwell relation.
We can keep playing this game using various pairs of the four functions as coordinates, and get more Maxwell relations: enough to give ourselves a headache! But we have more better things to do today.
Hamilton’s equations as Maxwell relations
For example: let’s see how Hamilton’s equations fit into this game. Suppose we have a particle on the line. Consider smooth paths where it starts at some fixed position at some fixed time and ends at the point at the time
Nature will choose a path with least action—or at least one that’s a stationary point of the action. Let’s assume there’s a unique such path, and that it depends smoothly on
and
. For this to be true, we may need to restrict
and
to a subset of the plane, but that’s okay: go ahead and pick such a subset.
Given and
in this set, nature will pick the path that’s a stationary point of action; the action of this path is called Hamilton’s principal function and denoted
(Beware: this
is not the same as entropy!)
Let’s assume is smooth. Then we can copy our derivation of the Maxwell equations line for line and get Hamilton’s equations! Let’s do it, skipping some steps but writing down the key results.
For starters we have
for some functions and
called the momentum and energy, which obey
and
As far as I can tell it’s just a cute coincidence that we see a minus sign in the same place as before! Anyway, the fact that mixed partials commute gives us
which is the first of Hamilton’s equations. And now we see that all the funny and
things are actually correct!
Next, we pull a rabbit out of our hat. We define this function:
and check that
This function probably has a standard name, but I don’t know it. Do you?
Then, considering any subset of the plane where and
serve as coordinates, we see that because mixed partials commute:
we get
So, we’re done!
But you might be wondering how we pulled this rabbit out of the hat. More precisely, why did we suspect it was there in the first place? There’s a nice answer if you’re comfortable with differential forms. We start with what we know:
Next, we use this fundamental equation:
to note that:
See? We’ve managed to switch the roles of and
at the cost of an extra minus sign!
Then, if we restrict attention to any contractible open subset of the plane, the Poincaré Lemma says
Since
it follows that there’s a function with
This is our rabbit. And if you ponder the difference between and
, you’ll see it’s
So, it’s no surprise that
The big picture
Now let’s step back and think about what’s going on.
Lately I’ve been trying to unify a bunch of ‘extremal principles’, including:
1) the principle of least action
2) the principle of least energy
3) the principle of maximum entropy
4) the principle of maximum simplicity, or Occam’s razor
In my post on quantropy I explained how the first three principles fit into a single framework if we treat Planck’s constant as an imaginary temperature. The guiding principle of this framework is
subject to the constraints imposed by what you believe
And that’s nice, because E. T. Jaynes has made a powerful case for this principle.
However, when the temperature is imaginary, entropy is so different that it may deserves a new name: say, ‘quantropy’. In particular, it’s complex-valued, so instead of maximizing it we have to look for stationary points: places where its first derivative is zero. But this isn’t so bad. Indeed, a lot of minimum and maximum principles are really ‘stationary principles’ if you examine them carefully.
What about the fourth principle: Occam’s razor? We can formalize this using algorithmic probability theory. Occam’s razor then becomes yet another special case of
subject the constraints imposed by what you believe
once we realize that algorithmic entropy is a special case of ordinary entropy.
All of this deserves plenty of further thought and discussion—but not today!
Today I just want to point out that once we’ve formally unified classical mechanics and thermal statics (often misleadingly called ‘thermodynamics’), as sketched in the article on quantropy, we should be able to take any idea from one subject and transpose it to the other. And it’s true. I just showed you an example, but there are lots of others!
I guessed this should be possible after pondering three famous facts:
• In classical mechanics, if we fix the initial position of a particle, we can pick any position and time
at which the particle’s path ends, and nature will seek the path to this endpoint that minimizes the action. This minimal action is Hamilton’s principal function
which obeys
In thermodynamics, if we fix the entropy and volume
of a box of gas, nature will seek the probability distribution of microstates the minimizes the energy. This minimal energy is the internal energy
, which obeys
• In classical mechanics we have canonically conjugate quantities, while in statistical mechanics we have conjugate variables. In classical mechanics the canonical conjugate of the position is the momentum
, while the canonical conjugate of time
is energy
In thermodynamics, the conjugate of entropy
is temperature
while the conjugate of volume
is pressure
All this is fits in perfectly with the analogy we’ve been using today:
• Something called the Legendre transformation plays a big role both in classical mechanics and thermodynamics. This transformation takes a function of some variable and turns it into a function of the conjugate variable. In our proof of the Maxwell relations, we secretly used a Legendre transformation to pass from the internal energy to the Helmholtz free energy
where we must solve for the entropy in terms of
and
to think of
as a function of these two variables.
Similarly, in our proof of Hamilton’s equations, we passed from Hamilton’s principal function to the function
where we must solve for the position in terms of
and
to think of
as a function of these two variables.
I hope you see that all this stuff fits together in a nice picture, and I hope to say a bit more about it soon. The most exciting thing for me will be to see how symplectic geometry, so important in classical mechanics, can be carried over to thermodynamics. Why? Because I’ve never seen anyone use symplectic geometry in thermodynamics. But maybe I just haven’t looked hard enough!
Indeed, it’s perfectly possible that some people already know what I’ve been saying today. Have you seen someone point out that Hamilton’s equations are a special case of the Maxwell relations? This would seem to be the first step towards importing all of symplectic geometry to thermodynamics.
• Part 1: Hamilton’s equations versus the Maxwell relations.
• Part 2: the role of symplectic geometry.
• Part 3: a detailed analogy between classical mechanics and thermodynamics.
• Part 4: what is the analogue of quantization for thermodynamics?

A couple of tangential remarks
(1) iirc the equations you here advertise as Maxwell’s I was taught as Boltzmann’s?
(2) pardon my French, but an imo good enough reason not to name thermodynamics thermostatics is that in French that name allows to stage the second law with a pun – thus reminding that entropy is a measure of e.g. punning micro-states. L’entropie met un terme aux dynamiques – entropy terminates the dynamics.
Perhaps this:
http://ajp.aapt.org/resource/1/ajpias/v47/i6/p488_s1?isAuthorized=no
is what you’re looking for?
Thanks! I haven’t read the paper yet, but judging from the abstract, it sounds like this guy gets it:
• Mark A. Peterson, Analogy between thermodynamics and mechanics, American Journal of Physics 47 (1979).
I’m surprised this paper isn’t better known! I wonder if it could be because the American Journal of Physics is a ‘teaching journal’.
By the way: I didn’t use the phrase ‘Hamilton–Jacobi’ in my blog article, because I wanted to keep the jargon down to a bare minimum, but of course the idea of deriving Hamilton’s equations by taking derivatives of Hamilton’s principal function is tightly connected to the Hamilton–Jacobi equation. It seems that for the isomorphism between classical mechanics and thermodynamics to become vivid, the Hamilton–Jacobi approach to Hamilton’s equations is nicer than the more common one focused on the phase space with coordinates and
and  . But once we know the isomorphism exists, we can use any approach we want!
. But once we know the isomorphism exists, we can use any approach we want!
Like Blake Stacey says a couple of comments down, any previous work on this correspondence probably stems from Caratheodory’s formulation of thermodynamics, which relies on differential forms… Incidentally, isn’t there a Hamiltonian formulation of geometrical optics? It’d be lovely to get optics into the mix too!
I was wondering why you didn’t mention the Hamilton-Jacobi equation, but now that I’ve had a chance to compare my notes with this blog entry, I agree that your approach is much neater!
The reference I have on Caratheodory’s formulation of thermodynamics is Frankel’s The Geometry of Physics (second edition, 2004), section 6.3, which I’ve never actually read (well, never that carefully). Historical background can be found at a slightly more elementary mathematical level in Max Born’s Natural Philosophy Of Cause And Chance (1949), chapter 5.
I don’t remember what it says about Caratheodory’s formulation of thermodynamics in section 6.3, but that is an awesome book, so you should read it!
There is also a nice connection to optimal control, which relies on a slightly more general definition of an Hamiltonian, based on the Hamilton-Jacobi-Bellman equation.
You can also have a look at this for an historical perspective on the whole thing.
In the discussion on Hamiltonian mechanics, the function X looks like a generating function of the second kind, while S is a generating function of the first kind. Not sure what X is routinely called, though…
Thanks! I didn’t know about the four types of generating functions.
You’re reawakening all those quarter glimpsed things I never fully got:
Why did it also play a role in information geometry?
Given
then where should we expect the Laplace transform to be used? Why Fourier analysis and QM, if that is like the Laplace transform for the imaginary axis?
David Corfield wrote:
I guess we need to understand the essence of the Legendre transform. The Legendre transform shows up whenever we minimize or maximize something subject to constraints. That happens a lot.
Here’s how it goes. Suppose you have a function of two variables—it could be more or fewer, but two is a nice example. Purely for fun let’s call this function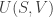 . Now suppose you want to find the minimum of
. Now suppose you want to find the minimum of  subject to a constraint on one of the variables—say,
subject to a constraint on one of the variables—say,  . We can do this using the yoga of Lagrange multipliers, which I hope you know and love. But let me describe that yoga in a mildly nonstandard way.
. We can do this using the yoga of Lagrange multipliers, which I hope you know and love. But let me describe that yoga in a mildly nonstandard way.
First, we find the value of and
and  that minimize
that minimize
Here is called the Lagrange multiplier. We don’t vary it while doing the minimization. Thus, the location of the minimum
is called the Lagrange multiplier. We don’t vary it while doing the minimization. Thus, the location of the minimum 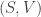 will depend on
will depend on  We figure out how. We then cleverly choose
We figure out how. We then cleverly choose  so that
so that  takes the value given by our constraint. We then read off
takes the value given by our constraint. We then read off 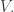
But after we get in the habit of this, we start to love
and think of it in various new ways. It’s a function of three variables. But we can think of it as a function of just and
and  —at least if we’re lucky. How? Because if we fix
—at least if we’re lucky. How? Because if we fix  and
and  , there will be a unique $S$ minimizing
, there will be a unique $S$ minimizing  —at least if we’re lucky. So, we use that
—at least if we’re lucky. So, we use that  . Then
. Then  depends on just
depends on just  and
and 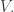
This is what we mean when we write
We call the Legendre transform of our original function
the Legendre transform of our original function  .
.
Now we can approach our original task—locating the minimum of for a fixed value of
for a fixed value of  —in a slightly new way! Now we’re locating the minimum of
—in a slightly new way! Now we’re locating the minimum of  for some fixed value of
for some fixed value of  .
.
It’s all so tautologous and simple that it sounds a bit confusing and pointless. We’re really not doing much! But it sounds grand—in fact it is grand—when we attach physically significant names to our variables.
Our original task was to find what a box of gas will do when it minimizes energy subject to a constraint on entropy.
We’ve changed this to an equivalent problem: find what a box of gas will do when it minimizes free energy subject to a constraint on temperature.
Here ‘find what it would do’ means find the value of the remaining variable , which was a bystander in the above game. But there could be lots of such variables.
, which was a bystander in the above game. But there could be lots of such variables.
Anyway, I hope you get it. We’ve switched our focus from the originally constrained variable to the Lagrange multiplier. We call the Lagrange multiplier the conjugate of the original variable. And we call our new function of interest (here ) the Legendre transform of our original function (here
) the Legendre transform of our original function (here  ).
).
I gave my current favorite explanation of the ‘essence’ of the Legendre transformation, but I didn’t answer David’s real puzzle, which I take to be: if the Legendre transformation can be seen as as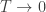 limit of the Laplace transform, why do we see both Laplace transforms and Legendre transformations showing up in
limit of the Laplace transform, why do we see both Laplace transforms and Legendre transformations showing up in  thermal statics?
thermal statics?
This is a great puzzle and I don’t think I’ve reached the bottom of it. But here’s a start.
In the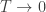 limit of thermal statics, it reduces to classical statics, where the principle of least energy reigns supreme. Whenever we minimize things we expect to see Legendre transformations, so in classical statics we do.
limit of thermal statics, it reduces to classical statics, where the principle of least energy reigns supreme. Whenever we minimize things we expect to see Legendre transformations, so in classical statics we do.
As we go to we’re doing thermal statics. Now, instead of choosing the one state of minimum energy we say all possible states occur with different probabilities—with a state of energy
we’re doing thermal statics. Now, instead of choosing the one state of minimum energy we say all possible states occur with different probabilities—with a state of energy  showing up with probability proportional to
showing up with probability proportional to  . So, our Legendre transforms turn into Laplace transforms.
. So, our Legendre transforms turn into Laplace transforms.
But, this probability distribution on states still minimizes something: namely, the free energy! So, we still see Legendre transforms showing up in thermal statics!
So, we see both Laplace transforms and Legendre transforms in thermal statics.
Ah, that makes sense. Something similar happens with probabilities (though in view of the association between energies and probabilities that was always likely). When you have a distribution over a space you can always lift it up to a point in the space of distributions. So the Legendre distribution in the latter case is shifting you between coordinates for the moment-determined subspaces and those of the corresponding exponential families.
I’d guess that any prior work in this spirit would derive from the Caratheordory tradition of thermodynamics (which originally got started by a suggestion from Max Born).
Here’s M. J. Peterson (1979), “Analogy between thermodynamics and mechanics” American Journal of Physics 47, 6: 488, DOI:10.1119/1.11788.
Here’s what Peterson says in his introduction:
The basic Poisson brackets he uses are
and
Yes, these Poisson brackets are just what you’d expect from the relation I gave:
In fact I wrote it this way to hint at the canonically conjugate pairs (or if you prefer, thermodynamically conjugate variables). I have a blog article half-written about this symplectic stuff.
Well, actually his Poisson brackets differ by an overall sign from the usual ones in classical mechanics, if you use the analogy I suggest. But that’s not surprising: the overall sign of the Poisson brackets is somewhat a matter of convention (though the conventions interlock and you have to be careful of changing just one).
John:
I am currently teaching a thermodynamics class, and really enjoying your series of posts starting quantropy. I will seriously look into them once I have some free time.
Best,
Demian
Oh. I forgot to mention.
I have a sophomore with whom we decide to go through Baez and Muniain this semester. Let’s see how far we can make to.
Demian
Hi, Demian! You wrote:
Great! As Mark Peterson points out in his paper, the analogy between classical mechanics and thermodynamics makes a lot of things clearer. It would be fun to incorporate that into a course, and from the comments here you’ll see a number of people are already doing it. I’d love to try it myself someday—maybe when I get back to U.C. Riverside.
For some time I’ve suspected that various physical theories somehow use the same mathematics, but don’t have sufficient background to test this out. Your example here would be one of them. A friend of mine, Rob Tyler, once told me that he had published an article somewhere showing that the equations of electromagnetism are the same as those of fluid dynamics (Maxwell’s equations correspond to the vorticity relations I think). I’m not sure where all this leads, but at least it suggested a cute possibility on that score: what if anyone who solved either Yang-Mills or Navier-Stokes was entitled to $2,000,000 from the Clay foundation since by solving one they’d essentially solved the other? I just wish I knew what I was talking about on the matter.
A symplectric structure of thermodynamics? Cool beans.
Qualitatively, I don’t see that as very surprising. It has been known for a long time by mathematicians that symplectic topology has very deep and rich applications in quantum mechanics. Also, as several of your former posts indicate, quantum mechanics itself shares many similarities with thermodynamics (this is especially true if you subscribe to the ensemble interpretation).
It is important to look a bit deeper into the physics behind the equations, though. Hamiltonian mechanics goes far beyond just Hamilton’s equations of motion. The richness of Hamiltonian questions raises a few questions about this article: What does the fact that being invariant with varying
being invariant with varying  signify physically (analogous to the Poincare/Liouville integral invarint)? Can you relate thermodynamic variable via canonical transformations? Is the symplectic theory of thermodynamics useful in applications or in theory (perhaps symplectic integration of thermodynamic quantities could prove useful for engineers)?
signify physically (analogous to the Poincare/Liouville integral invarint)? Can you relate thermodynamic variable via canonical transformations? Is the symplectic theory of thermodynamics useful in applications or in theory (perhaps symplectic integration of thermodynamic quantities could prove useful for engineers)?
Darn, it is curiosities like these that make me regret my ignorance of thermodynamics!
One of the first things I learned to do with Hamilton’s equations of motion was to study the case where the initial condition is not exactly known: instead of saying we have at time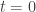 a particle at
a particle at  with momentum
with momentum  , or a set of particles with a well-specified position and momentum each, all we know is the probability density for where things are and what they’re doing,
, or a set of particles with a well-specified position and momentum each, all we know is the probability density for where things are and what they’re doing,  . If this is how we’ll gamble about what’s happening at time
. If this is how we’ll gamble about what’s happening at time  , and if we accept that Newton’s laws apply, how should we gamble about what will happen at
, and if we accept that Newton’s laws apply, how should we gamble about what will happen at  ? The Liouville equation tells us
? The Liouville equation tells us
where is the Hamiltonian which encodes all the ways the
is the Hamiltonian which encodes all the ways the  particles can push and pull on one another.
particles can push and pull on one another.
So, by formal analogy, can we say something about “statistical thermal statics”, i.e., a situation where we don’t know exact values for the macroscopic state variables? I guess the formal analogue of the Liouville equation would read
relating the change in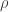 under an infinitesimal quasi-static change in volume
under an infinitesimal quasi-static change in volume  to the Poisson bracket of
to the Poisson bracket of 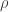 with the pressure
with the pressure  .
.
Blake wrote:
That’s an interesting idea! It’s sort of amusing, since in statistical mechanics, thermal statics is already statistical. But taking a probability distributions of probability distribution, and collapsing it down to a probability distribution, is a perfectly fine thing (formalized using the Giry monad, if you feel like showing off).
I think you’re exactly right about the analogue of the Liouville equation (though I don’t vouch for the minus sign); this should be a spinoff of M. J. Peterson’s comment:
Is a probability distribution of probability distributions the same thing as Christian Beck’s superstatistics or a doubly stochastic model?
The interesting thing about this monad is that it can lead to PDF’s that lack defined moments. For example the practice of applying an exponential distribution to an exponential distribution leads to a resultant PDF which lacks a mean but still has a median value. I have a feeling that this is a maximum entropy situation for a median-only constrained PDF, but I haven’t been able to set up the variational parameters correctly.
So my math puzzle is “Find the maximum entropy probability density function given a constraint of known median value”.
John Baez wrote:
Right. On the other hand, a statement like “the temperature is 300 plus-or-minus 5 degrees Celsius” makes sense in an engineering context.
Where can I learn how to show off — starting here, maybe?
Since WebHubTel and Blake are both interested in probability distributions of probability distributions, and the literature I’ve been able to find doesn’t look as readable as it should be, here’s a little mini-course:
Probability distributions aren’t nearly as flexible as probability measures, so we should really use those. Suppose is a space, and let
is a space, and let  be the space of probability measures on
be the space of probability measures on  Then we’d like to talk about
Then we’d like to talk about 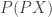 , the space of probability measures on the space of probability measures on
, the space of probability measures on the space of probability measures on  And there should be a map
And there should be a map
which collapses a probability measure on the space of probability measures on down to a probability measure on
down to a probability measure on 
For example, if there’s a 50% chance that the coin in my hand is fair (so it has a 50% chance of landing heads up), but there’s a 50% chance that it’s rigged so that it has a 90% chance of landing heads up, we say there’s a 70% chance of its landing heads up.
It’s not hard write down a formula for how should work in general, so I’ll leave that as a little exercise. The challenging part is this:
should work in general, so I’ll leave that as a little exercise. The challenging part is this:
When I say is ‘a space’ I’m being pretty vague. We need
is ‘a space’ I’m being pretty vague. We need  to be a measurable space to define measures on it. That’s straightforward enough… but then we need
to be a measurable space to define measures on it. That’s straightforward enough… but then we need  to also be a measurable space, so we can define
to also be a measurable space, so we can define 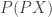 .
.
So, we need to find some class of measurable spaces such that
such that  is again a measurable space. And ideally we’d like
is again a measurable space. And ideally we’d like  to again be a measurable space in the same class! That would let us go hog-wild and define not just
to again be a measurable space in the same class! That would let us go hog-wild and define not just 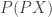 but also
but also  and so on. Believe it or not, these things are useful too!
and so on. Believe it or not, these things are useful too!
Mathematicians have found a nice answer to this puzzle, though perhaps not the ultimate ideal answer: it’s to use ‘standard Borel spaces’. This is a class of measure spaces that includes all the ones you’d ever care about (unless you’re really insane!), and has the property that if is a standard Borel space, so is
is a standard Borel space, so is 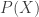 . Even better, there’s a nice complete classification of standard Borel spaces: two standard Borel spaces are isomorphic iff they have the same cardinality. This is a theorem due to Kuratowski.
. Even better, there’s a nice complete classification of standard Borel spaces: two standard Borel spaces are isomorphic iff they have the same cardinality. This is a theorem due to Kuratowski.
So, it turns out we get a functor sending standard Borel spaces to standard Borel spaces, and a monad
sending standard Borel spaces to standard Borel spaces, and a monad  , meaning that for each standard Borel space
, meaning that for each standard Borel space  we get a map
we get a map
as desired, and this map is incredibly well-behaved. Now is not the time for me to explain monads; I’ve done it before in This Week’s Finds. But anyway, this functor is sometimes called the Giry monad… though often people use that term to mean something very slightly different, where instead of probability measures we use measures whose integral is less than or equal to 1 (called sub-probability measures).
is sometimes called the Giry monad… though often people use that term to mean something very slightly different, where instead of probability measures we use measures whose integral is less than or equal to 1 (called sub-probability measures).
So, what’s a standard Borel space? I explained that in week272, but I’ll say it again:
For starters, it’s a kind of measurable space, meaning a space equipped a collection of subsets that’s closed under countable intersections, countable unions and complement. Such a collection is called a sigma-algebra and we call the sets in the collection measurable. A measure on a measurable space assigns a number between 0 and +∞ to each measurable set, in such a way that for any countable disjoint union of measurable sets, the measure of their union is the sum of their measures.
A nice way to build a measurable space is to start with a topological space. Then you take its open sets and keep taking countable intersections, countable unions and complements until you get a sigma-algebra. This may take a long time, but if you believe in transfinite induction you’re bound to eventually succeed. The sets in this sigma-algebra are called Borel sets.
A basic result in real analysis is that if you put the usual topology on the real line, and use this to cook up a sigma-algebra as just described, there’s a unique measure on the resulting measurable space that assigns to each interval its usual length. This is called Lebesgue measure.
Some topological spaces are big and nasty. But separable complete metric spaces are not so bad.
We don’t care about the metric in this game. So, we use the term Polish space for a topological space that’s homeomorphic to a complete separable metric space. It was the Poles, like Kuratowski, who first got into this stuff.
And often we don’t even care about the topology. So, we use the term standard Borel space for a measure space whose measurable sets are the Borel sets for some topology making it into a Polish space.
In short: every complete separable metric space has a Polish space as its underlying topological space, and every Polish space has a standard Borel space as its underlying measurable space.
Now, it’s hopeless to classify complete separable metric spaces. It’s even hopeless to classify Polish spaces. But it’s not hopeless to classify standard Borel spaces! The reason is that metric spaces are like diamonds: you can’t bend or stretch them at all without breaking them entirely. But topological spaces are like rubber… and measurable spaces are like dust. So, it’s very hard for two metric spaces to be isomorphic, but it’s easier for their underlying
topological spaces – and even easier for their underlying measurable spaces.
For example, the line and plane are isomorphic, if we use their usual sigma-algebras of Borel sets to make them into measurable spaces! And the plane is isomorphic to for every
for every  , and all these are isomorphic to a separable Hilbert space! As measurable spaces, that is.
, and all these are isomorphic to a separable Hilbert space! As measurable spaces, that is.
In fact, every standard Borel space is isomorphic to one of these:
• a countable set with its sigma-algebra of all subsets,
• the real line with its sigma-algebra of Borel subsets.
That’s pretty amazing. It means that standard Borel spaces are classified by just their cardinality, which can only be finite, countably infinite, or the cardinality of the continuum. The "continuum hypothesis" says there’s no cardinality between the countably infinite one and the cardinality of the continuum–but we don’t need the continuum hypothesis to prove this result.
Here’s some of the conversation about this blog entry from Google+
Allen Knutson wrote:
Dan Piponi wrote:
Stephen Lavelle wrote:
John Baez wrote:
John Baez wrote:
Jim Walters wrote:
Nathan Reed wrote:
Cliff Harvey wrote:
Kazimierz Kurz wrote:
Dan Piponi wrote:
Ekaropolus Van Gor wrote:
John Baez wrote:
John Baez wrote:
John Baez wrote:
Bernard Beard wrote:
John Baez wrote:
An ongoing discussion of non-equilibrium thermodynamics and maximum entropy at the Climate Etc.blog:
I was trying to defend the concept of maximum entropy but the pushback I keep getting is that it doesn’t produce any new insight that you can’t get though conventional stat mech.
An upcoming topic there is Gell-Mann’s concept of complexity/simplicity referred to as plectics. This is interesting because it may fit into the Occam’s razor bucket of parsimony and is the root term in symplectic geometry.
The climate scientists are interested in this general topic because it could help make headway into complex general circulation models (GCM’s).
V.I. Arnold once wrote something along the lines of: the reason why thermodynamics is hard is that it is naturally formulated on an odd-dimensional phase space. I.e. contact geometry as opposed to symplectic geometry. This makes me a bit suspicious of such a direct analogy between thermodynamics and classical mechanics.
On other hand, quantum statistical mechanics does seem to be relatable to classical mechanics. Since there is always an irrelevant overall complex phase in QM, it is natural to consider the projective Hilbert space. Brody and Hughston showed that the projective Hilbert space is a symplectic manifold. The paper is “Geometrization of statistical mechanics” Proc. R. Soc. Lond. A (1999) 455, 1683–1715
Matt wrote:
Well, I like contact geometry too, and I’d be very interested to see what Arnol’d was actually talking about. What’s the simplest example does he give of an odd-dimensional phase space in thermodynamics?
As you can see from my post, thermodynamics works quite nicely on an even-dimensional phase space. But that doesn’t necessarily conflict with the odd-dimensional approach. Indeed, classical mechanics can be formulated nicely on either an even-dimensional symplectic manifold or an odd-dimensional contact manifold. So, we can use the analogy between classical mechanics and thermodynamics, described here, to cook up an odd-dimensional phase space for thermodynamics. In the example I’m talking about this article, I think that would have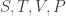 and
and  as coordinates.
as coordinates.
Here’s another nice paper emphasizing the fact that a projectivized Hilbert space is a symplectic manifold:
• Abhay Ashtekar and Troy Schiling, Geometrical formulation of quantum mechanics.
Above we see Dan Piponi wondering about the Legendre transform in classical statics versus the Laplace transform in thermal statics, and me responding that the former is a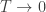 limit of the latter. If we formally make the temperature
limit of the latter. If we formally make the temperature  imaginary we get quantum mechanics and the Fourier transform.
imaginary we get quantum mechanics and the Fourier transform.
Dan has now explained some of these ideas in detail here:
• Dan Piponi, Some parallels between classical and quantum mechanics, A Neighborhood of Infinity, 21 January 2012.
He concludes as follows:
It’s really in thermal statics that we can rigorously understand how the semiring arises from a 1-parameter deformation of the semiring
arises from a 1-parameter deformation of the semiring 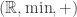 . The parameter is temperature,
. The parameter is temperature,  . A further ‘Wick rotation’ gives us quantum mechanics with
. A further ‘Wick rotation’ gives us quantum mechanics with
I’m not sure these free online books exactly what Dan wants, but it’s probably buried in them somewhere:
• Grigory L. Litvinov, Victor Maslov, and Sergei Sergeev, Idempotent and tropical mathematics and problems of mathematical physics (Volume I).
• Grigory L. Litvinov, Victor Maslov, and Sergei Sergeev, Idempotent and tropical mathematics and problems of mathematical physics (Volume II).
These were the proceedings of the International Workshop on Idempotent and Tropical Mathematics and Problems of Mathematical Physics, held at the Independent University of Moscow, Russia in 2007. Litvinov has also written other good review articles, like this:
• Grigory L. Litvinov, The Maslov dequantization, idempotent and tropical mathematics: A brief introduction.
It’s good to look for papers containing the buzzword ‘idempotent analysis’. This comes from the fact that addition in the semiring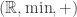 . is idempotent:
. is idempotent:
Thank you John for the link to Ashtekar and Schilling’s work. This a much more complete statement of what I was trying to say.
As for the Arnol’d quote…it was from memory and I slightly embellished it, but it can be found in his contribution to the Gibbs Symposium in 1989:
http://books.google.com/books?id=0ZwmLz_UTYoC&pg=PA163&dq=gibbs+symposium+%2Barnold&hl=en#v=onepage&q=gibbs%20symposium%20%2Barnold&f=false
My understanding has always been that in thermodynamics the macroscopic quantities come in pairs — one extensive and one intensive — with one singleton extensive quantity left over. For example the pairs are typically taken to be (energy, temperature), (volume, pressure), (particle number, chemical potential), etc. In this description, entropy is the odd one out and the goal of thermodynamics is to write down .
.
(It is tempting to imagine that time is conjugate to
is conjugate to  — second law any one?! — but as you point out we are really doing thermostatics not thermodynamics!)
— second law any one?! — but as you point out we are really doing thermostatics not thermodynamics!)
So I guess I don’t see that odd-dimensional phase spaces need to be cooked up. On the other hand, I never knew that classical mechanics could be formulated on contact manifolds as well!
V.I. Arnold has certainly discussed many of these topics. For example in the reference given by Matt Parry, as well as in “Symplectic geometry and its applications” here: http://books.google.co.nz/books/about/Dynamical_systems.html?id=roMpAQAAMAAJ&redir_esc=y (discusses symplectic geometry, contact geometry, classical mechanics, thermodynamics, quantum mehanics etc) and a number of other sources.
I took a course at UIUC that taught thermodynamics using differential forms. The course covered various applications of differential forms/differential geometry and thermodynamics was just one of many. I lost my notes and don’t remember the visiting professor’s name, but I remember how excited he was. The presentation was similar to what you have here.
I’ve seen lots of presentations of thermodynamics using differential forms. I’d never seen the analogy to classical mechanics exploited to bring symplectic geometry (or if you like, Poisson brackets) into play in thermodynamics. But you can find it in Peterson’s paper, and also maybe Jamiołkowski, Ingarden, and Mrugała’s book Fizyka Statystyczna i Termodynamika.
Did your professor talk about Poisson brackets in thermodynamics? I’m curious how well-known these are.
Yes. I believe he did, but it was long ago and this stuff was pretty new to me back then. The visiting professor was Eastern European (I believe) and I wouldn’t be surprised if his reference was the latter one you mention.
I showed you last time that in many branches of physics—including classical mechanics and thermodynamics—we can see our task as minimizing or maximizing some function. Today I want to show how we get from that task to symplectic geometry.
Maybe this could be interesting: http://www.amazon.de/Theoretische-Physik-Statistische-Theorie-Springer-Lehrbuch/dp/3540798234
I don’t know if there is an english translation..
Hello Azimuth, I love your article on the deep connections between Hamilton’s equations of classical mechanics and the Maxwell relations of thermodynamics!! Is this in a book somewhere? (I don’t have a printer.) Best regards, Michael Martin, MD. (Just an MD, not a PhD!)
Not that I know of–this is stuff I’m making up as I go along. Probably someone knows it, but if I’d seen it somewhere I probably wouldn’t be talking about it.
this is an interesting post—i saw it months ago. i collect papers more or less showing equivalences between classical mechanics and thermodynamics/ nonequilibrium stat mech. ( i hadnt even considered maxwells electrodynamics, except that there appear to be at least two lagrangians that will get you there).
there is the well known attempt via fisher information (reviewed critically by streater) and many other more current ones (some just qualitative—eg i noticed the ‘gravity law’ in economics was derived via stat mech by a wilson in the 60’s).
i guess i first saw this type of thing in the onsager-machlup functional—you can get a principle of least action/hamilton jacobi eqn for diffusion (ie a conservative process for what is usually thought of as a nonconservative one).
(there is alot of this stuff out there—it even has now gotten into proc royal society london by several authors, who often dont cite each other).
i cant really figure out if all the approaches are the same (one can even go into e nelson’s approach to quantum theory).
(my niece is in high school in singapore as an aside).
I was surprised to rediscover that the Maxwell relations in thermodynamics are formally identical to Hamilton’s equations in classical mechanics—though in retrospect it’s obvious. Thermodynamics obeys the principle of maximum entropy, while classical mechanics obeys the principle of least action. Wherever there’s an extremal principle, symplectic geometry, and equations like Hamilton’s equations, are sure to follow.
[…] As always physics rules when it comes to defining natural behavior, and so we start by looking at energy balance. Consider a Gibbs energy formulation as a variational approach: […]
[…] original post on the CSALT model gave a flavor of the variational approach that I used — essentially solving for a thermostatic free energy minimum with respect to the […]
I am not clear on something. The derivations in the post are completely general, but also completely formal.
It seem that any sufficiently smooth relation
can be expressed as
with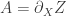 and
and  , giving
, giving  Defining
Defining 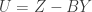 then also gives
then also gives
This is all independent of the fact that and
and  are both energy.
are both energy.
No conservation laws or variational principles are used in the derivations. What is the significance of the connection between CM and TM?
Variational principles are implicit in what I’m doing, even though they’re not required for the calculations you wrote down. All the mathematical structures in this post—and even more, as described in Part 2—show up whenever we try to extremize a smooth function of several variables. In classical mechanics we’re minimizing Hamilton’s principal function (basically the action); in thermodynamics we’re minimizing entropy.
Given this, the interesting puzzle—to me, anyway—is the relation between the principle of least action and the principle of maximum entropy. That’s what Blake Pollard and I investigated in our paper on quantropy. There’s still more to understand, though!
Given that the integral of Hamilton’s principal function over a path seems only to depend on the difference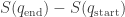 , what is the result of ‘minimising S’? It surely can’t be a path. Or perhaps I’m missing something crucial about how to integrate
, what is the result of ‘minimising S’? It surely can’t be a path. Or perhaps I’m missing something crucial about how to integrate  ?
?
ejlflop wrote:
I’m confused. Hamilton’s principal function is itself defined as an integral over a path; it’s not something we typically integrate over a path.
Sorry, I meant integrating .
.
I think what I don’t understand is what role the HPF plays in this recipe for mechanics. Is it: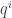 represents time, label
represents time, label 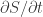 as
as 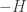 , and hence derive Hamilton’s equations
, and hence derive Hamilton’s equations
1. Use some minimisation procedure to find path
2. Evaluate HPF for that path
3. Decide which
?
In which case I think I was looking for step 1 somewhere in your post, and getting confused.
Incidentally, I find methods like this that put time and space coordinates on an equal footing to be very attractive — as far as I’m concerned, they only differ because they show up in different places in a Lorentzian metric. However, looking it up it seems that this is called ‘non-autonomous mechanics’ and is in general fairly tricky, e.g. I found http://arxiv.org/pdf/math-ph/0604063.pdf
(Though the text you posted http://math.ucr.edu/home/baez/toby/Hamiltonian.pdf also seems to apply to this case, though it seems to assume you’ve already picked a hypersurface, and doesn’t contain any details of a minimisation procedure)
Yes, that’s about right.
I explained it here:
Of course this is just a special case of a more general procedure. For example we could consider a spacetime manifold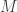 and fix a point
and fix a point 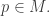
Suppose we can define a quantity called the ‘action’ for any path![\gamma : [0,1] \to M](https://s0.wp.com/latex.php?latex=%5Cgamma+%3A+%5B0%2C1%5D+%5Cto+M&bg=ffffff&fg=333333&s=0&c=20201002) . Suppose there is a unique action-minimizing path from
. Suppose there is a unique action-minimizing path from  to any point
to any point  . Then given
. Then given  , let
, let  be the action of the action-minimizing path from
be the action of the action-minimizing path from 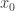 to the point
to the point  Then
Then
is Hamilton’s principal function, and starting from here we can derive Hamilton’s equations as explained in my blog article.
We can work in arbitrary coordinates and write the coordinates of as
as  We don’t need to choose one coordinate and call it ‘time’: the formalism doesn’t really require that. Hamilton’s equations are really just the trivial statement that
We don’t need to choose one coordinate and call it ‘time’: the formalism doesn’t really require that. Hamilton’s equations are really just the trivial statement that
Here I’m assuming that everything is as differentiable as we want it to be, and just to be careful I’m assuming there’s a unique action-minimizing path. The second assumption is false when there are ‘caustics’.
Ah, I think I’ve got it! Thanks a lot.
I suppose the awkward bit would be finding an expression for the action that is also agnostic with respect to the choice of time coordinate. A physical theory with action does seem to give a special role to
does seem to give a special role to  , while it’s much more elegant to parametrise
, while it’s much more elegant to parametrise  by arc length as you did and never have to mention time at all.
by arc length as you did and never have to mention time at all.
I wonder if it would turn into a field theory at that point, though.
In all relativistic theories of classical point particles you can write the action as
where is an arbitrary parameter, not necessarily arclength. (Indeed, for particles moving at the speed of light the arclength is zero, so it’s no good as a parameter!)
is an arbitrary parameter, not necessarily arclength. (Indeed, for particles moving at the speed of light the arclength is zero, so it’s no good as a parameter!)
You can see this done e.g. starting in Section 3.5.2 of this book:
• John Baez, Blair Smith and Derek Wise, Lectures on Classical Mechanics.
It’s just a draft but it’s fairly readable.
What is the philosophy behind the general idea: (quantity) = (conjugate1) – (conjugate2), e.g., the Lagrangian dS = Tdt -Vdt.
Roy Frieden has introduced the Extreme physical information principle, but it’s a controversial idea. https://en.wikipedia.org/wiki/Extreme_physical_information
Herb— R F Streater in his 2007 book ‘lost causes in and beyond physics’ (see amazon) discusses and dismisses frieden’s papers (physics from fisher information).
I happen to think Frieden was on to something, and he kept publishing ( Streater was top notch but he may have got that wrong. Even Oppenheimer said Feynman didnt make any sense.)
. The same issue applies in population genetics ( is ‘fisher’s fundamental theorem of natural selection’ a ‘maximum entropy principle’ or a newtonian ‘potential energy minimization’ problem? elliot sober (philosopher of of science at U Wisconsin) among others have numerous papers on this.
The same issue occurs in General equilibrium theory in economics (Arrow-Hahn-Debreu-Mantel-Sonnenschein) . Do markets maximize entropy or minimize potential energy to achieve ‘pareto optimality’?
My impression is you can do it both ways. (see the book by ingrao and israel ‘economic equilibirium in the history of science’).
More recent papers derive general relativity from a max ent principle.
btw is there a way for me to fix my own mess or a get a preview.
Sorry, no preview available here. The bug in your post was a subtle one (after you fixed the obvious ones). I fixed the problem by retyping the letters in your LaTeX comments that didn’t parse. Sometimes this happens when people cut-and-paste text that’s in a strange font.
A formalism for contact geometry and relation to thermodynamics:
• A. Bravetti, C. S. Lopez-Monsalvo and F. Nettel, Contact symmetries and Hamiltonian thermodynamics.
Thanks! It’s interesting how they seem to be claiming to get a metric on their contact manifold using the Fisher information metric. At least that’s how I interpret the first sentence of their abstract:
1) We should keep in mind that classical mechanics is only an approximation to quantum mechanics, just as classical thermodynamics is only an approximation to statistical mechanics.
The symplectic structure is even more interesting and more useful when applied to the modern (post-classical) versions. Hamilton-Jacobi theory is amusing, but it’s less useful than out-and-out QM, and not significantly simpler.
2) Stat mech is basically the analytic continuation of QM, continued in the direction of imaginary time. This point and its ramifications are discussed in e.g. Feynman and Hibbs Quantum Mechanics and Path Integrals (1965). The classical limit of QM is obtained by the method of stationary phase, whereas the classical limit of stat mech is obtained by the method of steepest descent … so the two subjects are very nearly but not quite identical.
Again: If we’re going to make connections, it is even more interesting and more useful to connect the modern (post-classical) versions.
FWIW note that Planck invented QM as an outgrowth from stat mech … not directly from classical mechanics. So the connections are there, and have been since Day One.
3) Many (but not all) of the familiar formulas of thermodynamics can usefully be translated to the language of differential forms. In many cases all that is required is a re-interpretation of the symbols, leaving the form of the formula unchanged; for instance we interpret dE = T dS – P dV as a vector equation.
I say “not all” formulas because more than a few of the formulas you see in typical thermodynamics books are nonsense. This includes (almost) all expressions involving “dQ” or “dW”. Such things simply do not exist (except in trivial cases). Daniel Schroeder in An Introduction to Thermal Physics (1999) rightly calls them a crime against the laws of mathematics. With a modicum of self-discipline it is straightforward to do thermodynamics without committing such crimes.
Differential forms make thermodynamics simpler and more visually intuitive … and simultaneously more sophisticated, more powerful, and more correct.
Although there are fat books on the subject of differential topology, only the tiniest fraction of that is necessary for present purposes. An introductory discussion (including pictures) can be found at https://www.av8n.com/physics/thermo-forms.htm and the application to thermodynamics is worked out in some detail at https://www.av8n.com/physics/thermo/.
Is the contrast between having QM derive from stat mech and having it from classical mechanics, not really stiffer or steeper than presented here? If you start from the stat mech side isn’t there a sense by which the other view misleads on the materiality or definiteness of the wave function outside any context of identically prepared systems?
[…] John Baez has an interesting pair of articles on his Azimuth blog about the Maxwell relations: https://johncarlosbaez.wordpress.com/2012/01/19/classical-mechanics-versus-thermodynamics-part-1/ https://johncarlosbaez.wordpress.com/2012/01/23/classical-mechanics-versus-thermodynamics-part-2/ […]
[…] • Classical mechanics versus thermodynamics (part 1). […]
V. I. Arnold wrote: “Symplectic geometry is the mathematical apparatus of such areas of physics as classical mechanics, geometrical optics and thermodynamics. Whenever the equations of a theory can be gotten out of a variational principle, symplectic geometry clears up and systematizes the relations between the quantities entering into the theory. Symplectic geometry simplifies and makes perceptible the frightening formal apparatus of Hamiltonian dynamics and the calculus of variations in the same way that the ordinary geometry of vector spaces reduces cumbersome coordinate computations to a small number of simple basic principles.”
Arnol’d V.I., Givental’ A.B., Novikov S.P. (2001) Symplectic Geometry. In: Arnold V.I., Novikov S.P. (eds) Dynamical Systems IV. Encyclopaedia of Mathematical Sciences, vol 4. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-06791-8_1
[…] and (https://arxiv.org/pdf/0806.1147), the very clear (https://johncarlosbaez.wordpress.com/2012/01/19/classical-mechanics-versus-thermodynamics-part-1/) and, at a higher level […]
I recall reading something similar in
• M. A. Peterson, Analogy between thermodynamics and mechanics, American Journal of Physics 47 (1979), 488-490.
after taking a thermodynamics class based on Callen’s thermodynamics class.
Nice! Thanks!