Classical Mechanics versus Thermodynamics (Part 2)

I showed you last time that in many branches of physics—including classical mechanics and thermodynamics—we can see our task as minimizing or maximizing some function. Today I want to show how we get from that task to symplectic geometry.

So, suppose we have a smooth function

S: Q \to \mathbb{R}

where Q is some manifold. A minimum or maximum of S can only occur at a point where

d S = 0

Here the differential d S which is a 1-form on Q. If we pick local coordinates q^i in some open set of Q, then we have

\displaystyle {d S = \frac{\partial S}{\partial q^i} dq^i }

and these derivatives \displaystyle{ \frac{\partial S}{\partial q^i} } are very interesting. Let’s see why:

Example 1. In classical mechanics, consider a particle on a manifold X. Suppose the particle starts at some fixed position at some fixed time. Suppose that it ends up at the position x at time t. Then the particle will seek to follow a path that minimizes the action given these conditions. Assume this path exists and is unique. The action of this path is then called Hamilton’s principal function, S(x,t). Let

Q = X \times \mathbb{R}

and assume Hamilton’s principal function is a smooth function

S : Q \to \mathbb{R}

We then have

d S = p_i dq^i - H d t

where q^i are local coordinates on X,

\displaystyle{ p_i = \frac{\partial S}{\partial q^i} }

is called the momentum in the ith direction, and

\displaystyle{ H = - \frac{\partial S}{\partial t} }

is called the energy. The minus signs here are basically just a mild nuisance. Time is different from space, and in special relativity the difference comes from a minus sign, but I don’t think that’s the explanation here. We could get rid of the minus signs by working with negative energy, but it’s not such a big deal.

Example 2. In thermodynamics, consider a system with the internal energy U and volume V. Then the system will choose a state that maximizes the entropy given these constraints. Assume this state exists and is unique. Call the entropy of this state S(U,V). Let

Q = \mathbb{R}^2

and assume the entropy is a smooth function

S : Q \to \mathbb{R}

We then have

d S = \displaystyle{\frac{1}{T} d U - \frac{P}{T} d V }

where T is the temperature of the system, and P is the pressure. The slight awkwardness of this formula makes people favor other setups.

Example 3. In thermodynamics there are many setups for studying the same system using different minimum or maximum principles. One of the most popular is called the energy scheme. If internal energy increases with increasing entropy, as usually the case, this scheme is equivalent to the one we just saw.

In the energy scheme we fix the entropy S and volume V. Then the system will choose a state that minimizes the internal energy given these constraints. Assume this state exists and is unique. Call the internal energy of this state U(S,V). Let

Q = \mathbb{R}^2

and assume the entropy is a smooth function

S : Q \to \mathbb{R}

We then have

d U = T d S - P d V

where

\displaystyle{ T = \frac{\partial U}{\partial S} }

is the temperature, and

\displaystyle{ P = - \frac{\partial U}{\partial V} }

is the pressure. You’ll note the formulas here closely resemble those in Example 1!

Example 4. Here are the four most popular schemes for thermodynamics:

• If we fix the entropy S and volume V, the system will choose a state that minimizes the internal energy U(S,V).

• If we fix the entropy S and pressure P, the system will choose a state that minimizes the enthalpy H(S,P).

• If we fix the temperature T and volume V, the system will choose a state that minimizes the Helmholtz free energy A(T,V).

• If we fix the temperature T and pressure P, the system will choose a state that minimizes the Gibbs free energy G(T,P).

These quantities are related by a pack of similar-looking formulas, from which we may derive a mind-numbing little labyrinth of Maxwell relations. But for now, all we need to know is that all these approaches to thermodynamics are equivalent given some reasonable assumptions, and all the formulas and relations can be derived using the Legendre transformation trick I explained last time. So, I won’t repeat what we did in Example 3 for all these other cases!

Example 5. In classical statics, consider a particle on a manifold Q. This particle will seek to minimize its potential energy V(q), which we’ll assume is some smooth function of its position q \in Q. We then have

d V = -F_i dq^i

where q^i are local coordinates on Q and

\displaystyle{ F_i = -\frac{\partial V}{\partial q^i} }

is called the force in the ith direction.

Conjugate variables

So, the partial derivatives of the quantity we’re trying to minimize or maximize are very important! As a result, we often want to give them more of an equal status as independent quantities in their own right. Then we call them ‘conjugate variables’.

To make this precise, consider the cotangent bundle T^* Q, which has local coordinates q^i (coming from the coordinates on Q) and p_i (the corresponding coordinates on each cotangent space). We then call p_i the conjugate variable of the coordinate q^i.

Given a smooth function

S : Q \to \mathbb{R}

the 1-form d S can be seen as a section of the cotangent bundle. The graph of this section is defined by the equation

\displaystyle{ p_i = \frac{\partial S}{\partial q^i} }

and this equation ties together two intuitions about ‘conjugate variables’: as coordinates on the cotangent bundle, and as partial derivatives of the quantity we’re trying to minimize or maximize.

The tautological 1-form

There is a lot to say here, especially about Legendre transformations, but I want to hasten on to a bit of symplectic geometry. And for this we need the ‘tautological 1-form’ on T^* Q.

We can think of d S as a map

d S : Q \to T^* Q

sending each point q \in Q to the point (q,p) \in T^* Q where p is defined by the equation we just saw:

\displaystyle{ p_i = \frac{\partial S}{\partial q^i} }

Using this map, we can pull back any 1-form on T^* Q to get a 1-form on Q.

What 1-form on Q might we like to get? Why, d S of course!

Amazingly, there’s a 1-form \alpha on T^* Q such that when we pull it back using the map d S, we get the 1-form d S—no matter what smooth function d S we started with!

Thanks to this wonderfully tautological property, \alpha is called the tautological 1-form on T^* Q. You should check that it’s given by the formula

\alpha = p_i dq^i

If you get stuck, try this.

So, if we want to see how much S changes as we move along a path in Q, we can do this in three equivalent ways:

• Evaluate S at the endpoint of the path and subtract off S at the starting-point.

• Integrate the 1-form d S along the path.

• Use d S : Q \to T^* Q to map the path over to T^* Q, and then integrate \alpha over this path in T^* Q.

The last method is equivalent thanks to the ‘tautological’ property of \alpha. It may seem overly convoluted, but it shows that if we work in T^* Q, where the conjugate variables are accorded equal status, everything we want to know about the change in S is contained in the 1-form \alpha, no matter which function S we decide to use!

So, in this sense, \alpha knows everything there is to know about the change in Hamilton’s principal function in classical mechanics, or the change in entropy in thermodynamics… and so on!

But this means it must know about things like Hamilton’s equations, and the Maxwell relations.

The symplectic structure

We saw last time that the fundamental equations of classical mechanics and thermodynamics—Hamilton’s equations and the Maxwell relations—are mathematically just the same. They both say simply that partial derivatives commute:

\displaystyle { \frac{\partial^2 S}{\partial q^i \partial q^j} = \frac{\partial^2 S}{\partial q^j \partial q^i} }

where S: Q \to \mathbb{R} is the function we’re trying to minimize or maximize.

I also mentioned that this fact—the commuting of partial derivatives—can be stated in an elegant coordinate-free way:

d^2 S = 0

Perhaps I should remind you of the proof:

d^2 S = d \left( \displaystyle{ \frac{\partial S}{\partial q^i} dq^i } \right) = \displaystyle{ \frac{\partial^2 S}{\partial q^j \partial q^i} dq^j \wedge dq^i }

but

dq^j \wedge dq^i

changes sign when we switch i and j, while

\displaystyle{ \frac{\partial^2 S}{\partial q^j \partial q^i}}

does not, so d^2 S = 0. It’s just a wee bit more work to show that conversely, starting from d^2 S = 0, it follows that the mixed partials must commute.

How can we state this fact using the tautological 1-form \alpha? I said that using the map

d S : Q \to T^* Q

we can pull back \alpha to Q and get d S. But pulling back commutes with the d operator! So, if we pull back d \alpha, we get d^2 S. But d^2 S = 0. So, d \alpha has the magical property that when we pull it back to Q, we always get zero, no matter what S we choose!

This magical property captures Hamilton’s equations, the Maxwell relations and so on—for all choices of S at once. So it shouldn’t be surprising that the 2-form

\theta = d \alpha

is colossally important: it’s the famous symplectic structure on the so-called phase space T^* Q.

Well, actually, most people prefer to work with

\omega = - d \alpha

It seems this whole subject is a monument of austere beauty… covered with minus signs, like bird droppings.

Example 6. In classical mechanics, let

Q = X \times \mathbb{R}

as in Example 1. If Q has local coordinates q^i, t, then T^* Q has these along with the conjugate variables as coordinates. As we explained, it causes little trouble to call these conjugate variables by the same names we used for the partial derivatives of S: namely, p_i and -H. So, we have

\alpha = p_i dq^i - H d t

and thus

\omega = dq^i \wedge dp_i - dt \wedge dH

Example 7. In thermodynamics, let

Q = \mathbb{R}^2

as in Example 3. If Q has coordinates S, V then the conjugate variables deserve to be called T, -P. So, we have

\alpha = T d S - P d V

and

\omega = d S \wedge d T - d V \wedge d P

You’ll see that in these formulas for \omega, variables get paired with their conjugate variables. That’s nice.

But let me expand on what we just saw, since it’s important. And let me talk about \theta = d\alpha, without tossing in that extra sign.

What we saw is that the 2-form \theta is a ‘measure of noncommutativity’. When we pull \theta back to Q we get zero. This says that partial derivatives commute—and this gives Hamilton’s equations, the Maxwell relations, and all that. But up in T^* Q, \theta is not zero. And this suggests that there’s some built-in noncommutativity hiding in phase space!

Indeed, we can make this very precise. Consider a little parallelogram up in T^* Q:

Suppose we integrate the 1-form \alpha up the left edge and across the top. Do we get the same answer if integrate it across the bottom edge and then up the right?

No, not necessarily! The difference is the same as the integral of \alpha all the way around the parallelogram. By Stokes’ theorem, this is the same as integrating \theta over the parallelogram. And there’s no reason that should give zero.

However, suppose we got our parallelogram in T^* Q by taking a parallelogram in Q and applying the map

d S : Q \to T^* Q

Then the integral of \alpha around our parallelogram would be zero, since it would equal the integral of d S around a parallelogram in Q… and that’s the change in S as we go around a loop from some point to… itself!

And indeed, the fact that a function S doesn’t change when we go around a parallelogram is precisely what makes

\displaystyle { \frac{\partial^2 S}{\partial q^i \partial q^j} = \frac{\partial^2 S}{\partial q^j \partial q^i} }

So the story all fits together quite nicely.

The big picture

I’ve tried to show you that the symplectic structure on the phase spaces of classical mechanics, and the lesser-known but utterly analogous one on the phase spaces of thermodynamics, is a natural outgrowth of utterly trivial reflections on the process of minimizing or maximizing a function S on a manifold Q.

The first derivative test tells us to look for points with

d S = 0

while the commutativity of partial derivatives says that

d^2 S = 0

everywhere—and this gives Hamilton’s equations and the Maxwell relations. The 1-form d S is the pullback of the tautologous 1-form \alpha on T^* Q, and similarly d^2 S is the pullback of the symplectic structure d\alpha. The fact that

d \alpha \ne 0

says that T^* Q holds noncommutative delights, almost like a world where partial derivatives no longer commute! But of course we still have

d^2 \alpha = 0

everywhere, and this becomes part of the official definition of a symplectic structure.

All very simple. I hope, however, the experts note that to see this unified picture, we had to avoid the most common approaches to classical mechanics, which start with either a ‘Hamiltonian’

H : T^* Q \to \mathbb{R}

or a ‘Lagrangian’

L : T Q \to \mathbb{R}

Instead, we started with Hamilton’s principal function

S : Q \to \mathbb{R}

where Q is not the usual configuration space describing possible positions for a particle, but the ‘extended’ configuration space, which also includes time. Only this way do Hamilton’s equations, like the Maxwell relations, become a trivial consequence of the fact that partial derivatives commute.

But what about those ‘noncommutative delights’? First, there’s a noncommutative Poisson bracket operation on functions on T^* Q. This makes the functions into a so-called Poisson algebra. In classical mechanics of a point particle on the line, for example, it’s well-known that we have

\begin{array}{ccr} \{ p, q \} &=& 1 \\ \{ H, t \} &=& -1 \end{array}

In thermodynamics, the analogous relations

\begin{array}{ccr} \{ T, S \} &=& 1 \\ \{ P, V \} &=& -1 \end{array}

seem sadly little-known. But you can see them here, for example:

• M. J. Peterson, Analogy between thermodynamics and mechanics, American Journal of Physics 47 (1979), 488–490.

at least up to one of those pesky minus signs! We can use these Poisson brackets to study how one thermodynamic variable changes as we slowly change another, staying close to equilibrium all along.

Second, we can go further and ‘quantize’ the functions on T^* Q. This means coming up with an associative but noncommutative product of these function that mimics the Poisson bracket to some extent. In the case of a particle on a line, we’d get commutation relations like

\begin{array}{lcr} p q - q p &=& - i \hbar \\ H t - t H &=& i \hbar \end{array}

where \hbar is Planck’s constant. Now we can represent these quantities as operators on a Hilbert space, the uncertainty principle kicks in, and life gets really interesting.

In thermodynamics, the analogous relations would be

\begin{array}{ccr} T S - S T &=& - i \hbar \\ P V - V P &=& i \hbar \end{array}

The math works just the same, but what does it mean physically? Are we now thinking of temperature, entropy and the like as ‘quantum observables’—for example, operators on a Hilbert space? Are we just quantizing thermodynamics?

That’s one possible interpretation, but I’ve never heard anyone discuss it. Here’s one good reason: as Blake Stacey pointed out below, these equations don’t pass the test of dimensional analysis! The quantities at left have units of energy, while Plank’s constant has units of action. So maybe we need to introduce a quantity with units of time at right, or maybe there’s some other interpretation, where we don’t interpret the parameter \hbar as the good old-fashioned Planck’s constant, but something else instead.

And if you’ve really been paying attention, you may wonder how quantropy fits into this game! I showed that at least in a toy model, the path integral formulation of quantum mechanics arises, not exactly from maximizing or minimizing something, but from finding its critical points: that is, points where its first derivative vanishes. This something is a complex-valued quantity analogous to entropy, which I called ‘quantropy’.

Now, while I keep throwing around words like ‘minimize’ and ‘maximize’, most everything I’m doing works just fine for critical points. So, it seems that the apparatus of symplectic geometry may apply to the path-integral formulation of quantum mechanics.

But that would be weirdly interesting! In particular, what would happen when we go ahead and quantize the path-integral formulation of quantum mechanics?

If you’re a physicist, there’s a guess that will come tripping off your tongue at this point, without you even needing to think. Me too. But I don’t know if that guess is right.

Less mind-blowingly, there is also the question of how symplectic geometry enters into classical statics via the idea of Example 4.

But there’s a lot of fun to be had in this game already with thermodynamics.

Appendix

I should admit, just so you don’t think I failed to notice, that only rather esoteric physicists study the approach to quantum mechanics where time is an operator that doesn’t commute with the Hamiltonian H. In this approach H commutes with the momentum and position operators. I didn’t write down those commutation equations, for fear you’d think I was a crackpot and stop reading! It is however a perfectly respectable approach, which can be reconciled with the usual one. And this issue is not only quantum-mechanical: it’s also important in classical mechanics.

Namely, there’s a way to start with the so-called extended phase space for a point particle on a manifold X:

T^* (X \times \mathbb{R})

with coordinates q^i, t, p_i and H, and get back to the usual phase space:

T^* X

with just q^i and p_i as coordinates. The idea is to impose a constraint of the form

H = f(q,p)

to knock off one degree of freedom, and use a standard trick called ‘symplectic reduction’ to knock off another.

Similarly, in quantum mechanics we can start with a big Hilbert space

L^2(X \times \mathbb{R})

on which q^i, t, p_i, and H are all operators, then impose a constraint expressing H in terms of p and q, and then use that constraint to pick out states lying in a smaller Hilbert space. This smaller Hilbert space is naturally identified with the usual Hilbert space for a point particle:

L^2(X)

Here X is called the configuration space for our particle; its cotangent bundle is the usual phase space. We call X \times \mathbb{R} the extended configuration space for a particle on the line; its cotangent bundle is the extended phase space.

I’m having some trouble remembering where I first learned about these ideas, but here are some good places to start:

• Toby Bartels, Abstract Hamiltonian mechanics.

• Nikola Buric and Slobodan Prvanovic, Space of events and the time observable.

• Piret Kuusk and Madis Koiv, Measurement of time in nonrelativistic quantum and classical mechanics, Proceedings of the Estonian Academy of Sciences, Physics and Mathematics 50 (2001), 195–213.

• Part 1: Hamilton’s equations versus the Maxwell relations.

• Part 2: the role of symplectic geometry.

• Part 3: a detailed analogy between classical mechanics and thermodynamics.

• Part 4: what is the analogue of quantization for thermodynamics?

This entry was posted on Monday, January 23rd, 2012 at 1:09 pm and is filed under probability, publishing. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.

47 Responses to Classical Mechanics versus Thermodynamics (Part 2)

  1. Uwe Stroinski says:
    23 January, 2012 at 3:49 pm

    The trick is to start with a big Hilbert space L^2(\mathbb{R}^2) on which p,q,t, and H are all operators, then impose a constraint expressing H in terms of p and q, and then use that constraint to pick out states lying in a smaller Hilbert space.

    Esoteric or not, I would like to learn more about this trick. Can you please provide a reference or elaborate this a little further?

    Reply
  2. Blake Stacey says:
    23 January, 2012 at 4:22 pm

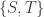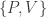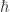    I was going to comment on the previous post about “quantizing” the Poisson brackets \{S, T\} and \{P, V\}, and how I had no idea what a formal statement like [P, V] = i\hbar actually means. (There’s an extra unit of time floating about somewhere, since \hbar is a quantum of action whilst conjugate variables in thermodynamics multiply to give energies, but I don’t think that’s a major point.) There goes my claim to priority on that statement of ignorance. . . .

    I’m not sure how the “quantized thermodynamics” one gets in this way relates to the quantum statistical physics I’ve studied before. Maybe they match up somehow, but it’s not clear to me. More thinking required!

    (Also, you’ve an extra dollar sign in the sentence beginning, “The trick is to start with a big Hilbert space”.)

    Reply
    • John Baez says:
      24 January, 2012 at 1:38 am

      In this blog entry I had said it was ‘fine’ to write [P,V] = i \hbar, not noticing that it was dimensionally incorrect. Thanks for catching that, Blake! This makes the issue even more interesting.

      I can’t stomach the thought of a blog article where I say it’s ‘fine’ to write down an impossible equation, so I’ve corrected this passage while giving you credit for noticing this.

      I’m not sure how the “quantized thermodynamics” one gets in this way relates to the quantum statistical physics I’ve studied before. Maybe they match up somehow, but it’s not clear to me. More thinking required!

      Yes, I don’t see how they’d match up neatly. In ‘quantized thermodynamics’ entropy is an operator; in ordinary quantum statistical mechanics it’s not. I think it’s time to google the phrase ‘entropy operator’.

      Reply
    • Blake Stacey says:
      24 January, 2012 at 4:08 pm

      Noted here for future reference:

      R. Gilmore (1985), “Uncertainty relations of statistical mechanics” Physical Review A 31: 3237–39, DOI:10.1103/PhysRevA.31.3237. Abstract:

      The product of the rms fluctuations of an extensive thermodynamic variable with that of its conjugate intensive thermodynamic variable is bounded below by k in the entropy representation and by kT in the energy representation. The uncertainty relations of statistical mechanics are equivalent to the stability relations of equilibrium thermodynamics.

      I believe the “energy representation” is closer to what we’ve been talking about. The bound on the right-hand side would then be the thermal Boltzmann energy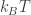 k_B T, instead of Planck’s constant.

      Maybe symplectic geometry is a way of talking about classical statistical mechanics in the limit where fluctuations are not quite negligible?

      Reply
    • John Baez says:
      25 January, 2012 at 7:30 am

      Hey thanks, Blake, that’s nice! Here are some thoughts before I break down and read the paper:

      It’s a bit mysterious. Here I’m using the analogy

      \begin{array} {ccccccc} q &\to& S & & p &\to & T \\ t & \to & V & & H &\to & P \end{array}

      This makes it odd to use the analogy

      \hbar \to k_B T

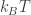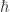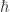      In other words, it’s odd to use k_B T as the analogue of \hbar in a formalism where T is not a constant but a variable! It would be analogous doing quantum mechanics in a setup where \hbar was proportional to the momentum operator p.

      (There are physicists who consider versions of quantum mechanics in which Planck’s constant becomes an operator, but I’ve never been remotely eager to join their ranks.)

      On the other hand, you’ll note that I have a slightly different analogy going on in my quantropy post! Over there I was quite happily using the analogy

      \hbar \to i k_B T

      So maybe this is what we need to do: study thermodynamics at fixed temperature, get a symplectic structure on the phase space of the remaining variables (for example volume and pressure, particle numbers and chemical potentials, etc.), and then ‘quantize’ it with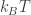 k_B T or maybe i k_B T playing the role of Planck’s constant.

      Maybe symplectic geometry is a way of talking about classical statistical mechanics in the limit where fluctuations are not quite negligible?

      That’s a nice thought. By the way, the weird intrusion of i in the analogy here:

      \hbar \to i k_B T

      reminds me of my formalism that unifies thermal fluctuations and quantum fluctuations as the real and imaginary parts of a complex-valued inner product on the tangent space of a manifold (here and here). However, in that setup, the thermal fluctuations are not described by a skew-symmetric tensor (like a symplectic structure), but rather a symmetric tensor.

      So in short, there are too many thoughts buzzing around my brain… on lucky days most of them fly away and one sits there long enough for me to catch it.

      Reply
  3. David Corfield says:
    23 January, 2012 at 5:24 pm

    Just to note before I have the chance to read this that symplectic geometry seems to be in the air in the math blogosophere at the moment.

    Reply
  4. Eric says:
    23 January, 2012 at 6:01 pm

    I really enjoyed this post. Thanks for writing it!

    The tautological 1-form reminds me of a tautological vector-valued 1-form, i.e. the identity map

    1 = \partial_i \otimes dx^i.

    Reply
    • John Baez says:
      24 January, 2012 at 1:42 am

      Glad you liked it. Yes, the tautological 1-form is a close relative of that vector-valued 1-form; not the same, but based on the same idea.

      Reply
      • amarashiki says:
        25 September, 2021 at 4:22 pm

        Tautological 1-forms are very “similar” to the closure relationship in Quantum Mechanics for Hilbert complete spaces. Sometimes I like to see closure relations as “generalized” 1-form tautological forms. Or are they the same in disguise?

        Reply
    • Eric says:
      25 January, 2012 at 4:52 am

      Interesting. We have

      1(\beta) = \beta

      for a 1-form \beta and

      1(X) = X

      for a vector field X, but feeding a 0-form f, we get

      1(f) = df.

      Given that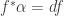 f^* \alpha = df, it makes me think there might be a commuting diagram hiding somewhere.

      Reply
  5. Nathan Reed says:
    24 January, 2012 at 8:12 am

    Interesting stuff! You say that the tautological 1-form “knows everything there is to know” about the mechanics, but it seems like such a trivial construction from the coordinates on T*Q…would it be fair to say that T*Q is what “knows” about the mechanics, i.e. the mechanics is encoded in the structure of the manifold? Or perhaps it’s the coordinates that “know” this, since alpha only has that nice formula in canonical coordinates on T*Q?

    BTW, you seem to have two “Example 5″s. :)

    Reply
    • John Baez says:
      25 January, 2012 at 6:42 am

      From the definition of the cotangent bundle T^* Q together with its map T^* Q \to Q, all else follows. I just wanted to emphasize the role of the tautological 1-form.

      Coordinates are not really required for mechanics; I only introduced them because people like them and in our examples they have exciting names like ‘position’, ‘momentum’, ‘time’, and ‘energy’.

      Thanks for catching the misnumbered example. I also tried to fix a bunch of minus signs in the commutation relations… but I also added some more examples, so there are probably some new mistakes too.

      Reply
  6. David says:
    24 January, 2012 at 2:49 pm

    I hope that you don’t mind off topic questions. I was mucking through the nits trying to understand this, and something bubbled up. Is a bilinear form the tool that we use to build up the concept of an ‘exact’ differential? [Which was a concept tossed at me in my undergraduate thermodynamics class, and contrasted with an inexact differential] [And so… are the Cauchy-Riemann equations constraints on a bilinear form?]

    Reply
    • John Baez says:
      25 January, 2012 at 4:48 am

      I’ve never thought of bilinear forms as a key tool to understanding the concept of exact differentials. To me what matters most is differential forms, which are something else, and extremely important throughout physics. There’s an operation d, the exterior derivative, that you can apply to any differential form \omega, and if \omega = 0 we say this differential form is ‘exact‘. An ‘exact differential’ is a slightly older name for an exact 1-form. (Differential forms come in various kinds: 0-forms, 1-forms, 2-forms, etcetera, and d of an n-form is an (n+1)-form.)

      All this is very good to study.

      And so… are the Cauchy-Riemann equations constraints on a bilinear form?

      I don’t think of them that way.

      Reply
  7. Jon Rowlands says:
    25 January, 2012 at 5:08 am

    Is example 2 OK? I can’t make the units work for the terms of dS.

    Reply
    • John Baez says:
      25 January, 2012 at 6:01 am

      Sorry, that example was screwed up. Thanks for catching my mistake! The formula should be

      \displaystyle{ d S = \frac{1}{T} d E - \frac{P}{T} d V }

      and the slight awkwardness of this formula is one reason people prefer the so-called ‘energy scheme’, where we talk about minimizing internal energy at fixed entropy and volume, rather than maximizing entropy at fixed energy and volume. Then we get

      d U = T d S - P d V

      and you’ll notice this formula, while nicer-looking, is equivalent to the previous one if we set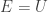 E = U, which is in fact correct: ‘internal energy’ is just I’d been calling ‘energy’ in Example 2.

      To fix this, I rewrote Example 2 and added a new Example 3.

      Reply
  8. John Baez says:
    25 January, 2012 at 7:05 am

    Over on Google+, Alexander Golden wrote:

    Something I’d be very interested in some sort of explanation relating for example Hamilton’s principal function and the entropy. Is there some operation or assumption that you can use to go from one to the other?

    I replied:

    Hamilton's principal function is basically just the action, so you should be happy if I can relate the principle of least action to the principle of maximum entropy.

    However this is a long story, because the principle of least action concerns classical dynamics, while the principle of maximum entropy concerns thermal statics. These are opposite corners of a square of theories:

    classical statics ——— classical dynamics

    thermal statics ———— quantum dynamics

    each apparently governed by its own minimum principle, maximum principle, or more generally, stationary principle (meaning that the first derivative of some quantity is zero). So, to get from one corner to the other we should understand all four:

    1) Classical statics is governed by the principle of minimum energy

    2) Thermal statics is governed by the principle of maximum entropy, or if we maximize entropy subject to a constraint on energy, minimum free energy.

    3) Classical dynamics is governed by the principle of least action.

    4) Quantum dynamics is apparently governed by the principle of stationary "quantropy", or if we look for stationary points of quantropy subject to a constraint on action, stationary "free action".

    The last item probably sounds very strange; the concepts in quotes are defined here, and I urge you to read this for some more details on what I’m getting at!

    Going from “thermal statics” to “quantum dynamics” involves a process of replacing temperature, or more precisely kT, by the square root of -1 times Planck’s constant, i \hbar.

    Going from “thermal statics” to “classical statics” involves taking the T \to 0 limit, so the principle of least free energy reduces to the principle of least energy.

    Going from “quantum dynamics” to “classical dynamics” involves taking the \hbar \to 0 limit, and then the principle of least free action should reduce to the principle of least action.

    I hope this helps! It takes a while to understand, and all the stuff about “quantropy” and “free action” is very new and not without problems.

    He replied:

    I was thinking more along the lines of, for example, could you state that the principle of least energy in the case of classical statics is sort of a “special case” of the principle of least action, but holding time constant? It seems like the units would work out correctly, since action is energy times time. So if that worked, that is, stable structures following a principle of least energy, would you possibly be able to place other restrictions on the action that would lead to the others? Or maybe starting with quantropy?

    I replied:

    It sounds like you’re suggesting that just as the principle of least energy in classical statics can be derived from the principle of least action in classical dynamics together with some extra assumptions, the principle of least entropy in thermal statics should be derivable from the principal of stationary quantropy in quantum dynamics together with some extra assumptions. That sounds worth trying, but I haven’t tried it! Thanks for the suggestion.

    (It’s probably better to say “stationary entropy” in the paragraph above, to make the analogy nicer and perhaps easier to work out. But I think the stationary points of entropy are all minima.)

    Reply
  9. Eric says:
    25 January, 2012 at 7:49 am

    Hi John,

    You might have noticed I’ve been writing a series of posts

    Network Theory and Discrete Calculus

    which largely follow what you are doing on this Azimuth blog, but formulated using discrete calculus. Your posts are providing interesting material faster than I can “discretize”.

    Of course, this post would be very fun to try to discretize, but one focus here is on coordinates. As you said, this is mostly to allow you to use interesting words for various components and is not really necessary for the physics. For me, it is easiest to discretize something expressed in a coordinate free manner.

    What would be a nice “coordinate free” example?

    I also really like what you said about Hamilton’s principle function and extended phase space. That resonates very well with discrete calculus and what I call “diamonation.”

    It would be fun to reformulate all these interconnections using discrete calculus.

    Reply
    • John Baez says:
      25 January, 2012 at 8:15 am

      Hi! Yes, I’ve been following your blog posts, but pretty distracted by other things.

      It would be good if you could discretize the concept of “cotangent bundle” and the “tautological 1-form” on this bundle. Here’s a nice coordinate-free formula for the tautological 1-form.

      For any manifold X there’s a map

      p: T^* X \to X

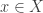      sending any cotangent vector \mu at the point x \in X to the point x. Differentiating this we get a map sending tangent vectors on T^* X to tangent vectors on X:

      dp: T(T^* X) \to T X

      The tautological 1-form \alpha on T^* X eats any tangent vector v at the point \mu \in T^* X and gives a number as follows:

      \alpha(v) = \mu(dp(v))

      It’s mind-blowingly tautological, eh? In case your brain starts to melt, it may help to keep in mind.

      x \in X

      \mu \in T^*_x X \subseteq T^* X

      v \in T_\mu (T^* X) \subseteq T (T^* X)

      I only recently noticed the more appealing but equivalent formulation I gave in the blog article, but it was already in Wikipedia.

      It’s a good exercise to see why the formula I just gave is equivalent to the tautological property of \alpha that I gave in my blog article, and also to the explicit coordinate-ridden formula I gave for \alpha. For anyone who gets stuck, Wikipedia gives some hints.

      Reply
      • Eric says:
        25 January, 2012 at 8:41 am

        Thanks for the challenge! However, I should manage expectations. I liked the extended phase space and the Hamilton-Jacobi approach precisely because it does not require defining (co)tangent spaces and I have a chance of formulating this discretely.

        The notion of cotangent space is tricky because there is no such thing as “covector at a point“. 1-forms are associated explicitly to 1-dimension edges and not to 0-dimensional points.

        I will try to do something sensible, but I may not have the maths chops.

        Reply
        • John Baez says:
          25 January, 2012 at 8:56 am

          The extended phase space is usually defined as the cotangent bundle of spacetime, or more generally, of the ‘extended configuration space’. See the Appendix in my blog article if you didn’t see it the first time: I added it later due to a question from Uwe.

          You should figure out some good analogue of a cotangent bundle if you want to do classical mechanics discretely. It will require creativity, but getting something like a tautologous 1-form and symplectic structure will be a sign you’re on the right track. It may be okay if cotangent vectors are associated to edges rather than points: after all, in the continuum limit these edges are very short so people with bad vision may have thought they were were points.

        • Eric says:
          25 January, 2012 at 9:19 am

          Oops! I misspoke. I did not mean “extended phase space”, but “extended configuration space”.

          I will take your advice and try to cook up a sensible discrete cotangent bundle, but I’d expect such a thing to allow a discrete calculus on it. Hmm…

          Thanks!

        • Eric says:
          25 January, 2012 at 10:17 am

          Some of the pictures here might be helpful:

          Discrete calculus on a 3-diamond and the discrete heat equation in n-dimension

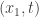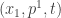          A 2-diamond is a toy model for a (directed) configuration space (x_1,t). A 3-diamond can either be a toy model for a (directed) configuration space (x_1,x_2,t) or possibly a (directed) phase space (x_1,p^1,t).

          The projections are obvious.

        • Florifulgurator says:
          25 January, 2012 at 2:48 pm

          You should figure out some good analogue of a cotangent bundle if you want to do classical mechanics discretely.

          What about Zariski cotangent space, which is constructed directly from the functions? (From this perspective cotangent space is the first thing, and tangent space comes later as the dual of cotangent space.)

        • aneumaier says:
          5 March, 2018 at 6:29 pm

          For discrete mechanics see, e.g., Marsden, J. E., & West, M. (2001). Discrete mechanics and variational integrators. Acta Numerica, 10, 357-514.

      • Eric says:
        26 January, 2012 at 3:11 pm

        I think I got it. It may take some time to write up. Thanks!

        Reply
  10. bob says:
    26 January, 2012 at 12:12 am

    Possibly relevant:

    http://arxiv.org/abs/0807.4632

    “We show that when the thermal wavelength is comparable to the spatial size of a system, thermodynamic observables like Pressure and Volume have quantum fluctuations that cannot be ignored. They are now represented by operators; conventional (classical) thermodynamics is no longer applicable…”

    http://arxiv.org/abs/math-ph/0703061

    “The physical variables of classical thermodynamics occur in conjugate pairs such as pressure/volume, entropy/temperature, chemical potential/particle number. Nevertheless, and unlike in classical mechanics, there are an odd number of such thermodynamic co-ordinates. We review the formulation of thermodynamics and geometrical optics in terms of contact geometry. The Lagrange bracket provides a generalization of canonical commutation relations. Then we explore the quantization of this algebra by analogy to the quantization of mechanics…”

    Reply
    • John Baez says:
      26 January, 2012 at 3:40 am

      Wow, thanks!

      (By the way, I can’t resist telling our readers that you are not the ‘bob’ that often posts here, namely
      Bob Coecke.)

      These papers look very relevant, especially the second one:

      • S. G. Rajeev, Quantization of contact manifolds and thermodynamics.

      He starts by wondering what could play the role of Planck’s constant in the analogy between thermodynamics and classical mechanics—exactly what Blake and I have been talking about.

      He emphasizes contact manifolds, which have already been mentioned in the comments to Part 1 of this series, by Matt Parry. So, Matt should read this! Personally while I like contact geometry and think it might be more fundamental than symplectic geometry, I consider them part of the same story.

      Here’s an ultra-quick introduction to the idea. In the classical mechanics of a point particle on the line I’ve been talking about a 4-dimensional manifold with coordinates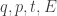 q, p, t, E (position, momentum, time, energy). This manifold comes with a 1-form

      \alpha = p d q - E d t

      and then the 2-form

      d \alpha = dp \wedge dq - d E \wedge d t

      is a ‘symplectic structure’, so our manifold becomes a ‘symplectic manifold’. But another approach is to treat Hamilton’s principal function S as a fifth independent coordinate. On this new 5-dimensional manifold there is a 1-form

      \beta = d S - p d q + E d t

      which is a ‘contact structure’, so this new manifold becomes a ‘contact manifold’.

      Similarly, in thermodynamics I’ve been working with the 4-dimensional manifold having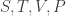 S, T, V, P (entropy, temperature, volume and pressure) as coordinates, but we can switch to a 5-dimensional manifold with the internal energy U as an extra coordinate—and this is a contact manifold.

      Reply
  11. Entropic Forces « Azimuth says:
    1 February, 2012 at 4:30 am

    […] Here my goal is to ponder a question raised by Allen Knutson: how does the ‘entropic force’ idea fit into my ruminations on classical mechanics versus thermodynamics? […]

    Reply

You can use Markdown or HTML in your comments. You can also use LaTeX, like this: $latex E = m c^2 $. The word 'latex' comes right after the first dollar sign, with a space after it.

This site uses Akismet to reduce spam. Learn how your comment data is processed.