I like it when people do interesting calculations and help me put their results on this blog. Renato Iturriaga has plotted a graph that raises some interesting questions about carbon dioxide in the Earth’s atmosphere. Maybe you can help us out!
The atmospheric CO2 concentration, as measured at Mauna Loa in Hawaii, looks like it’s rising quite smoothly apart from seasonal variations:
However, if you take the annual averages from here:
• NOAA Earth System Laboratory, Global Monitoring Division, Recent Mauna Loa CO2.
and plot how much the average rises each year, the graph is pretty bumpy. You’ll see what I mean in a minute.
In comparison, if you plot the carbon dioxide emissions produced by burning fossil fuels, you get a rather smooth curve, at least according to these numbers:
• U. S. Energy Information Administration Total carbon dioxide emissions from the consumption of energy, 1980-2008.
Renato decided to plot both of these curves and their difference. Here’s his result:
The blue curve shows how much CO2 we put into the atmosphere each year by burning fossil fuels, measured in parts per million.
The red curve shows the observed increase in atmospheric CO2.
The green curve is the difference.
The puzzle is to explain this graph. Why is the red curve roughly 40% lower than the blue one? Why is the red curve so jagged?
Of course, a lot of research has already been done on these issues. There are a lot of subtleties! So if you like, think of our puzzle as an invitation to read the existing literature and tell us how well it does at explaining this graph. You might start here, and then read the references, and then keep digging.
But first, let me explain exactly how Renato Iturriaga created this graph! If he’s making a mistake, maybe you can catch it.
The red curve is straightforward: he took the annual mean growth rate of CO2 from the NOAA website I mentioned above, and graphed it. Let me do a spot check to see if he did it correctly. I see a big spike in the red curve around 1998: it looks like the CO2 went up around 2.75 ppm that year. But then the next year it seems to have gone up just about 1 ppm. On the website it says 2.97 ppm for 1998, and 0.91 for 1999. So that looks roughly right, though I’m not completely happy about 1998.
[Note added later: as you’ll see below, he actually got his data from here; this explains the small discrepancy.]
Renato got the blue curve by taking the US Energy Information Administration numbers and converting them from gigatons of CO2 to parts per million moles. He assumed that that the atmosphere weighs 5 × 1015 tons and that CO2 gets well mixed with the whole atmosphere each year. Given this, we can simply say that one gigaton is 0.2 parts per million of the atmosphere’s mass.
But people usually measure CO2 in parts per million volume. Now, a mole is just a certain large number of molecules. Furthermore, the volume of a gas at fixed pressure is almost exactly proportional to the number of molecules, regardless of its composition. So parts per million volume is essentially the same as parts per million moles.
So we just need to do a little conversion. Remember:
• The molecular mass of N2 is 28, and about 79% of the atmosphere’s volume is nitrogen.
• The molecular mass of O2 is 32, and about 21% of the atmosphere’s volume is oxygen.
• By comparison, there’s very little of the other gases.
So, the average molecular mass of air is
28 × .79 + 32 × .21 = 28.84
On the other hand, the molecular mass of CO2 is 44. So one ppm mass of CO2 is less than one ppm volume: it’s just
28.84/44 = 0.655
parts per million volume. So, a gigaton of CO2 is about 0.2 ppm mass, but only about
0.2 × 0.655 = 0.13
parts per million volume (or moles).
So to get the blue curve, Renato took gigatons of CO2 and multiplied by 0.13 to get ppm volume. Let me do another spot check! The blue curve reaches about 4 ppm in 2008. Dividing 4 by 0.13 we get about 30, and that’s good, because energy consumption put about 30 gigatons of CO2 into the atmosphere in 2008.
And then, of course, the green curve is the blue one minus the red one:
Now, more about the puzzles.
One puzzle is why the red curve is so much lower than the blue one. The atmospheric CO2 concentration is only going up by about 60% of the CO2 emitted, on average — though the fluctuations are huge. So, you might ask, where’s the rest of the CO2 going?
Probably into the ocean, plants, and soil:
But at first glance, the fact that only 60% stays in the atmosphere seems to contract this famous graph:
This shows it taking many years for a dose of CO2 added to the atmosphere to decrease to 60% of its original level!
Is the famous graph wrong? There are other possible explanations!
Here’s a non-explanation. Humans are putting CO2 into the atmosphere in other ways besides burning fossil fuels. For example, deforestation and other changes in land use put somewhere between 0.5 and 2.7 gigatons of carbon into the atmosphere each year. There’s a lot of uncertainty here. But this doesn’t help solve our puzzle: it means there’s more carbon to account for.
Here’s a possible explanation. Maybe my estimate of 5 × 1015 tons for the mass of the atmosphere is too high! That would change everything. I got my estimate off the internet somewhere — does anyone know a really accurate figure?
Renato came up with a more interesting possible explanation. It’s very important, and very well-known, that CO2 doesn’t leave the atmosphere in a simple exponential decay process. Imagine for simplicity that carbon stays in three boxes:
• Box A: the atmosphere.
• Box B: places that exchange carbon with the atmosphere quite rapidly.
• Box C: places that exchange carbon with the atmosphere and box B quite slowly.
As we pump CO2 into box A, a lot of it quickly flows into box B. It then slowly flows from boxes A and B into box C.
The quick flow from box A to box B accounts for the large amounts of ‘missing’ CO2 in Renato’s graph. But if we stop putting CO2 into box A, it will soon come into equilibrium with box B. At that point, we will not see the CO2 level continue to quickly drop. Instead, CO2 will continue to slowly flow from boxes A and B into box C. So, it can take many years for the atmospheric CO2 concentration to drop to 60% of its original level — as the famous graph suggests.
This makes sense to me. It shows that the red curve can be a lot lower than the blue one even if the famous graph is right.
But I’m still puzzled by the dramatic fluctuations in the red curve! That’s the other puzzle.
Since I’m in Kansas, where we get a fair amount of snow from time to time, some winters being more snowy than others – and thus the following spring, there’s more of a recharge for the groundwater, which means that more grass and crops grow as opposed to drier winters in which less snow falls, maybe there’s a correlation between snowfall and CO2 levels in the atmosphere. In addition, ice crystals (and snowflakes) trap air and keep it close to the ground – maybe CO2 gets trapped in greater quantities than N2 and O2 in the H-O-H lattice…
You got a huge snowstorm there recently, right? So that would be on your mind. Year-to-year variations in weather worldwide might affect the CO2 concentration at Mauna Loa, both for reasons related to plant growth but also many other reasons. Just for fun I’d like to compare the CO2 concentrations to the El Niño Southern Oscillation, since that affects Pacific Ocean surface temperatures and warmer water might release CO2. I have no idea how significant this effect could be, but it would be amusing to check.
I have trouble believing that significant amounts of CO2 gets trapped in falling snow: even if a bit gets trapped, the total volume of the world’s snow must be quite puny compared to that of the atmosphere.
Methane clathrates, on the other hand, are a big deal!
How about this: http://peggy.uni-mki.gwdg.de/docs/kuhs/clathrate_hydrates.html ?
This doesn’t have a big enough effect to explain the graphs, but getting energy use data is quite non-trivial. It’s most probably being done primarily by tracking fuel being sold and assuming that’s being used. This has two big problems:
1. There’s a risk of fuel being sold illicitly, or getting confused and counting repeated sales of the same load of fuel.
2. Various nations strategic fossil fuel reserves may not be fully transparent.
So the blue curve may not be as smooth as shown. But not by anything like the magnitude needed to reconcile the two curves.
I took a quick look at chapter 10 (the perturbed carbon cycle) of David Archer’s book (which I think is a very useful reference for people with at least some training in the sciences). He claims that we put 7 Gtons C/yr in, of which 3 Gtons C/yr stays in the atmosphere, and 4 Gtons go into the land and the oceans (about 50/50). Uptake by the oceans imvolves multiple time scales (a short time scale for warm shallow water, a longer time scale for mixing with deep water, and an even longer time scale for conversion to CaC03).
Tracking fuel sold and treating it as all being used is a pretty fair assumption, given that storage capacity is well known, is fairly constant and stays that way, and figures for fuel in transit (usually by ship for oil and train for coal) are easily obtained.
Fuel use should increase as population increases, and that’s a fairly smooth curve (or has been).
Strategic fuel “reserves” are usually a classified or top-secret number, the public numbers are made-up nonsense, and they don’t matter anyway, because the fuel has to be extracted, first, mined and broken up into fine pieces as in coal, or produced at the wellhead as in crude oil, dewatered (usually), and desulfured (sometimes). What’s left in the ground is for all extents and purposes largely unknown, but it doesn’t enter the marketplace until extracted.
If you’re talking about things like the Strategic Ready Reserve or whatever that salt dome down in Louisiana is called, then that fuel isn’t on the market and probably won’t go on the market unless the armed forces allow it, which is unlikely. No oil and the military machine grinds to a halt, as Patton found in the winter of 1944/45.
As for public storage of fuel, that is easily estimated by counting coal piles, which you can do by looking at Google Earth, looking for power plants (they’re pretty generic) and then estimating the size of the coal pile(s) which will obey certain physical constraints usually being conical with a given limit to height vs diameter; and by counting crude oil tankers and tank farms, also using Google Earth.
As for using wood as a fuel, remember that burning green wood is difficult and that you’ve got to let it dry out for six months to a year, otherwise you can look to the rate of deforestation for this figure because most people don’t store appreciably sized woodpiles and it tend to rot away to compost.
I would have assumed an agency like the EIA would be looking at certain reported oil transactions, but to my understanding there’s some margin for unreported transactions.
The use of, eg, the US’s Strategic Petroleum Reserve has been used many times to smooth out local supply difficulties (so that oil that comes out eventually gets replaced). Even if the US has been fully transparent about its behaviour, it’s unclear whether reserves such as China’s strategic petroleum reserve have been used in similar ways.
So the point I was making was that just pulling the headline figures on fossil fuel sales can oversmooth the actual true behaviour. However, I wouldn’t think the magnitudes of the fluctuations would remotely be large enough to match the reported carbon dioxide concentations.
I’d guess the fluctuations are due to the oceans, just like temperature fluctuations. (Might be interesting to compare the two.) Estimates of anthropogenic carbon uptake by oceans seem difficult and sketchy – until that recent study: Can Ocean Carbon Uptake Keep Pace with Industrial Emissions?
[Emph. mine]
Graph:
Looks like jitter noise to me, for all the familiar reasons. Some of it real, some of it due to NOAA’s clumping, resampling, and detrending: “monthly mean”, “centered on the middle of each month”, “after correction”. Some oversampled (but still processed, not raw) data are available
ftp://ftp.cmdl.noaa.gov/ccg/co2/trends/co2_weekly_mlo.txt
The single best ad hoc annualizing of trend would be to take annual differences between corresponding pairs of smoothed points near each of the zero crossings of the known annual cycle – looks like around July and January.
A better analysis procedure would be to Butterworth filter out the annual contribution
http://en.wikipedia.org/wiki/Butterworth_filter
using an extremely narrow (hence the advantage of oversampling) annual bandpass. Then use the 5 point trapezoid filter (1 2 2 2 1) to eliminate most remaining jitter. Unfortunately I don’t have time today, maybe this weekend, but hopefully someone else can also do.
There’s nothing wrong with your atmospheric mass calculation; see this comment for a reference with a more precise number.
There isn’t really a contradiction between short-term interannual variability and the longer-term average response to an atmospheric carbon pulse. As you say, there are multiple time scales at work here.
I’m sure you’ve seen the large seasonal fluctuations in the Keeling CO2 curve, due mostly to terrestrial vegetation in the Northern Hemisphere. Likewise, you can get some similarly significant variability year-to-year due to vegetation dynamics (and also ocean dynamics).
The multidecadal response time in the “famous” graph (is it famous?) is due, for example, to the export of carbon from fast (“labile”) carbon pools to slower (“recalcitrant”) pools — i.e., litter carbon moving into the soil, more isolated from the atmosphere. This does not preclude seasonal and interannual variability, as (for example) gross photosynthesis grows and wanes. You just end up with a multidecadal decay curve with short-term fluctuations superimposed. Many of the vegetation fluctuations are climatic in origin (temperature and precipitation variability), or due to disturbance (fire, insect invasion, etc.). Of course disturbance itself is related to climate.
One good starting point is Le Quéré et al. (2009), Trends in the sources and sinks of carbon dioxide. You can also see Le Quéré et al. (2003), Two decades of ocean CO2 sink and variability; Schimel et al. (2001), Recent patterns and mechanisms of carbon exchange by terrestrial ecosystems; Schaefer et al. (2002), Effect of climate on interannual variability of terrestrial CO2 fluxes; Zeng et al. (2005), Terrestrial mechanisms of interannual CO2 variability. These aren’t necessarily the best references, but the first I turned up.
Thanks, Nathan! What you say makes sense. I’ll look at these references. It was fun trying to figure things out without reading anything, but now that my curiosity is picqued, I’m eager to see what the literature says.
I know it’s a bit risky to blog about climate science before I really understand it, but everyone’s doing it these days
, and I thought I’d try to set a good example by:
1) presenting data and calculations in a way that’s very easy to check and criticize,
and:
2) raising questions, rather than claiming to draw earth-shaking conclusions.
Yes, they’re visible in this blog entry. Anyone who doesn’t know what Nathan is talking about, just look at the red wiggles here, and the blowup in the lower right:
Renato wants to read the papers Nathan cited, but he doesn’t have access to the journals! Luckily, some are available for free if you just type the titles into Google and look around. For example:
• Le Quéré et al., Trends in the sources and sinks of carbon dioxide, Nature Geoscience, 2009.
There are some nice graphs in this paper, including figure a, which shows the rate of increase of CO2 concentration. This graph is jagged like Renato’s, but different, because it’s based on different data, also provide by NOAA:
There’s a lot of good information here, but they note that it would be good to have more:
Here’s another:
• Le Quéré et al., Two decades of ocean CO2 sink and variability, Tellus 55B (2003), 649–656.
The abstract:
(It says O2 there and I don’t think that’s a typo, though I don’t quite understand it — look at the end of section 4.)
There are also nice graphs here, but the story they tell seems to differ significantly from Le Quéré et al‘s more recent paper.
And another… it seems pretty easy to find all these papers for free:
• Schimel et al. Recent patterns and mechanisms of carbon exchange by terrestrial ecosystems, Nature 414 (8 November 2001), 169-172.
Again, more good graphs and information!
I believe that the starting point in this analysis is that the atmospheric CO2 level comes about from the impulse response of the CO2 uptake with the forcing function of the CO2 fossil fuel input combined with seasonal variations.
So if g(t) is the impulse response and f(t) is the forcing function, then the atmospheric content is the time convolution of f(t) with g(t).
The reason that the seasonal variations are still observed is that the convolution is essentially a low-band-pass filter and though it does filter the periodic signal, it doesn’t do it completely, and so we end up seeing the residual noisy oscillations in the Mauna Loa data.
There is also a time lag on the output of a convolution, and since g(t) has a significant fat-tail component, the convolved output keeps on accumulating, long after the forcing function is turned off.
I tried experimenting with the fossil fuel forcing function with a fat-tail CO2 impulse response function in a couple of blog posts last year:
http://mobjectivist.blogspot.com/2010/04/fat-tail-in-co2-persistence.html
http://mobjectivist.blogspot.com/2010/05/how-shock-model-analysis-relates-to-co2.html
I also combined these in a chapter of The Oil ConunDrum online book. I got interested in this topic because the oil production process can be described as a series of convolutions as well, and the CO2 residual is just another convolution stage in this process.
As William Feller said: “It is difficult to exaggerate the importance of convolutions in many branches of mathematics” from “An Introduction to the Probability Theory and its Applications”.
BTW, I found out that climate scientists understand convolutions very well but the knowledge of this technique amongst oil depletion analysts is very small.
Thanks, WebHubTel! I hadn’t wanted to bring convolutions into my already long blog post, but thinking about convolutions is precisely what made me so puzzled by the jaggedness of the red curve here:
I don’t think I can get that red curve by convolving the blue curve with any function
of the general sort shown here:
That is, some function
with with 
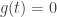for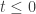 
and monotone decreasing for 
.
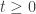WebHubTel wrote:
The variations in the red curve aren’t what I’d call ‘seasonal’: it’s wiggling around drastically at the 1-5 year scale. It would be nice to plot a graph of monthly averages, to see more detail.
But I like this aspect of your idea: if the production of CO2 by natural (as opposed to human) agents were very noisy, a low-pass filter might leave us with a curve like the red one. And it’s always worth remembering that natural processes produce and consume a lot more atmospheric CO2 than the human processes produce. So there’s potentially a lot of natural noise, with the blue curve as a small but significant signal buried in this natural noise.
Here’s another suggestion to think about (although sorry I’m feeling too lazy tonight to do it myself…)
The annual fluctuation that Nathan raised above is much larger than the annual mean increment. So the “rapid flux” into and out of the biosphere over the year is in effect the most rapid process. However, it’s likely that this has some variability from year to year, so that when you do the 12 month averaging you are going to end up with a signal containing effects from this variability. Another way of looking at it, if you Fourier transform theCO2 after removing the exponential growth you will get more than a simple 1 year peak – there will be a broader spread of energy. You might actually want to filter it out with a slightly better filter than a simple 12 month moving average in order to compare to the annual reported emissions – they are most likely estimates with some built-in smoothing from year to year anyway.
I read somewhere recently that the latest drought in the Amazon released as much CO2 as all the cars in the world. So presumably that will end up giving an upwards glitch in the red graph.
William T. said:
I think it has something to do with this. The averaging process is a low-band-pass filter and will suppress the noise, e.g. the classic Mauna Loa graph which is a cumulative averager. However, when we switch over to looking at year-over-year variations as in the incremental graph shown by Renato, we are essentially dealing with a derivative, which is a high-band-pass filter. In that case, any noise is accentuated and it starts looking more jagged.
OTOH, the energy production increments are likely based on data that is so filtered over time that the year-over-year increments turn very smooth. The derivative of this accentuates very little noise.
So I think this may be partially an artifact of how the CO2 data is collected and possible aliasing leading to derivative spikes and noise accentuation. We would really need to look at the original data.
This does require some thought as I now understand the concerns and see why John labelled it a “CO2 puzzle”.
Yes, it does have to do with the difference between natural source variation and equations, but you’ve missed the main reason for the difference.
The main reason is that an environment houses numerous simultaneously emerging and evolving systems, so best thought of as a kind of big pot of “pop corn” going off. It’s not “random” in that the large variations in locally developing events are just not connected at that scale. You don’t make progress with this subject unless you start asking questions about what animates these local developmental processes…
phil
Phil, Interesting to bring up the popcorn analogy. Many people presume that the popcorn going off is in some ways predictable. Yet, when food science researchers carefully measure the time it takes to pop for individually cooked kernels, they find that it generates a spread in times that is not even normally distributed, with obviously fatter tails. That’s why you find lots of unpopped kernels, as the variability is so large. I actually have a section on the phenomenon in The Oil ConunDrum. I looked into this because the popping of popcorn mimics both the temporal dynamics of searching for stuff like oil and of predicting the reliability of components. These are complements in the sense that success is the complement of failure. When you find a success (like an oil reservoir) or when you expose a failure is stochastic in mathematically similar ways.
I guess it further points to the great variability in natural processes.
It turns out that the popcorn hazard function
http://en.wikipedia.org/wiki/Survival_analysis
follows an extreme value (i.e. Gumbel) distribution. The reason is that the kernels that pop in a given interval (of increasing temperature) are simply the ones that were least likely to survive the interval. The details of the local processes (some slightly hotter, some slightly cracked) are irrelevant if reproducible.
Though I knew convolution was related to kernels, I never expected that popcorn has some relevance to climate change. Cool!
Well, actually, there’s a special kind of “kernel” that is especially useful for exposing the “pop corn” events hidden in the confusion of time series data. It doesn’t work automatically everywhere, but works astoundingly well some places. It involves the careful use of a smoothing kernel with a hole in the middle. A smoothing kernel with a hole in the middle preferentially reduces fluctuation for higher derivative rates, and so minimizes scalar distortion. It means you can find the true shape of the natural phenomenon, making the data more differentiable, and so expose their dynamics more graphically. It’s one of several mathematical tools I developed in the 80’s & 90’s for investigating locally emergent systems phenomena. http://www.synapse9.com/drwork.htm
I’d be happy to discuss is anyone is interested. Use the side bar to navigate or scroll down the page to the table of contents. I haven’t touched the thing in 10 years really as not a soul ever understood what it was about it seems.
A tiny detail …
John Baez, you say:
Box C: places that exchange carbon with the atmosphere and box A quite slowly.
Box A is the atmosphere.
Thanks – fixed!
The explanation “I came up with” was really what I understood from the article:
• Mason Inman, Carbon is forever, Nature Reports Climate Change, 20 November 2008.
The complete system of the CO2 consists in a lot cycles with different time scales, so more or less decoupled, each subcycle should have an equilibrium point which shifts as you pump CO2. So there is a subtlety difference between how may years will be in the air the CO2 that we just throw away and how many years will be the excess of CO2 once we stop pumping !
Just for the record, the data of the red curves comes from the data of December of each year, not from the average of the year.
Renato wrote:
Data for fossil fuel combustion is usually integrated over an entire year, so that the noise excursions in CO2 levels might be reduced by around a factor of 3 if you followed the same procedure and integrated over a yearly cycle. I believe that noise reduction would occur if the noise was IID and the improved counting statistics would reduce it by the square root of 12.
This will put the two sets of data on a more even footing at least.
Renato wrote:
Because the details seem to matter now:
If you got your data from here, your red curve does not exactly show the difference in CO2 concentration at Mauna Loa between one December and the previous one. It’s a difference of ‘corrected’ four-month averages:
I wish they explained the ‘correction’ method.
And while we are thinking about small but perhaps important issues: you could make me happier if you’d carefully check the 1998 data on your red curve:
Is it just some inaccuracy in the graphing program, or something else?
When you say “‘correction’ method”, do you refer to where they “corrected for the average seasonal cycle”?
I don’t know quite what that means. But I did look up what they do to remove the seasonal cycle. Maybe their ‘correction’ has something to do that. Thoning et al. (1989) describes the seasonal removal method (Sections 4.1-4.3). I don’t know if they’ve made any tweaks to the method since that paper was published.
They linearly detrend the gap-filled daily data, then apply a zero-padded fast Fourier transform. To remove the seasonal cycle, they apply a low-pass filter which is a decaying exponential of the fourth power of frequency (Eq. 2).
The filter has a “cutoff frequency” of 667 days (0.55 cycles/year), meaning the power is attenuated by half at a period of 667 days. 667 days was chosen so that the filter transfer function drops to almost zero right at a period of 1 year.
(They also talk about a 50-day filter to remove subseasonal variability, and it’s not entirely clear whether they apply that first before the seasonal filter, or whether that’s for a separate analysis.)
After filtering, they perform an inverse FFT back to the time domain, and add back the linear trend.
Nathan wrote:
Yes. Thanks for shedding some light on this! The passage I quoted is not very clearly written, but I’m betting that they’re talking about what you just explained.
There’s some speculation here (I mentioned it at his site; he pointed to this older thread)
Interesting! They took the CO2 concentration, subtracted off a seasonal cycle and a linear trend, and graphed what was left: the ‘anomaly’.
Then they compared the growth rate of this anomaly to the El Niño–Southern Oscillation, and got some intriguing correlations:
Let’s compare all this to the red curve on Renato’s graph:
It’s a bit hard to see what’s going on, but the 1997 peak in CO2 production stands out.
I guess my desire to compare Renato’s data to the El Niño–Southern Oscillation wasn’t completely silly!
John, I have to say that this is a most impressive bit of data forensics and scientific sleuthing that I have seen in a while.
The take away message has to be that the natural cycles and variations in CO2 can be momentarily large but as long as they don’t accumulate above the long-term average, they still pale in comparison to the relentless, almost monotonic, advance of man-made CO2 emissions.
Have you used a accumulative variance test to see if it’s a random walk? Or a variance suppression test to see if it’s an accumulative process?
Phil wrote:
I haven’t really done anything except explain what Renato Iturriaga did. The CO2 data is here — have at it!
But I’m not sure what you mean by ‘it’. The anomaly, I guess. For that, I think the most exciting thing is its apparent correlation with the “Niño-3 SST index”, as shown above. This is the sea surface temperature in a patch of the ocean fairly close to Hawaii:
Data for this region are available here — monthly since 1950 and weekly since 1990.
Oh, that’s easy, the “it” in this case is the physical process you are trying to describe, using the data recorded from it as a guide. The question of whether it is a statistical process or an overlay of many kinds of unrelated dynamic systems, or a single large scale system with small scale fluctuations.. etc. That would be important for knowing how to construct your mathematical description of it, wouldn’t it?
Those two tests described on my drstats.htm page would help answer those questions based on whether the trends visible have flowing change in their continuities, to being developing a case for it being one or another kind of natural phenomenon creating the data.
One can make a perfectly good statistical model of a dynamic system, but then it’s largely meaningless isn’t it, due to the mismatch in kind, right?.
I wonder if algal blooms are causing the difference. They should coincide with any significant influx of iron from stuff like upwelling during el nino, coastal runoff, dust from the Saharan and Mongolian deserts, and so on.
I don’t know how important algal blooms are here. This article seems relevant:
• R. A. Feely et al., The influence of El Niño on the equatorial Pacific contribution to atmospheric CO2 accumulation, Nature 398 (1999) 597–601.
Among other things, the abstract says:
Thanks, Hank! I’ve almost forgotten about tamino’s great blog (being too thrilled about this one). It’s actually no surprise he tackled similar analysis. There’s a lot to learn from tamino’s statistical data analysis blog posts.
I took the data from here
ftp://ftp.cmdl.noaa.gov/ccg/co2/trends/co2_mm_mlo.txt
The data for the red curve in 1998 is 2.76 this is from the difference of december 1998 and december 1997. There is no error inaccuracy in the graphing program. Only that the data is coming from december to december, not from the average. Since the data of the blue line comes on what happened on a given year I thought it was reasonable to take the same time intervals for the observed increment.
Renato wrote:
Okay, that explains my puzzlement. I’ll add a note to the blog entry explaining this.
What’s the best free software for graphing a lists of numbers? I want something that works on Windows. I think it would be fun to make a number of graphs related to this CO2 puzzle. For example, it would be fun to see the difference between your simple “December minus December” calculation and the more complicated calculation advocated by NOAA.
You might try SciDaVis which is specifically designed for plotting scientific graphs. It works pretty well. See:
http://scidavis.sourceforge.net/
Runs on Linux, Windows and Macs
Here’s a graph from Renato showing his original “December minus previous December” CO2 increases (in red) alongside the averaged and corrected figures advocated by NOAA (in yellow).
There’s not much difference, which is good.
I don’t know, I used microsoft excel, but I am no expert I think this is the first graph I make and it took me some time to figure out how excel works.
As far as free is concerned, OpenOffice works much like Excel. For graphing a list of numbers it’s pretty simple.
I use OpenOffice, avoiding software that I need to pay for, so I’ll give that a try. Now that I’m gradually ceasing to be a pure mathematician I need to learn how to draw pretty graphs — not just pretty commutative diagrams!
Use Sage then you can do both :-)
But seriously there is a good example by Marshall Hampton that uses exactly the same series.
For x-y graphs, Dplot plots well. The original version was free, but is now licensed etc. The Jr version might fit the bill.
http://download.cnet.com/DPlot-Jr/3000-2056_4-10784396.html
Concerning landuse flux (flows) Houghton has a series available at the CDIAC cdiac.ornl.gov site 1850-2005.
(they also have ocean data series.
diagram
here is the series URL for Houghton’s paper
http://cdiac.esd.ornl.gov/trends/landuse/houghton/houghton.html