I want to keep telling you about information geometry… but I got sidetracked into thinking about something slightly different, thanks to some fascinating discussions here at the CQT.
There are a lot of people interested in entropy here, so some of us — Oscar Dahlsten, Mile Gu, Elisabeth Rieper, Wonmin Son and me — decided to start meeting more or less regularly. I call it the Entropy Club. I’m learning a lot of wonderful things, and I hope to tell you about them someday. But for now, here’s a little idea I came up with, triggered by our conversations:
• John Baez, Rényi entropy and free energy.
In 1960, Alfred Rényi defined a generalization of the usual Shannon entropy that depends on a parameter. If is a probability distribution on a finite set, its Rényi entropy of order
is defined to be
where . This looks pretty weird at first, and we need
to avoid dividing by zero, but you can show that the Rényi entropy approaches the Shannon entropy as
approaches
1:
(A fun puzzle, which I leave to you.) So, it’s customary to define to be the Shannon entropy… and then the Rényi entropy generalizes the Shannon entropy by allowing an adjustable parameter
.
But what does it mean?
If you ask people what’s good about the Rényi entropy, they’ll usually say: it’s additive! In other words, when you combine two independent probability distributions into a single one, their Rényi entropies add. And that’s true — but there are other quantities that have the same property. So I wanted a better way to think about Rényi entropy, and here’s what I’ve come up with so far.
Any probability distribution can be seen as the state of thermal equilibrium for some Hamiltonian at some fixed temperature, say . And that Hamiltonian is unique. Starting with that Hamiltonian, we can then compute the free energy
at any temperature
, and up to a certain factor this free energy turns out to be the Rényi entropy
, where
. More precisely:
So, up to the fudge factor , Rényi entropy is the same as free energy. It seems like a good thing to know — but I haven't seen anyone say it anywhere! Have you?
Let me show you why it’s true — the proof is pathetically simple. We start with our probability distribution . We can always write
for some real numbers . Let’s think of these numbers
as energies. Then the state of thermal equilibrium, also known as the canonical ensemble or Gibbs state at inverse temperature
is the probability distribution
where is the partition function:
Since when
, the Gibbs state reduces to our original probability distribution at
.
Now in thermodynamics, the quantity
is called the free energy. It’s important, because it equals the total expected energy of our system, minus the energy in the form of heat. Roughly speaking, it’s the energy that you can use.
Let’s see how the Rényi entropy is related to the free energy. The proof is a trivial calculation:
so
at least for . But you can also check that both sides of this equation have well-defined limits as
.
The relation between free energy and Rényi entropy looks even neater if we solve for and write the answer using
instead of
:
So, what’s this fact good for? I’m not sure yet! In my paper, I combine it with this equation:
Here is the expected energy in the Gibbs state at temperature
:
while is the usual Shannon entropy of this Gibbs state. I also show that all this stuff works quantum-mechanically as well as classically. But so far, it seems the main benefit is that Rényi entropy has become a lot less mysterious. It’s not a mutant version of Shannon entropy: it’s just a familiar friend in disguise.

This is amazingly interesting and mysteriously easy.
I may point out a couple of points here as below.
In the formula, first of all, there must be a constraint that the energy should be positive definite. That is because the probability should be all the time smaller than one.
Secondly, when the system is in the ground state, ( goes to infinity), the free energy become Rényi entropy with
goes to infinity), the free energy become Rényi entropy with 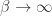 . If the energy is zero, then, the Reney entropy becomes infinity while conventional free energy should be zero at the ground state. This looks contradictory except when the ground state energy is not zero. I think the point is worthy to be discussed.
. If the energy is zero, then, the Reney entropy becomes infinity while conventional free energy should be zero at the ground state. This looks contradictory except when the ground state energy is not zero. I think the point is worthy to be discussed.
It seems that the physical interpretation of temperature should be carefully chosen if we equate the parameter for Rényi entropy to .
.
Wonmin wrote:
Good point. I wouldn’t call this a “constraint”: I’m starting with probabilities and defining the energies
and defining the energies 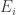 by
by
so it just works out automatically that
It’s not a constraint I have to impose But, it might be worth mentioning that the energies come out nonnegative.
You’re also right that the limits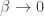 (infinite temperature, all states equally likely to be occupied) and
(infinite temperature, all states equally likely to be occupied) and  (zero temperature, only lowest-energy states occupied, and all of these equally likely) deserve special attention.
(zero temperature, only lowest-energy states occupied, and all of these equally likely) deserve special attention.
For one thing, these special limiting cases of Rényi entropy play a special role in understanding the work value of information. For another, the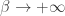 limit of Rényi entropy, called the min-entropy, is important in cryptography when we study a ‘worst-case scenario’ where a determined opponent is trying to break our code.
limit of Rényi entropy, called the min-entropy, is important in cryptography when we study a ‘worst-case scenario’ where a determined opponent is trying to break our code.
(The Shannon entropy, on the other hand, is related to an ‘average-case scenario’. This is okay for physics because — to coin a phrase — nature is subtle, but it’s not malicious.)
And, finally, it’s always good to study high- and low-temperature limits! Things often simplify here, and sometimes the high-temperature limit of one interesting physical system matches the low-temperature limit of another.
This post was mentioned on Twitter by Blake Stacey: http://bit.ly/e4gKsX
After kicking myself over not having thought of this — and getting a little entertainment from forwarding this to a colleague and watching him do the same — I thought, “Hey, I should see what Google Scholar knows about it.” After sifting through half a dozen false positives, I found Klimontovich (1995). Section 14.2 has, as equation (81),
where![S_\beta[p]](https://s0.wp.com/latex.php?latex=S_%5Cbeta%5Bp%5D&bg=ffffff&fg=333333&s=0&c=20201002) is Klimontovich’s notation for the Rényi entropy of order
is Klimontovich’s notation for the Rényi entropy of order  .
.
(Finding out why I did a double-take and had a wry chuckle after seeing where Klimontovich was published is left as an exercise for the interested reader.)
In turn, Klimontovich’s derivation appears to come largely from Beck and Schlogl’s Thermodynamics of Chaotic Systems (1993).
Darn. But thanks. I tried to find previous work on this subject, but I missed this.
I’d already let fly and put my paper on the arXiv; I’ll update it to include these references, an acknowledgement to you, and also some followup ideas I’ve had. At least it may help more people catch on! You’ve got a few people over here talking about maximizing Rényi entropy over here, and a lot of people talking about minimizing free energy over there, and they should get to know each other.
Heh.
I think there’s a lot to be said for (a) making previously obscure ideas less obscure and (b) showing that seemingly unrelated things are really connected.
Interesting. To shed some light on the physical meaning, maybe the following might help. If you set then
then 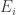 is dimensionless; if
is dimensionless; if  has to be an inverse energy (in units where Boltzmann’s constant
has to be an inverse energy (in units where Boltzmann’s constant 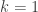 ) than
) than  does not make much sense. One can fix this by taking an arbitrary reference temperature
does not make much sense. One can fix this by taking an arbitrary reference temperature 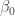 and define
and define
so that now one has . So 1) Rényi entropy might be related to the scaling of unit measures, and, who knows?, maybe it could even have some role when renormalizing… 2) when
. So 1) Rényi entropy might be related to the scaling of unit measures, and, who knows?, maybe it could even have some role when renormalizing… 2) when 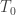 is just slightly more than
is just slightly more than  , one gets the temperature gradient which is the driving force of heat diffusion: could then Rényi entropy have some role out of equilibrium?
, one gets the temperature gradient which is the driving force of heat diffusion: could then Rényi entropy have some role out of equilibrium?
John wrote:
Sorry, I didn’t see that sentence. Forget my previous comment.
I won’t forget it — not because I’m one to hold a grudge, but because I actually think we can clarify the physics a bit by calling the standard temperature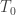 instead of 1. I mentioned this option in the last sentence of the first version of my paper, but I think it’ll be better if I show people what the resulting formulas actually look like, like your
instead of 1. I mentioned this option in the last sentence of the first version of my paper, but I think it’ll be better if I show people what the resulting formulas actually look like, like your
The mathematician in me is perfectly happy to set as many constants equal to 1 as I can get away with — but the physicist in me likes the look of this formula better than
This may be the first time I’ve acknowledged a tomato in a paper. Your blog may offer clues about your real identity, but Babelfish translates them as follows:
What’s an “emiliano”?
Is a “buontempone” someone who says “let the good times roll”?
Most importantly: is there one person named Tolomé Malatò Tempon, or three, or none?
(You can email me if this is top secret information — or ignore me if you want me to mind my own business! I just wish my Italian were up to reading this page.)
Tomate is correct, and it looks like the Renyi entropy is the secant of the temperature derivative of free energy. But this does not appear to be a gradient, it’s a normal equilibrium derivative.
If one starts from a completely general state with SI units
and uses for the Renyi parameter, one arrives at
for the Renyi parameter, one arrives at
The limit recovers
recovers
Which is from the first law
This has two uses
1. By calculating Renyi entropy in an equilibrated simulation running at temperature , one can get the free energy at
, one can get the free energy at 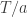 . This is useful if
. This is useful if 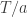 is, say, very close to absolute zero.
is, say, very close to absolute zero.
2. Protein chemists tend to use a non-differential form of the first law
This means that is actually
is actually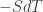 , and could perform better than the linear estimate. Of what practical significance this is, I have no idea.
, and could perform better than the linear estimate. Of what practical significance this is, I have no idea.
an exact expression which extrapolates
But! I think that is the interesting mathematics: what are functions where
where
is exact for all s, for some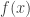 ?
?  stores information about
stores information about 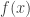 for every
for every  , such that if you know
, such that if you know  at a specific point
at a specific point 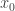 and you know
and you know 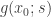 , you now know
, you now know 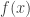 at EVERY point.
at EVERY point.
This is great stuff!
John asked:
It’s an inhabitant of the region Emilia-Romagna.
Everyone interested in these issues should check out Tomate’s blog entry on Rényi entropy and free energy.
Frederik explained what an “emiliano” is:
Tomate also emailed me and explained what a “buontempone” is: someone who likes to waste time, living a light and cheery life.
By the way, Renyi had a book on probability theory, that in the original Hungarian was entitled Valoszinusegszamitas (modulo accents). The German translation was entitled Wahrscheinlichkeitsrechnung. I have no point in telling you this, other than my amusement at foolishly long words.
So, you’d like the Rinderkennzeichnungs- und Rindfleischetikettierungsüberwachungsaufgabenübertragungsgesetz.
I find it pretty amusing to pick apart the etymology of the German title. The basic roots are “wahr”=”true”, “scheinen”=”to seem”, and “rechnen”=”to calculate” (cognate with English “to reckon”); the suffixes “-lich” and “-keit” are roughly equivalent to “-ly” and “-ness”. “wahrscheinlich”, literally “true-seeming”, is German for “probable” or “probably”, and “Wahrscheinlichkeit” is “probability”. Thus “Wahrscheinlichkeitsrechnung”, properly translated as something like “Computation of probabilities” or “The calculus of probability”, can be literally interpreted as “Reckoning about how true stuff seems to be”.
Those long German compounds look intimidating, but in some respects German is much friendlier to non-native speakers than English: complicated German words tend to be built out of simple German words, whereas complicated English words tend to be built out of Latin and Greek words.
Mark wrote:
By the way, I just noticed that the letter W on Boltzmann’s tomb in Vienna, which stands for entropy, really comes from the word Wahrscheinlichkeit.
I’ve always liked the French word vraisemblable, meaning likely or probable, and often heard in vraisemblablement, meaning probably. Vrai is true, sembler is to seem, and -able is more or less the same as in English. Semblable therefore means seem-able, or similar. Hence vraisemblable is true-seem-able, or true-similar, or probable.
That is nice. I never knew vraisemblable, since probability theory is usually instead referred to as “probabilités” in French. (The root here is apparently the Latin “probare”, “to test”.)
Title of Rényi’s book (with accents) is “Valószínűségszámítás” in Hungarian, I have a copy in my library. You may be interested in the structure of the word (which is usually translated as Probability Theory).
It is a compound word made of two parts, “valószínűség” and “számítás”.
Now, the first one is parsed like “való-szín-ű-ség”. In math it is a technical term and simply means “probability” but in common speech it has connotations like chance, feasibility, likelihood, odds, presumption, plausibility or verisimilitude.
As for its parts, “való” is the present participle of the substantive verb “van”. “Valódi” means actual, genuine, intrinsic, live, real, sheer, sterling, unimitative, something true to the core while “valóság” (like being-ness) is reality, actuality, deed, entity, positiveness or truth.
“Szín” is simply color, but also means tint, complexion, face or surface. The suffix “ű” makes an adjective of it (like tinct or colorous if there were a word like that) while “ség” corresponds to the English suffix -ness. All in all it is something having the complexion (or appearance) of reality.
The second one can be parsed as “szám-ít-ás”. “Szám” means number while the suffix “ít” makes a verb of it, so “számít” is to count or calculate (but also to matter or reckon). The suffix “ás” makes a noun again, “számítás” meaning calculus (but reckoning as well).
So the true meaning of the title is more like “Probability Calculus”.
By the way, there is not much about entropy in the book (none about Rényi entropy), it is only mentioned (and defined) twice in exercises, following chapters, as it is a (pretty good) textbook (written in 1966).
As you can see Hungarian words have quite some structure. I happen to know the guy (Gábor Prószéky) who is responsible for the Hungarian spell checker. He said it was utterly impossible to follow a dictionary approach to the problem, as he reckoned it would have required some 24 billion entries.
Once upon a time it was also part of my job to count Hungarian word forms and I came up with a slightly different lot, infinity. It really does not make much difference.
If you take a large volume of text from any language, order words according to decreasing frequency of occurrence and consider log frequency as a function of log rank, then after some initial fluctuation it usually settles to a straight line with negative slope of course. It means a distribution according to some power law and this feature looks quite universal. However, the exponent is not language-independent. For some languages it is below -1, so the larger the volume of text analyzed, the closer one gets to a full word list. On the other hand in Hungarian it is slightly above -1, so no matter how much text one takes, new words just keep trickling in. I guess it is a common feature of agglutinative languages including Navajo, Turkish or Finnish, although I have not checked them. By the way, at the sentence level all languages behave like this.
So the prerequisite of a Hungarian spell checker was an automatic morphological parser. And Dr. Prószéky (a mathematician and linguist) in fact had one for Hungarian well before applying it to a real life problem and going into business.
With such a language, no wonder native Hungarian speakers, starting from early childhood, have considerable practice in real time analysis of complex structures :)
Fascinating remarks, Berényi Péter! And they’re even related to the main topic of this blog post, information theory, since the statistical study of language — such as that linear ‘log frequency versus log rank’ relation you mentioned, called Zipf’s law — is connected to information theory!
While we’re at it: Hungarian is exciting and strange because it’s a Finno-Ugric language. Do other Finno-Ugric languages, like Finnish and Estonian, share the unusual properties you mentioned? I don’t know if they’re agglutinative like Hungarian.
(I could look it up, but I like to think that Google hasn’t yet made conversation obsolete!)
Yes, Zipf’s law. However, as a thorough theoretical understanding of this phenomenon is still missing, it is more like an empirical regularity than a law.
There may be an underlying critical state attained by Self Organized Criticality (SOC), like in Sandpile Avalanche Dynamics models. This kind of scale invariant behavior pops up in a wide variety of fields, including climate studies and may have connections to the somewhat mysterious Maximum Entropy Production Principle (MEPP) of (thermodynamically) open systems.
As for Hungarian, the language is generally considered to belong to the Finno-Ugric language family indeed. However, Finnish is not a close relative of Hungarian. Naïve native speakers of either language are unable to identify a single phrase of the other language, and the relation is only uncovered by deep lingustic analysis. By the way, I do not think so called language families evolved along the same path biological evolution followed. In genetics channels of information flow are highly regulated (for so called “higher species” it’s sex) while in memetics it is not, or at least if Bickerton’s research on Hawaiian Creole has merit, it is done in an entirely different way.
Therefore it is unlikely languages can be classified according to a 19th century dream about a well defined tree structure. In fact it looks like Hungarian has far reaching connections beyond the Finno-Ugric group including subgroups of the Altaic family like Turcic languages, possibly others as well. Some go as far as looking for connections to ancient Sumerian. Being a somewhat lunatic theory, it is not entirely out of the question though, because Sumerian used to be the lingua franca of the Middle East for three millenia and as such obviously had some influence on the surrounding regions, including the great plains north of the Caucasus Mountains. It was like Latin in medieval Europe (which happened to be the official language of the Hungarian Kingdom for eight hundred years).
As history was turbulent enough all over the world and populations got mixed intermittently, there must have been multiple episodes of partial pidginization followed by abrupt creolization (within a single generation) buried deep down below the surface of all conceivable languages.
I do not trust linguists too much, because I know how bone headed they can be. For example Dr. Prószéky used to work for the Linguistic Institute of HAS (Hungarian Academy of Sciences) in the early 1980s and was tasked with implementing the morphological ruleset of Hungarian in an automatic parser. By that time the science was considered long settled, so he was supposed to just formalize the rules found in textbooks, write some computer code that could interpret them and feed the program with plenty of text to see the result. And that’s what he did. However, the parsed output was full of all too obvious errors. He went back to the drawing board, repeatedly reformulated the ruleset, alas, to no avail, misparsed wordforms just kept coming. Finally he was forced to abandon textbook knowledge altogether and established a new utilitarian paradigm that judged the value of a ruleset based on its performance alone. The end result was a new ruleset, not akin to anything previously seen, that performed far better than the traditional one.
At that point he decided to publish his results, but met bitter resistance. The uproar was about his ruleset simply did not make sense at all from a linguistic point of view. People were absolutely unwilling to consider the possibility that in this case there might be some problem with linguistic theory itself.
As market demand for a good spell checker arose around the same time, he silently left Academia, started his own R+D company and developed one (with overwhelming success, one should say). Of course the product is built around the morphological ruleset he already had. The approach was developed further and now it is applicable to a wide range of linguistic problems and languages including syntactic analysis and machine translation. He is professor of language technology at Pázmány Péter Catholic University by now.
I am not an expert in Finnish, but I guess a good Finnish spell checker also needs a morphological parser. However, as soon as one goes beyond the word level, any natural language gets mind bogglingly complicated even if 3 years old kids seem to cope well with this kind of complexity.
Currently I am reading Bursts by Albert-László Barabási (another Hungarian, or Szekler, to be more precise). Besides being an awesome read in itself, also gives some insight into the field of complex networks and systems.
Berényi wrote:
It’s possible to derive Zipf’s law from information-theoretic assumptions:
• J. M. M. J. Vogels, Entropy related remarks on Zipf’s law for word frequencies.
It would be nice if this law arose from some tendency for communication to maximize information transfer. But there have been lots of other attempts to derive Zipf’s law, some of which are summarized in this paper. It’s even possible to get Zipf’s law in ‘completely random’ texts:
• Wentian Li, Random texts exhibit Zipf’s-law-like word frequency distribution
So, I don’t know what’s really going on with Zipf’s law.
I should warn you that we don’t allow insults on this blog, even of this fairly weak sort: “I know that in some large set there exist members
there exist members 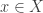 who are bone headed”. Insults tend to breed further insults, and distract from what I’m trying to do here.
who are bone headed”. Insults tend to breed further insults, and distract from what I’m trying to do here.
Zipf’s law is an example of a (probability disrbiution which is a) power law. One of the difficulties is that it can be difficult to show purely empirically that a power law is what the data is following (rather than, eg, a log-normal). So I’d be cautious in assessing with any “explanatory but non-predictive” theories which require the istribution to be a power law (rather than a weaker property like being heavy tailed).
And, of course, “It’s a power law!” is hardly the end of any story, even if it’s true (that is, even if you haven’t fooled yourself by doing sloppy statistics, or constructed a meaningless network by forgetting the actual chemistry or biology of the thing you’re trying to study).
For example, everybody loves “scale-free networks”: collections of nodes and links in which the probability that a node has connections falls off as a power-law function of
connections falls off as a power-law function of  . But the degree distribution does not by itself characterize a network! Two networks can be quite different but have identical degree distributions. For example, consider the “clustering coefficient”, defined as the probability that two neighbours of a node will themselves be directly connected. (It measures the “cliquishness” of the network, in a way.) One can build networks with indistinguishable power-law degree distributions but arbitrarily different clustering coefficients.
. But the degree distribution does not by itself characterize a network! Two networks can be quite different but have identical degree distributions. For example, consider the “clustering coefficient”, defined as the probability that two neighbours of a node will themselves be directly connected. (It measures the “cliquishness” of the network, in a way.) One can build networks with indistinguishable power-law degree distributions but arbitrarily different clustering coefficients.
The NetworkX Python module has a built-in function to do just this: powerlaw_cluster_graph().
native speakers of either language are unable to identify a single phrase of the other language
I was taught that the common vocabulary was about body parts and fish, such that there was some sentence about grabbing a fish with one’s hand that was comprehensible to speakers of either language.
David used to study statistical inference and machine learning, and this led him to become interested in some variants of the ordinary notion of entropy. So, anyone interested should read his old blog posts on Tsallis entropy and Rényi entropy. I just remembered these posts now. They have some nice references that I should reread, like this:
• Peter Harremöes, Interpretations of Renyi entropies and divergences.
I’ve explained relative entropy here. Harremöes shows that the ‘Rényi divergence’, or relative Rényi entropy, measures how much a probabilistic mixture of two codes can be compressed.
Relative Rényi entropy is also discussed here:
• E. Lutwak, D. Yang and G. Zhang, Cramer-Rao and moment-entropy inequalities for Renyi entropy and generalized Fisher information, IEEE Transactions on Information Theory 51 (2005). 473-478.
and I’m sure in dozens of other papers — but I just happen to be getting interested in Cramer-Rao inequalities, so this is nice.
By the way, I think the name ‘Harremöes’ is really cool. It reminds me of Averröes. I didn’t think people had cool names like that anymore. ‘Averröes’ was a Latinization of Ibn Rushd, although this philosopher was also known as Ibin-Ros-din, Filius Rosadis, Ibn-Rusid, Ben-Raxid, Ibn-Ruschod, Den-Resched, Aben-Rassad, Aben-Rois, Aben-Rasd, Aben- Rust, Avenrosdy Avenryz, Adveroys, Benroist, Avenroyth, Averroysta, and “Hey, you! Philosopher dude!”
This is really a reply to your n-Café post, but I see you’re disallowing comments there, presumably so that they’re all in one place here.
Anyway, you point out there a couple of previous blog posts by David Corfield on Rényi entropy and its close relative, Tsallis entropy. I just wanted to point out another n-Café post where Rényi entropy came up: Entropy, Diversity and Cardinality (Part 1).
While I’m writing, here’s a historical note on what physicists call “Tsallis entropies”.
As far as I know, they were first discovered in the context of information theory:
• J. Havrda and F. Charvát, Quantification method of classification processes: Concept of structural alpha-entropy. Kybernetika 3 (1967), 30-35.
(It’s a Czech journal which I had some trouble getting hold of; my friend Jirka Velebil in Prague found a copy for me.) There’s a slight caveat here: they were working with logarithms to base 2, as information theorists are wont to do, and accordingly the expression looks a bit different.
I’ve read somewhere that they were independently discovered around the same time (I think a year or two later) by Z. Daróczy. They are certainly studied in the book
• J. Aczél, Z. Daróczy, On Measures of Information and Their Characterizations. Academic, New York, 1975.
In general, this is an excellent reference for entropies of all different kinds (including Rényi). If you ever want a unique characterization theorem for a pre-1975 entropy, you’re very likely to find it here.
The Havrda-Charvát entropies were rediscovered in statistical ecology in the 1980s:
• G.P. Patil and C. Taillie, Diversity as a concept and its measurement. Journal of the American Statistical Association 77 (1982), 548-561.
This time it’s to base e, so the formula is exactly the same as the one used by Tsallis when he rediscovered them (again!) in physics in 1988:
• C. Tsallis, Possible generalization of Boltzmann-Gibbs statistics. Journal of Statistical physics 52 (1988), 479-487.
There remains the question of what to call these things. If you’re writing for physicists I suppose you call them “Tsallis entropies”, because (a) although he was by no means first to write down the formula or study it mathematically, he was apparently first to see its physical significance, (b) historical priority never stopped something being named after the wrong person anyway, and (c) everyone else does. If you’re not writing for physicists, it’s up to you.
Of course, the Havrda-Charvát-Daróczy-Patil-Taillie-Tsallis entropies are a simple transformation of the Rényi entropies, which came earlier than any of them.
Thanks for all those references, Tom! I’ve been crossposting a bit between here and the n-Café, but only allowing comments at one place, since it seems a bit silly to have separate conversations in two rooms about the same subject. Information theory here, category theory there — that’s how I’m trying to handle it.
Your references are really helpful… I need to get to the bottom of some questions, now. Like this:
If Tsallis was trying to generalize Boltzmann-Gibbs statistics (∼ ordinary statistical mechanics) by replacing ordinary entropy with Tsallis entropy, and Tsallis entropy is a simple transform of the Rényi entropy, and Rényi entropy is just a fudge factor times the free energy (a well-known concept in ordinary statistical mechanics), isn’t there perhaps less going on here than meets the eye? A lot of smoke and gunfire, but fewer concepts shooting it out than you might think?
Was perhaps Tsallis secretly just replacing the principle of maximum entropy by the principle of minimum free energy?
That would be odd: it would make his work seem unnecessary. The idea of minimizing free energy goes back to Gibbs, and it amounts to maximizing entropy subject to a constraint: a well-understood idea among physicists.
Presumably there’s something more to Tsallis’ work than this, but perhaps my null hypothesis should be that there’s not.
But what to do when they happen at the same time? I was trying to figure out a category theoretic version of Bayesian networks here. Now I see Coecke and Spekkens are applying the picture calculus of monoidal categories to Bayesian inference.
I wonder if their work gives a category-theoretic foundation to the existing theory of Bayesian networks. That’s one thing I want to do. I’d completely forgotten you wanted to do it!
If you put Coecke and Spekkens together with Harper, I suppose you discover that, in the properly simplified scenario, natural selection happens in a dagger-compact category with commutative Frobenius structure.
Hi John. Personally I tend to recoil a little bit when people send me references, because although of course it can be extremely helpful, I can’t suppress the small voice saying “oh no! now I have to look them up!” But perhaps you’re made of sterner stuff.
Anyway, I guess my main points were (i) that Tsallis entropy is in some sense a misnomer (the main reason for giving most of those references), and (ii) the book by Aczel and Daróczy is pretty useful for entropy characterization theorems.
I won’t presume to pronounce on the physics of it. But for the purposes I’m interested in, I tend to regard the fundamental quantity as not Tsallis entropy, nor Rényi entropy, but the exponential of Rényi entropy. Some reasons are sketched in that Café post I cited, where I call this quantity “cardinality” (of order ). Thus, a uniform probability distribution on a set of cardinality n has cardinality n.
). Thus, a uniform probability distribution on a set of cardinality n has cardinality n.
But then the “fudge factor” that you mention becomes what I suppose we must call a “fudge power”, which sounds a bit less innocuous, and also like a sugar high.
Seems to me like Tsallis entropy is for when you don’t really know how to count DoFs.
That makes some sense. I have read that Tsallis entropy is used when you want to explain a power-law distribution. But then again you can always generate a power-law by invoking a ratio distribution argument on two exponentials, which essentially says that you are adding DOF to the system.
Tom wrote:
Do you remember if it gives some nice theorems that single out the Rényi entropies? This reference:
• J. Uffink, Can the maximum entropy principle be explained as a consistency requirement?, Sec. 6: Justification by consistency: Shore and Johnson, Stud. Hist. Phil. Sci. B26 (1995), 223-261.
shows that Shore and Johnson’s attempt to characterize the usual Shannon entropy by a certain list of axioms actually fails, but succeeds in characterizing Rényi entropies in general. I would like to see more theorems like this!
I happen to have the book by Aczel and Daróczy in front of me (as it happens, because Tom pointed me to it), so I can tell you that they show Rényi entropies are the only additive entropies in some more general class. Some of the technical results in the same section address quite directly your question below: “what’s so great about raising a probability to a power?”
This preprint which appeared this morning (and was co-authored by a mathematical sibling of mine) doesn’t mention entropy explicitly but is about a characterization of norms which appears to be closely related.
norms which appears to be closely related.
As Mark just said, yes, the book of Aczél and Daróczy has at least one characterization theorem for Rényi entropies. I think it’s the same as the one Rényi gave in his original paper introducing his entropies.
I don’t know whether I’d use the word “nice”. My current impression (based on only superficial browsing) is that this theorem concerns what Rényi calls “incomplete probability distributions”, i.e. vectors with
with  and
and 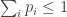 . Personally I’d prefer a theorem that stuck to ordinary distributions (
. Personally I’d prefer a theorem that stuck to ordinary distributions (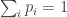 ). But maybe I’m not seeing the point.
). But maybe I’m not seeing the point.
However, I’ve just been looking at a different characterization:
• R.D. Routledge, Diversity indices: which ones are admissible? Journal of Theoretical Biology 76 (1979), 503-515.
This characterizes the Hill numbers, which are simply what ecologists call the exponential of the Rényi entropies. To my mind, it seems a more satisfying result, but I don’t have the energy to explain what it says right now.
I think (also based on only superficial browsing) that Aczél and Daróczy give multiple characterization theorems for Rényi entropies. One is Rényi’s theorem involving functionals of “incomplete probability distributions”, but they have another characterization that only deals with ordinary distributions. The tradeoff is that the latter result makes stronger assumptions on the nature of the functional, restricting to what they call “average entropies”.
Thanks; I’ll take a look.
Incidentally, my copy of Aczél and Daróczy makes me a little bit sad. It’s out of print, so I ordered a second-hand copy from Amazon, and when it arrived it turned out that it used to belong to a university library (Wright State University in Ohio). So they, presumably, no longer have a copy of this nice book. Also, whereas the price to me was quite substantial, I bet they made at most a trivial amount of money from selling it.
Tom wrote:
Yes, that is sad. Kinda like buying jewelry and finding it was pawned by a now-destitute queen.
But most libraries sell books not to make money, but to clear out space. They are constantly short of space. Books not sufficiently used eventually get weeded out. So if you want to feel sorry for Wright State University, you should probably feel sorry that they can’t afford to expand their library. At least the book went to someone who will appreciate it!
The U. C. Riverside library is suffering a severe space shortage, and it’ll only get worse with the proposed $500 million budget cut for the University of California system. On the “bright side”, we’re too broke to buy many new books: the library can’t easily reduce expenditures on journals, thanks to journal bundling, so the books and library staff take most of the budget hit.
Here’s a half-baked idea which I’ve had in my head for a while. I’m posting this here in the hope that someone knows about this.
To begin, it is old hat that every permutation-invariant polynomial in the variables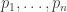 can be written as a polynomial of the power sums
can be written as a polynomial of the power sums
where we take to range over the naturals.
to range over the naturals.
Now, is there an analogous statement for permutation-invariant functions, where then would be allowed to range over the positive reals? Which class of functions would one choose to do this?
would be allowed to range over the positive reals? Which class of functions would one choose to do this?
In other words, given any ‘natural’ function of the probabilities, can it be written as a function of the Rényi entropies?
Hi, Tobias!
Yes, and it was thinking about this that led me to realize the relation between Rényi entropy and free energy. Maybe I should mention this in my paper.
The idea goes like this. The probabilities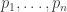 can be recovered from the energies
can be recovered from the energies 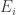 such that
such that
and these energies can be recovered from the ‘density of states’
The Laplace transform of the density of states is the partition function:
so the density of states can be recovered by taking the inverse Laplace transform of the partition function.
Thus, you can recover the probabilities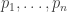 if you know the partition function for all
if you know the partition function for all  .
.
But you can recover the partition function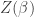 if you know the Rényi entropy
if you know the Rényi entropy  , thanks to my calculation above:
, thanks to my calculation above:
So, the Rényi entropies for
for  determine the probabilities
determine the probabilities 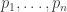 , up to a permutation.
, up to a permutation.
Nice! That is certainly the more natural way to phrase it, although my formulation sounds much more sophisticated ;)
Maybe someone would like to comment on the general “law of continuity” I found a few years ago. It follows directly from energy conservation, that it takes the work of evolving a process to make any change. That then implies there are lots of missing variables from the equations we assume apply to any phenomenon involving energy use, for what amount to the other components of entropy. The main one is the component of “entropy” that must necessarily be the energy used to build the system for using energy referred to.
When you check out that basic map with observation, that all events require energy to build the process they use, it seems to check out in spades. For me it gives entirely new face to entropy, that it comes from the net energy (surplus) that all macroscopic systems need to develop and operate at all times. http://www.synapse9.com/drafts/LawOfContinuity.pdf
Phil, I think your theorem of the divergence of individual events looks similar to the principle of maximum entropy. Say you don’t know the acceleration of an object but you know that it must possess some mean value. Then the accelerations following an exponential distribution will be a conservative approximation given the limited information at your disposal.
The light at the end of the tunnel is getting brighter when I’ll be able to get back to enjoyable stuff like this.
Have you caught any glimpse of the dual affine connection business of Amari yet? Here he relates the associated divergences to Renyi entropy.
They held what looked like a fascinating meeting on Information Geometry in Leipzig last Summer, at which Amari spoke.
“A nonlinear transformation of a divergence function or a convex function causes a conformal change of the dual geometrical structure. In this context, we can discuss the dual geometry derived from the Tsallis or Renyi entropy. It again gives the dually flat structure to the family of discrete probability distributions or of positive measures.”
From when I looked at these things, I remember enjoying Stochastic Reasoning, Free Energy, and Information Geometry.
Whoops, shouldn’t have used Markdown. As recompense, there’s a minus sign missing from equation 7 of the arXiv paper.
Thanks, David! I fixed your previous comment: it’s straight HTML on this blog, so you type this:
<a href = “http://www.math.ntnu.no/~stacey/Mathforge/Azimuth/”>Azimuth Forum</a>
to create a link like this:
Azimuth Forum
(I know you know this, but I want to keep telling everyone reading this blog how it works.)
Thanks for catching a missing sign! I’ve been catching lots of sign errors in my calculations.
Wow, a whole book on Stochastic Reasoning, Free Energy, and Information Geometry? I’ll have to look at it — if they don’t point out the connection between free energy and Rényi entropy, something is seriously amiss. The funny thing is that nobody I know has much intuition for Rényi entropy, while every physicist worth their salt has a deep understanding of free energy.
(Some people working on systems ecology and thermoeconomics seem to use “exergy” as a synonym for free energy. It’s a cute name, and it avoids confusion with the free energy of conspiracy theories — that is, energy that we could get for free, if only big business weren’t preventing us! But it’s a shame to have essentially the same concept studied by three communities under three different names: free energy, Rényi entropy and exergy.)
I think I’m sort of beginning to understand the “dual affine connections” business, and I’ll try to talk about that later in my series of posts on information geometry. So far I’ve been trying to understand the Fisher information metric from a bunch of different viewpoints; I think this is a good first step. In my latest post in that series, I reviewed relative entropy, so that next time I can prove the Fisher information metric is the Hessian of the relative entropy.
When you assume that a reader has not heard about Rényi entropy before, is there a tagline that explains why it is interesting and/or useful?
(I mean, the main blog post is about another way to think about Rényi entropy that could turn out to be useful, but what is the primary reason to think about it at all? Besides that it is additive.)
I have no idea why anyone else thinks Rényi entropy is interesting or useful! This is why I found myself annoyed to see papers discussing it without explaining what it means. And that’s why I was happy to discover that it’s really just a slight modification of the concept of free energy. Now I understand Rényi entropy and I know why it’s interesting and useful.
Well, I’m exaggerating slightly. I do understand a bit about why people care about these special cases of Rényi entropy:
•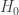 (the ‘max-entropy’)
(the ‘max-entropy’)
•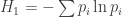 (the ‘Shannon entropy’, the really important one)
(the ‘Shannon entropy’, the really important one)
•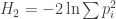 (the ‘collision entropy’)
(the ‘collision entropy’)
• (the ‘min-entropy’)
(the ‘min-entropy’)
For example, min-entropy and max-entropy show up if you ask an extreme pessimist or optimist how much work they can extract from a situation in which there’s some randomness (a ‘mixed state’). This paper gives a nice explanation:
• Oscar Dahlsten, Renato Renner, Elisabeth Rieper and Vlatko Vedral, On the work value of information.
This paper makes a nice attempt to understand Rényi entropy in general:
• Peter Harremöes, Interpretations of Renyi entropies and divergences.
It includes a history of this question!
But basically, I think Rényi entropy arose when Rényi studied the axiomatic derivations of the ordinary Shannon entropy and noticed that if you removed some axioms while keeping the crucial additivity axiom
where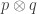 is the tensor product of probability distributions, you get a bunch of ‘generalized entropies’, which include the Rényi entropies.
is the tensor product of probability distributions, you get a bunch of ‘generalized entropies’, which include the Rényi entropies.
As you know, people like to do that. Someone gets a good idea: other people generalize it.
So, the idea of Rényi entropy has been floating around at least 1960. And, some researchers on machine learning and statistical inference seem to find it useful:
• D. Erdogmuns and D. Xu, Rényi’s entropy, divergence and their nonparametric estimators, in Information Theoretic Learning: Rényi’s Entropy and Kernel Perspectives,
ed. J. Principe, Springer, 2010, pp. 47-102.
But don’t ask me why!
Tom Leinster may have more to say about why Rényi entropy is a natural measure of biodiversity — it’s used for that too.
Here’s an example of why I’m happy to see the relation between Rényi entropy and free energy. Free energy is additive, and this makes a lot of sense, physically. So the additivity of Rényi entropy makes sense to me now, because it’s just a temperature-dependent multiple of free energy.
One vague comment to be made is that the Rényi entropies interpolate in a natural way between the special cases you pointed out, just as spaces interpolate between
spaces interpolate between 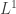 ,
, 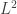 and
and 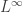 . I’ll be lazy and not bother to explain details myself, but add that if you want to fit Rényi entropies into a bigger mathematical picture, you should spend some time pondering generalized means.
. I’ll be lazy and not bother to explain details myself, but add that if you want to fit Rényi entropies into a bigger mathematical picture, you should spend some time pondering generalized means.
Since I’ve spent some time understanding Tom’s work on biodiversity, I can say something about that, too. Say the probabilities are the relative sizes of populations of distinct species in a community. (“Species” may refer to taxonomical species, or some other way of grouping organisms; likewise sizes may be measures of the number of individuals, or biomass, or something else.) If you want to measure how diverse the community is, one idea you might have is this: randomly pick an individual and say how “typical” that individual’s species is in the community. The more typical an average individual is, the less diverse the community.
are the relative sizes of populations of distinct species in a community. (“Species” may refer to taxonomical species, or some other way of grouping organisms; likewise sizes may be measures of the number of individuals, or biomass, or something else.) If you want to measure how diverse the community is, one idea you might have is this: randomly pick an individual and say how “typical” that individual’s species is in the community. The more typical an average individual is, the less diverse the community.
So how can you quantify the typicality of a species, given only the relative abundances ? The most obvious choice is to use
? The most obvious choice is to use  itself: the “typicality” of species
itself: the “typicality” of species  is precisely how common it is. This leads to
is precisely how common it is. This leads to  as a way to quantify how non-diverse the community is, so that
as a way to quantify how non-diverse the community is, so that 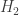 turns out to quantify how diverse the community is.
turns out to quantify how diverse the community is.
One could just as well, however, measure typicality by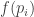 , where
, where ![f:[0,1] \to \mathbb{R}](https://s0.wp.com/latex.php?latex=f%3A%5B0%2C1%5D+%5Cto+%5Cmathbb%7BR%7D&bg=ffffff&fg=333333&s=0&c=20201002) is any increasing function. If
is any increasing function. If  and
and  , this leads to using
, this leads to using  as a reasonable way to measure diversity. (I leave as an exercise the justification of
as a reasonable way to measure diversity. (I leave as an exercise the justification of  as a measure of diversity for
as a measure of diversity for 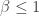 .) Using different values of
.) Using different values of  gives more or less influence to rare species, similar to what John said about
gives more or less influence to rare species, similar to what John said about 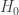 and
and 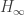 reflecting the viewpoints of extreme pessimists or optimists.
reflecting the viewpoints of extreme pessimists or optimists.
Mark wrote:
Indeed, when I started trying to understand the goofy-looking formula for Rényi entropy:
I was reminded of the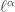 norm:
norm:
(which people usually call the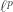 norm, but we’re getting too many
norm, but we’re getting too many  ‘s around here).
‘s around here).
But then I wondered: what’s so great about raising a probability to a power? As you note, for some applications any increasing function would work about equally well. Is the Rényi entropy just one of an enormous family of equally good (or bad) ideas, or is there really something special about it?
And then I remembered that in statistical mechanics, the probability of a system in equilibrium at temperature being in its
being in its  th state is:
th state is:
where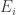 is the energy of the
is the energy of the  th state and
th state and  is Boltzmann’s constant. (We can set this constant to 1 by a wise choice of units, and theoretical physicists usually do, but I think I’ll leave it in for now.)
is Boltzmann’s constant. (We can set this constant to 1 by a wise choice of units, and theoretical physicists usually do, but I think I’ll leave it in for now.)
This makes it obvious what ‘raising probabilities to powers’ might mean:
You can think of this as:
• multiplying all the energies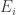 of our system by
of our system by 
or if you prefer:
• replacing the temperature by
by  ,
,
or for that matter:
• dividing Boltzmann’s constant by , which we’d do if we changed our units of either energy or temperature.
, which we’d do if we changed our units of either energy or temperature.
It doesn’t really matter which we do — they’re all just different ways of talking about the same thought. So let’s say we’re rescaling the temperature:
This led me to call the process
‘thermalization’. The idea is that as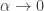 , we are turning up the temperature. Physicists all know that as the temperature increases, states of high energy become more likely to be occupied… and in the limit of infinite temperature, all allowed states become equally likely. And so, as
, we are turning up the temperature. Physicists all know that as the temperature increases, states of high energy become more likely to be occupied… and in the limit of infinite temperature, all allowed states become equally likely. And so, as  gets smaller,
gets smaller,  approaches 1, at least if it was nonzero in the first place.
approaches 1, at least if it was nonzero in the first place.
Conversely, as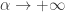 we are lowering the temperature. At low temperatures only the lowest-energy states have any significant chance of being occupied.
we are lowering the temperature. At low temperatures only the lowest-energy states have any significant chance of being occupied.
But of course when we thermalize a probability distribution
the result is no longer a probability distribution — the ‘s don’t sum to 1 — until we divide by a fudge factor.
‘s don’t sum to 1 — until we divide by a fudge factor.
But this fudge factor is famous in statistical mechanics: it’s the partition function! It’s a remarkably important quantity. Everything we might want to know about our system is encoded in it! This is quite remarkable, given that it starts life as a mere ‘fudge factor’, designed to correct a mistake.
I guess it’s a case of what Tom Leinster would call fudge power!
In particular, the logarithm of the partition function times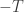 is the Helmholtz free energy: the amount of energy that’s not in the form of heat. And this logarithm explains the logarithm in the formula for Rényi entropy!
is the Helmholtz free energy: the amount of energy that’s not in the form of heat. And this logarithm explains the logarithm in the formula for Rényi entropy!
And then everything started falling into place.
But it’s still falling.
John B,
I don’t intend to seem too dense, but it looks to me that the formula for probability is already thermalized:
John F. wrote:
The formula for probabilities is just
We’re starting with a completely arbitrary probability distribution here: nothing to do with temperature, energy, etcetera.
The ‘thermalization’ trick starts by choosing an arbitrary number and finding real numbers
and finding real numbers 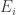 such that
such that
Such numbers always exist if , and then they’re always unique:
, and then they’re always unique:
Then, to thermalize the probability distribution we define
we define
where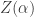 is chosen to make the new probabilities sum to 1:
is chosen to make the new probabilities sum to 1:
We now have a new probability distribution depending on , namely
, namely  .
.
Rényi entropy is a funny -dependent entropy that reduces to the usual Shannon entropy when
-dependent entropy that reduces to the usual Shannon entropy when 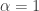 . To understand Rényi entropy, I claim we need to understand the process of thermalizing a probability distribution.
. To understand Rényi entropy, I claim we need to understand the process of thermalizing a probability distribution.
And here’s one way:
If we think of the original probabilities as the thermal equilibrium state of some physical system at temperature
as the thermal equilibrium state of some physical system at temperature  , the new
, the new  ‘s can be thought of as the result of:
‘s can be thought of as the result of:
• multiplying all the energies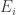 of our system by
of our system by 
or:
• replacing the temperature by
by  ,
,
or:
• dividing Boltzmann’s constant by , which we’d do if we changed our units of either energy or temperature.
, which we’d do if we changed our units of either energy or temperature.
John,
This is kind of out there, but I wonder if the thermalization factor as you defined it can predict deviations from the Einstein relation. I have looked at characterization of charged transport in disordered semiconductors and the curves always show an Einstein relation greater than kT/q. I have thought it had something to do with a highly smeared density of states, where the fundamental relation goes as N/(dN/dE), but you may be on to a unifying explanation.
Transport in disordered material typically shows a power-law response tail and this links back to non-extensive entropy such as Tsallis and Renyi. Is it possible that the carriers are somehow “thermalized” away from equilibrium and this is what could cause a larger effective kT/q?
I am saying this is way out there because I have yet to find any paper that claims any deviation from the Einstein relation can exist.
The significant link to Azimuth is that these disordered semiconductor materials (amorphous Si:H, etc) are the primary material for making photo-voltaics. Of course there is a huge amount of practical interest surrounding this topic. That essentially explains my interest in the math and physics, as you have to really go out on a limb to hit on a breakthrough.
WebHubTel wrote:
Unfortunately I don’t understand what you’re talking about it! It sounds interesting, but I don’t even know what the “Einstein relation” is, much less anything about disordered semiconductors. I can learn stuff if you’re willing to explain it slowly.
Hmm. I haven’t yet understood the stuff people keep muttering off in the distance about Tsallis entropy and power laws.
By the way, the Tsallis entropy is non-extensive but “convex” (it behaves as you’d hope when taking mixtures of states), while the Rényi entropy is “extensive” (when you set two uncorrelated systems side by side, their entropies add) but nonconvex. Either one is a function of the other — so you can have your cake, and eat it too, but not in the same room.
Only in the special case where the Rényi entropy reduces to the Boltzmann-Gibbs-Shannon-von Neumann entropy do you get something that’s both extensive and convex.
Interesting. Is there some practical use for deviations from the Einstein relation (whatever that is)?
(staying on the same indentation level)
About the Einstein relation: it is the ratio between the diffusivity and mobility coefficient of a charged particle or any particle moving under some force. In one sense it gives an idea of how strong random walk fluctuations are in comparison to forced movements. It is usually derived under equilibrium conditions.
I cared (somewhat tangentially) about Rényi entropies a few years ago, because they’re related to the distribution of node degrees in random spatial networks. See Eqs. (12) through (16) in Herrmann et al. (2003), “Connectivity Distribution of Spatial Networks” Phys. Rev. E 68: 026128, arXiv:cond-mat/0302544.
Basically, if you build a graph by throwing vertices randomly into a box and drawing edges between those which land close to each other, the moments of the resulting graph’s degree distribution will be given by the Rényi entropies of the probability function according to which the vertices were deposited. (There’s a caveat about going to the thermodynamic limit, and the formula also brings in the Stirling numbers of the second kind.)
And on the subject of “throwing things into a box”, I’m aware of an application some people cooked up to use Rényi entropies in nuclear physics, to estimate the thermodynamic entropy of something whose phase-space properties are known from a limited number of samples. In this case, the “box” is a discretized phase space, and the trick is to calculate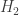 and
and  from what you’ve measured, after which you extrapolate down to
from what you’ve measured, after which you extrapolate down to 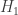 . See A. Bialas and W. Czyz (2000), “Event by event analysis and entropy of multiparticle systems”, Phys Rev D 61: 074021, arXiv:hep-ph/9909209; also A. Bialas and K. Zalewski, arXiv:hep-ph/0602059.
. See A. Bialas and W. Czyz (2000), “Event by event analysis and entropy of multiparticle systems”, Phys Rev D 61: 074021, arXiv:hep-ph/9909209; also A. Bialas and K. Zalewski, arXiv:hep-ph/0602059.
Thanks for all the helpful information, Blake!
In a more mundane way, the collision entropy
shows up when you throw rocks into boxes, with each rock landing in the i th box with probability pi, and the result of each throw being independent from the rest. Then
is the probability that two chosen rocks land in the same box.
Hmm. I guess the Rényi entropies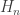 for
for 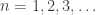 all have interpretations of this sort… and now that I think about it, I bet you’re talking about the same idea!
all have interpretations of this sort… and now that I think about it, I bet you’re talking about the same idea!
Yes — in the one case, “land in the same box” means “be in the same phase-space bin”, while in the other, it means “fall close to each other in Euclidean space”.
I’ve been thinking about all this again in the context of trying to invent final-exam problems for my statistical-physics course (it’ll be a take-home exam…), and I noticed something I believe I missed before. This bit in the “Rényi entropy and free energy” paper caught my attention:
This seems to be doing the same thing, morally speaking, as Eq. (20) in Bialas and Czyz (arXiv:hep-ph/9909209).
They do a polynomial extrapolation of the sequence down to
down to 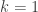 , which sounds like another way of saying to take the collection of secant lines and extrapolate to what the tangent line should be.
, which sounds like another way of saying to take the collection of secant lines and extrapolate to what the tangent line should be.
This is also reminiscent of something I found while playing around with higher-order generalizations of mutual information, where a binomial transform also arose … but that’s getting beyond the scope even of a take-home exam.
By the way, in response to Tim’s question, I should add:
It may seem a bizarre and unproductive research strategy to study concepts precisely because nobody has explained why they’re important, or what they really mean. But for a long time, I’ve spent a fraction of my time on this slightly decadent approach, as kind of hobby.
It can actually turn up interesting results. For example, after decades of struggling to understand the octonions — a quirky algebraic gadget that fills everyone who meets it with a mixture of curiosity and revulsion — it eventually became clear that classical superstring theory Lagrangians exist only in 3, 4, 6, and 10 dimensions precisely because the 4 normed division algebras allow the construction of Lie super-2-groups extending the super-Poincaré group in these dimensions… with the 10-dimensional, physically interesting case arising from the octonions!
So, when I heard David Corfield start talking about generalized entropies like Tsallis entropy and Rényi entropy, my instinctive repugnance upon meeting concepts that seemed like ‘generalization for the sake of generalization’ was mixed with a desire to understand why anyone cared about them, and to fit them into the framework of ideas I already understood.
I have drastically rewritten my paper based on the comments here, especially those by Blake Stacey, Eric Downes, and ‘tomate’.
I also had a new idea of my own. I’m calling the Rényi entropy instead of
instead of  now, because the Rényi entropy is almost the q-derivative of free energy! This is cool because q-derivatives show up when we q-deform existing mathematical structures (like groups) to get new ones (like quantum groups). It’s now clear that the Rényi entropy is a q-deformed version of the ordinary entropy.
now, because the Rényi entropy is almost the q-derivative of free energy! This is cool because q-derivatives show up when we q-deform existing mathematical structures (like groups) to get new ones (like quantum groups). It’s now clear that the Rényi entropy is a q-deformed version of the ordinary entropy.
The new version is here:
• Rényi entropy and free energy.
The idea is now to take an arbitrary probability distribution and write it as the state of thermal equilibrium for some physical system at some chosen temperature
and write it as the state of thermal equilibrium for some physical system at some chosen temperature 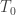 . Let
. Let  be the free energy of this system at an arbitrary temperature
be the free energy of this system at an arbitrary temperature  .
.
By definition, the Rényi entropy of the probability distribution is
is
But Eric Downes noted that
where is a temperature with
is a temperature with
Thanks to this formula, the Rényi entropy is revealed to have a simple physical meaning. This was pointed out by ‘tomate’.
Start with a physical system in thermal equilibrium at some temperature. What is its Rényi entropy? To find out, ‘quench’ the system, suddenly dividing the temperature by .
.
Then:
The formula
can be written as follows:
The q-derivative of a function is defined by
is defined by
So, it’s clear that — except for some small stuff that’s explained in the paper — the Rényi entropy is essentially a q-derivative of free energy.
As , the q-derivative reduces to an ordinary derivative, and the Rényi entropy reduces to the ordinary Shannon entropy.
, the q-derivative reduces to an ordinary derivative, and the Rényi entropy reduces to the ordinary Shannon entropy.
I don’t know what the connection between Rényi and q-deformation really means, but it suggests there’s a bigger picture lurking in the background.
I saw the revised paper go up on the arXiv earlier today — thank you very much for mentioning my comment!
And, now I know what the q in q-deformation stands for: quenching! (-:
Sure — thanks for spotting those references and maybe alerting Eric Downes to this stuff!
I’m not sure I have the guts to mention in this paper that q stands for “quenching” — but I’d definitely use that line in a talk.
For now, I’m happy just to be able to use the word quench in a paper. It’s so incredibly macho.
I think there’s a missing “tr” in the equation in between (7) and (8). The Rényi entropy at temperature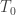 should be
should be
Thanks – fixed! You can see an ever-improving version of the paper on my website.
Another, smaller point (or pair of them): in the graf beginning “After the author noticed this result”, the name “Schlogl” should be “Schlögl”.
Ööf! What a pun!
Thanks — fixed!
John,
You may be interested in a more general form of entropy that generalizes Tsallis/Renyi entropies to a functional parameter given in this paper by Jan Naudts. See section 4 for the definitions of the generalized logarithms and entropies.
These guys are related to generalized versions of Fisher Information, gradient systems, machine learning, evolutionary game theory, and more.
Hay, this looks like fun. Can I play? Whad’ya know, Renyi entropy also shows up in non-equilibrium statistical dynamics. I’ve written up a quick note explaining this:
Trajectory divergences in non-equilibrium statistical dynamics
Fascinating paper! You sure know a lot of different entropy-related concepts. I’m just catching up…
Here’s a little idea on how to view entropy as a functor. Let’s define to two monoidal categories, call them and
and  , such that Shannon and Rényi entropies are (strict) monoidal functors
, such that Shannon and Rényi entropies are (strict) monoidal functors 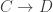 . An object of
. An object of  is defined to be a finite set together with a probability distribution. A morphism of
is defined to be a finite set together with a probability distribution. A morphism of  is defined to be a function which is compatible with the probabilities in the obvious way. (Such a function is necessarily surjective.) For
is defined to be a function which is compatible with the probabilities in the obvious way. (Such a function is necessarily surjective.) For  , we take the poset of non-negative real numbers in the reversed order. The monoidal structure on
, we take the poset of non-negative real numbers in the reversed order. The monoidal structure on  is given by cartesian products of sets and forming the product of the probability distributions. On
is given by cartesian products of sets and forming the product of the probability distributions. On  , it is simply the addition of real numbers.
, it is simply the addition of real numbers.
Then what is a strict monoidal functor from to
to  ? It assigns to each probability distribution
? It assigns to each probability distribution  a non-negative number
a non-negative number 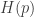 such that:
such that:
(1) it is invariant under permutations,
(2) it is non-increasing under the operation of grouping some outcomes to a single one;
(3) it satisfies additivity for independent distributions.
The Rényi entropies have all of these properties; as does any positive linear combination of Rényi entropies. So, are there any other strict monoidal functors from to
to  besides these? Has this categorical point of view been written down anywhere?
besides these? Has this categorical point of view been written down anywhere?
I wonder if Censov’s (or Chensov’s) work bears on this. It was mentioned here, and here. Frank Hansen writes:
[3] N.N. Censov, Statistical Decision Rules and Optimal Inferences, Transl. Math. Monogr., volume 53. Amer. Math. Soc., Providence, 1982.
Interesting question. And it’s also interesting that any such functor H induces a functor from (categories enriched in C) to (metric spaces).
I think you’re missing one small thing. In the definition of C, you say that morphisms are functions “compatible with the probabilities in the obvious way”, which I take to mean measure-preserving. This does not imply that the function is surjective. Rather, it implies that the complement of the image has measure 0. So when you refer in condition (2) to “the operation of grouping some outcomes to a single one”, the term “some” must include the possibility of “none”. In other words, (2) means not only
but also
(which together imply that the last inequality is actually an equality). But that’s fine: all the Rényi entropies satisfy this further condition.
It strikes me that you don’t have a continuity condition anywhere, and continuity often appears in axiomatizations of entropy. But perhaps you can get it for free.
Have you seen Rényi’s original paper?
Your conditions are satisfied not only by the Rényi entropies of order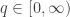 , but in fact by those of order
, but in fact by those of order ![q \in [-\infty, \infty]](https://s0.wp.com/latex.php?latex=q+%5Cin+%5B-%5Cinfty%2C+%5Cinfty%5D&bg=ffffff&fg=333333&s=0&c=20201002) (hence positive linear combinations of these). So if the answer to your first question (“are there any other…?”) is to be “no”, then you’d better include that full range of
(hence positive linear combinations of these). So if the answer to your first question (“are there any other…?”) is to be “no”, then you’d better include that full range of  s.
s.
When doing entropy of negative order, one has to be a bit careful about zero probabilities. Thus, for ,
,
Also
and as usual
(In the last expression, it makes no difference whether the maximum ranges over all or only those for which
or only those for which  .)
.)
Anyway, it would be really nice if your hunch turned out to be right. Among other things, it would provide a nice companion to these two theorems.
Actually, the above conjecture is not quite right, for essentially trivial reasons. There are certain linear inequalities between the for different values of
for different values of  . Taking for example
. Taking for example  , it is clear that
, it is clear that  also is a monoidal functor from C to D! Assuming that there are no linear dependencies between Rényi entropies, this shows that there are other such functors which are not *positive* linear combinations or integrals of Rényi entropies.
also is a monoidal functor from C to D! Assuming that there are no linear dependencies between Rényi entropies, this shows that there are other such functors which are not *positive* linear combinations or integrals of Rényi entropies.
It still remains unclear (to me at least) whether there are any such functors which lie outside the (closed) linear hull of Rényi entropies, but I bet that the answer is yes…
I agree that (indeed,
(indeed,  is decreasing in
is decreasing in  ). But is it so clear that
). But is it so clear that  is monoidal? E.g. is it clear that
is monoidal? E.g. is it clear that  decreases when you group some outcomes to a single one? I haven’t tried to calculate it, but I don’t see why it should be true at first glance.
decreases when you group some outcomes to a single one? I haven’t tried to calculate it, but I don’t see why it should be true at first glance.
Ah, you’re right, it’s not clear that the difference is functorial. It might have been too late last night…
One more thing: when you speak of “positive linear combinations” of Rényi entropies, you’re going to need to allow infinite linear combinations, i.e. integrals.
So in summary, I think a plausible form of your (implicit) conjecture is something like this: every strict monoidal functor H from C to D is of the form
where is a finite positive Borel measure on
is a finite positive Borel measure on ![[-\infty, \infty]](https://s0.wp.com/latex.php?latex=%5B-%5Cinfty%2C+%5Cinfty%5D&bg=ffffff&fg=333333&s=0&c=20201002) . (This integral does make sense: for each p, the integrand is continuous and bounded.)
. (This integral does make sense: for each p, the integrand is continuous and bounded.)
Hi, Tobias! That’s a beautiful idea—I haven’t seen it expressed in categorical language like that before! If Tom Leinster hasn’t seen it before, it must be new. And thanks, Tom, for making it even more beautiful!
I read your comments when I woke up last night and couldn’t get back to sleep because my head was whirring with thoughts. Someone had told me an amazing relationship between special relativity and the fact that planets have elliptic, parabolic or hyperbolic orbits in the inverse square force law, and I was trying to figure out what it meant. But your comments made my insomnia even worse. I came up with some interesting ideas. Alas, they seem to have developed some flaws in the clear light of day. But they still seem worth mentioning.
Tobias conjectured a way to characterize all positive linear combinations of Rényi entropies. It might be even nicer to characterize the Rényi entropies themselves.
Tobias’ proposed characterization is in terms of symmetric monoidal functors. The main idea behind the adjective ‘symmetric monoidal’ here is that the entropy of a product of finite probability measure spaces is the sum of the entropies of the individual spaces:
So, is sort of analogous to a homomorphism of abelian groups (or even better, commutative monoids).
is sort of analogous to a homomorphism of abelian groups (or even better, commutative monoids).
Now, a linear combination of abelian group homomorphisms is again an abelian group homomorphism. That’s why Tobias’ idea can’t characterize only Rényi entropies; positive linear combinations of Rényi entropies also work. But linear combinations of ring homomorphisms are not again ring homomorphisms. So, let’s try to think of Rényi entropies as something more like ring homomorphisms.
Right now they carry multiplication to addition:
This is a bit awkward, so let’s take the exponential of entropy—and just for now, let’s call it extropy. The name here is a joke, but the idea has been advocated by David Ellerman here on this blog, and by Tom Leinster elsewhere.
So, for any Rényi entropy , let
, let
Now we have
and we can hope that extends to something like a ring homomorphism, by also obeying
extends to something like a ring homomorphism, by also obeying
But what is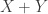 ? For this I think it’s best to switch from finite probability measure spaces to finite measure spaces. After all, if we have two measure spaces
? For this I think it’s best to switch from finite probability measure spaces to finite measure spaces. After all, if we have two measure spaces  and
and  , their disjoint union
, their disjoint union 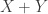 becomes a measure space in an obvious way—but if
becomes a measure space in an obvious way—but if  and
and  have total measure 1,
have total measure 1, 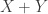 will have total measure 2. We could try tricks to get around this, but I don’t feel like it.
will have total measure 2. We could try tricks to get around this, but I don’t feel like it.
So, let be the category of finite measure spaces. This is a bit like a ring. More precisely, it’s a ‘rig category’ with
be the category of finite measure spaces. This is a bit like a ring. More precisely, it’s a ‘rig category’ with 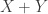 and
and  defined in the obvious ways.
defined in the obvious ways.
Let be the set of nonnegative real numbers made into a category with a unique morphism
be the set of nonnegative real numbers made into a category with a unique morphism 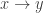 whenever
whenever 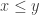 . This becomes a rig category with
. This becomes a rig category with 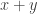 and
and 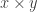 defined in the usual way.
defined in the usual way.
So, now we can ask: what are the rig functors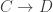 ?
?
But then comes a surprise, I think…
Maybe I’ll leave this question as a puzzle before trying to regroup and march on:
Puzzle. Do the Rényi extropies define rig functors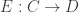 ? Can you completely classify such functors?
? Can you completely classify such functors?
By the way, I’m so pleased with this stuff right now that I feel we should write a joint paper on it. I start more papers than I finish, but…
I have the feeling that I’m missing the point here… but I’ll give it a go.
The exponential of the Rényi entropy of order q is , defined by
, defined by
for finite probability distributions p. Here I’m assuming ; the other values of
; the other values of ![q \in [-\infty, \infty]](https://s0.wp.com/latex.php?latex=q+%5Cin+%5B-%5Cinfty%2C+%5Cinfty%5D&bg=ffffff&fg=333333&s=0&c=20201002) are handled in the usual way.
are handled in the usual way.
I don’t know the definition of the Rényi entropy of a finite measure space. One could of course normalize the measure space to become a probability space and take its entropy, but that might not be the right thing to do.
Anyway, if is to preserve +, then for any sequence
is to preserve +, then for any sequence 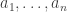 of nonnegative reals, we must have
of nonnegative reals, we must have
where on the right-hand side,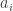 denotes the measure space consisting of a single point with measure
denotes the measure space consisting of a single point with measure 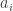 . Whatever the Rényi extropy of a measure space is, it seems unlikely that it satisfies such a formula. In fact, I reckon I could prove it’s impossible: for if we take the
. Whatever the Rényi extropy of a measure space is, it seems unlikely that it satisfies such a formula. In fact, I reckon I could prove it’s impossible: for if we take the 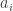 s to add up to 1 then we know what the left-hand side is, and it surely can’t be decomposed as a sum of functions of the
s to add up to 1 then we know what the left-hand side is, and it surely can’t be decomposed as a sum of functions of the 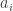 s.
s.
So, John asks, what are the (strict) rig functors ? Well, by the displayed formula above, such functors are entirely determined by what they do to singleton measure spaces. This determines a function
? Well, by the displayed formula above, such functors are entirely determined by what they do to singleton measure spaces. This determines a function  from
from 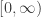 to
to 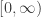 . Multiplicativity gives
. Multiplicativity gives
and functoriality gives
The “obvious” solutions to the functional equations and
and 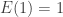 are those of the form
are those of the form  where t is a real constant. There are also non-obvious solutions, at least assuming the axiom of choice, but I suspect the subadditivity property of E excludes those. It also implies that
where t is a real constant. There are also non-obvious solutions, at least assuming the axiom of choice, but I suspect the subadditivity property of E excludes those. It also implies that 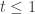 . (If
. (If 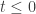 then we interpret
then we interpret  as 0.) So then,
as 0.) So then,
where![t \in (-\infty, 1]](https://s0.wp.com/latex.php?latex=t+%5Cin+%28-%5Cinfty%2C+1%5D&bg=ffffff&fg=333333&s=0&c=20201002) . These are all rig functors from C to D, and I suspect they’re the only ones.
. These are all rig functors from C to D, and I suspect they’re the only ones.
By the way, I assume that when you wrote “a unique morphism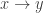 whenever
whenever 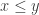 ” in your definition of D, you meant the opposite inequality. (That’s what Tobias had.) If not, I guess we get
” in your definition of D, you meant the opposite inequality. (That’s what Tobias had.) If not, I guess we get 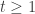 instead of
instead of 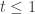 .
.
Tom wrote:
Yeah, I meant whatever he meant. But in fact, right now for a minute I feel like only including isomorphisms in my category ! So I’ll take the ‘core’ of the category
! So I’ll take the ‘core’ of the category  we had before: I’ll throw out all the morphisms except isomorphisms. I’ll call the core
we had before: I’ll throw out all the morphisms except isomorphisms. I’ll call the core 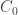 .
.
Then I believe all the strict rig functors
are of the form
where now can be any real number. This is the answer I was wanting you to get.
can be any real number. This is the answer I was wanting you to get.
Of course, when I first got this answer I was bummed out, because this isn’t the Rényi entropy. But I quickly recovered, because this is something even more important than the Rényi entropy: it’s the partition function!
The logarithm of the partition function is also famous: it’s called the free energy. So this sends in
in  to
to  in
in  , sort of like entropy does.
, sort of like entropy does.
And the Rényi entropy is a q-deformed derivative of the partition function, as explained in the paper this blog entry is about.
So all these important concepts show up in an interlocked way when we start thinking about functors from (or its core) to
(or its core) to  !
!
Ah, I see. Question: how do you exclude the “non-obvious” solutions to the functional equations ,
, 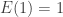 ? As you know, if we assume the axiom of choice then it’s possible to construct solutions not of the form
? As you know, if we assume the axiom of choice then it’s possible to construct solutions not of the form  .
.
Some extra hypothesis on E is needed in order to exclude these. A long list of possibilities is known: continuity, order-preservation, measurability, …
But maybe you want to leave that little niggle for another day and think about the bigger picture.
I don’t mind treating and
and  as categories internal to Top and assuming all our functors are continuous. In fact I felt the urge to do this for some other aspect of the problem, which I’ll try to tackle here after some sleep!
as categories internal to Top and assuming all our functors are continuous. In fact I felt the urge to do this for some other aspect of the problem, which I’ll try to tackle here after some sleep!
OK, sounds good.
Is there any reason not to treat and
and  as just rigs in Top? (Here
as just rigs in Top? (Here  is the rig of isomorphism classes of finite measure spaces.) If we’re not using any of the non-invertible maps in C then it seems to me that we might as well do this.
is the rig of isomorphism classes of finite measure spaces.) If we’re not using any of the non-invertible maps in C then it seems to me that we might as well do this.
Tom wrote:
I don’t know yet. But I’d hate to say that as soon as a category becomes a groupoid you might as well decategorify it and make it into a set—what would Ronnie Brown say? And Tobias’ results seem to use the whole structure of in a nice way. So it seems we should be trying to classify functors
in a nice way. So it seems we should be trying to classify functors  with various nice properties, including extending to functors
with various nice properties, including extending to functors  . (This is just a property here: such extensions are unique if they exist.) It seems that when we do, we’ll find many of the famous concepts from probability theory and statistical mechanics.
. (This is just a property here: such extensions are unique if they exist.) It seems that when we do, we’ll find many of the famous concepts from probability theory and statistical mechanics.
David C.’s point is also good: it’s wise to consider several variants of hand in hand: finite measure spaces, finite probability measure spaces, and maybe even finite sub-probability measure spaces. It’d be good to have a version such that ‘normalizing’ a measure and making it into a probability measure becomes a functor. Rényi entropy for probability measures is nicely understood starting from the free energy of measures whose normalizations are those probability measures.
hand in hand: finite measure spaces, finite probability measure spaces, and maybe even finite sub-probability measure spaces. It’d be good to have a version such that ‘normalizing’ a measure and making it into a probability measure becomes a functor. Rényi entropy for probability measures is nicely understood starting from the free energy of measures whose normalizations are those probability measures.
I have some more coherent remarks to make, but not now—I’ve been commandeered to get up and explore some neighborhoods in Singapore we haven’t been to yet, and that sounds like a great idea!
David, Tom, John: thanks for your feedback! Very intriguing food for thought! And sorry for being a bit slow in replying — a couple of papers on the drawing board are crying for attention…
@David: That could be an interesting connection! I will go to the library later and check out Censov’s stuff. What confuses me, though, is that entropy is not monotone under Markov morphisms: it increases under randomization, but decreases under coarse-graining.
@Tom: wow, I had not thought about categories *enriched* over C! Very cool, by “base change” entropy maps every such category into a Lawvere metric space. So, what is a category enriched over C? Ignoring technicalities about cardinality, it’s just an ordinary category together with a probability measure on each hom-set. This is a ‘random morphism’! There is a compatibility condition which requires the following: for any h:X–>Z and any other object Y, the probability P(h) equals the sum over all P(g)*P(f) where the composition of f:X–>Y and g:Y–>Z equals h. For example when the category is a finite group, this gives the normalized counting measure as the unique possibility. I wonder whether such probability measures always exist on a (say, finite) category, and how unique they are? Is there any relation to your work on Euler characteristics of categories?
Then, yes, you got me there, one should take care of stuff with measure 0.
About continuity, I would indeed hope that this comes out for free. Presently, I am confident that it is at least enough to assume continuity of the binary entropy around (1,0). For then one can consider various coarse-grainings of the product of a distribution p=(p_1,…,p_n) with the distribution (1-\epsilon,\epsilon) which give a distribution close to p with entropy close H(p). Without having worked out the details yet, I guess that this implies continuity.
@John: I agree that exponentiated entropy or ‘extropy’ is nicer than entropy itself. Counting a number of states is more natural than specifying it in terms of ‘bits’ or ‘nats’, isn’t it?
However when dropping the normalization and going from probability spaces to measure spaces, we loose functoriality of the entropy! In the original category C, functoriality means that the entropy decreases under coarse-grainings. But if we take a probability space and include it as a subset of a measure space, then the entropy increases! So, we cannot choose the orientation on the poset of real numbers in a way consistent with functoriality… But still, the idea of rig homomorphism seems something to keep in mind.
In any case, I would be very happy to write a joint paper about this! It strucks me as surprising that this seems to be new. I will put down an outline in LaTeX over the next few days and email it to all of you, ok?
Great; I look forward to seeing where this goes.
Regarding enrichment in C, I’m going to guess that not every finite category can be equipped with such a probability measure, and that when such measures do exist they needn’t be unique. But I don’t think that makes the picture any less nice.
Regarding relation to Euler characteristic: yes, I think there’s something there. Suppose you have a monoidal category C and you have some notion of the “size” of objects of C. Then there arises, in an automatic way, a notion of “size” (or magnitude, or Euler characteristic) for categories enriched in C.
Here, we know what the size of an object of C is: it’s the exponential of Shannon entropy. (At least, that’s the most obvious choice; you could try Rényi too.) So you get a notion of the size of a “probabilistic” category, i.e. a category enriched in C.
No time to say more for now, but can explain at more length if anyone wants. (And might explain at more length even if no one wants.)
Tobias wrote:
I’m assuming that if it’s new to Tom, who has thought a lot about entropies and likes category theory, it’s new.
Great. I wrote some material today and put it here. It doesn’t go too far, but at least it sketches how to start with a rig functor and get the Rényi entropy. I’m hoping that this will be helpful somehow.
Dangerous. I wouldn’t trust myself on that.
It might be worth having a look at this 1984 preprint of Lawvere. I haven’t read it myself. A thorough literature search would also include the work of Giry and Lawvere on the interaction of category theory and probability theory. Again, I haven’t read that stuff. This is why you shouldn’t rely on my knowledge of the literature :-)
Excellent! I am still waiting to find a few spare hours in which to write a page or two about this.
Lawvere’s paper looks like it might actually contain these ideas. Haven’t read it yet, though.
Some more food for thought:
(1) The “basic inequalities” of information theory are the following, expressed in terms of joint Shannon entropy:
• positivity of entropy,
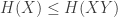


• positivity of conditional entropy,
• positivity of mutual information,
• positivity of conditional mutual information,
By the requirement that the entropy should be a monoidal functor, one obtains a categorical explanation/proof of the first two properties. (The second follows from considering the morphism ‘take the marginal’ from the joint distribution to the distribution of
to the distribution of  .)
.)
So now the question is: is there a categorical interpretation of the latter two properties? The third one looks a lot like Shannon entropy would be a lax monoidal functor, doesn’t it? And what about the fourth one?
(2) In information-theoretic terms, the intuition is to think of Shannon entropy as a sort of cardinality. Does that mean that Shannon entropy is somehow a decategorification, analogous to like the natural numbers are a decategorification of the category of finite sets? Is there a construction for monoidal categories which generalizes Shannon’s idea of considering many copies of a morphism and using this to define invariants (entropy and channel capacity)?
BTW, I still haven’t figured out how to use LaTeX on this blog and don’t want to bother the elves every time I post something. Are there any instructions available?
You just put ‘$latex’, then a space, then your LaTeX, then ‘$’.
There are further tips on maths in WordPress here and here.
I fixed up the LaTeX on your most recent post, Tobias. As David noted, I just needed to replace all expressions like this:
$H(X)$
with expressions like this:
$latex H(X)$
The space is crucial.
And don’t use double dollar signs: they don’t work.
John, I edited your nLab page to add some new material. (I’m saying this here in case anyone, such as Tobias, wants to take a look.)
Tobias wrote:
I don’t see him mentioning Shannon entropy or Rényi entropy. He seems to be talking about entropy, not from the viewpoint of statistical mechanics (where you start from a set of probability measures and write down a formula for the entropy of such a measure), but from the viewpoint of axiomatic thermodynamics (where you posit entropy as a function on some unspecified set or usually manifold, and impose axioms on it).
Since I’m not very knowledgeable about axiomatic thermodynamics, and Lawvere is doing his usual thing of pushing the subject he’s talking about to new heights of abstraction, it would take me a while to extract useful information from this paper.
Tobias wrote:
Something like that is true. The big difference is that unlike sets, which form a rig category, probability measure spaces have a natural product but not a natural coproduct. This is why I like measure spaces. I am trying to push the viewpoint that ‘the’ decategorification of the category of finite measure spaces is not the entropy or even the exponential of entropy, but the partition function.
The idea is to start with any finite set equipped with a measure
equipped with a measure  whose only set of measure zero is the empty set.
whose only set of measure zero is the empty set.
We can always write as some function
as some function
times counting measure, where
is some function called the energy.
Then we can think of as sitting inside a 1-parameter family of measures given by
as sitting inside a 1-parameter family of measures given by
times counting measure, where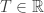 is called the temperature.
is called the temperature.
Then the partition function of the original finite measure space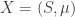 is
is
I’ve suppressed the variable on the left side;
on the left side; 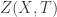 would be more accurate but it’s annoyingly long. The partition function obeys
would be more accurate but it’s annoyingly long. The partition function obeys
as we’d expect from a decategorification.
Moreover, as I told you here, we can recover the original finite measure space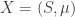 up to isomorphism from its partition function! So, we may call the partition function the decategorification of the category of finite measure spaces (whose only set of measure zero is the empty set).
up to isomorphism from its partition function! So, we may call the partition function the decategorification of the category of finite measure spaces (whose only set of measure zero is the empty set).
If you don’t like the parenthetical remark you can allow infinite energies and say . However, in my writeup of our work so far, I’ve been disallowing nonempty sets of measure zero. This is a small detail which can be fine-tuned later to maximize overall elegance.
. However, in my writeup of our work so far, I’ve been disallowing nonempty sets of measure zero. This is a small detail which can be fine-tuned later to maximize overall elegance.
By the way: this writeup asks what you and Tom think about certain ideas, e.g. whether you can understand them and if you like them! I’d appreciate some comments.
Also: your last comment has a lot of great ideas in it, but too many for me to process. Being a slow pedestrian sort, I would like at first to focus on your original goal of characterizing Rényi entropy as a functor!
Since Rényi entropy is a kind of -derivative of the logarithm of the partition function, it contains almost all the same information as the partition function. And for the same reason, I’m hoping my category-theoretic treatment of the partition function will connect nicely to a category-theoretic treatment of the e Rényi entropy! So, I’m hoping my writeup so far, which focuses on the partition function, is not really a huge digression from your original goal. However, I am still confused about why we’d want to take a perfectly nice rig homomorphism and then take the
-derivative of the logarithm of the partition function, it contains almost all the same information as the partition function. And for the same reason, I’m hoping my category-theoretic treatment of the partition function will connect nicely to a category-theoretic treatment of the e Rényi entropy! So, I’m hoping my writeup so far, which focuses on the partition function, is not really a huge digression from your original goal. However, I am still confused about why we’d want to take a perfectly nice rig homomorphism and then take the  -derivative of its logarithm!
-derivative of its logarithm!
Now, some things Tom wrote suggest that while probability measure spaces don’t have coproduct, we can still take two of them, say and
and  , together two numbers
, together two numbers ![x,y \in [0,1]](https://s0.wp.com/latex.php?latex=x%2Cy+%5Cin+%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) that sum to 1, and form a probability measure space I’ll call
that sum to 1, and form a probability measure space I’ll call  , where we multiply the probability measure on
, where we multiply the probability measure on  by
by  , and that on
, and that on  by
by  . More generally we can do this for
. More generally we can do this for  probability measure space using a point on the
probability measure space using a point on the  -simplex. I think there’s some way to formalize this using operads, which I forget.
-simplex. I think there’s some way to formalize this using operads, which I forget.
But, it could be that this extra structure explains why we want to take the -derivative of the logarithm of the partition function, and think of that as our favorite invariant of a probability measure space! Anyone have any good ideas?
-derivative of the logarithm of the partition function, and think of that as our favorite invariant of a probability measure space! Anyone have any good ideas?
Yikes, all this interesting stuff. I’m struggling to keep up.
Two quick points. One: in conversations with Mark Meckes, I’ve learned the important lesson that there’s no such thing as the entropy of a probability measure. It’s really the entropy of one probability measure relative to another. We’re misled by the fact that in the familiar examples, there’s a canonical reference measure: for finite sets, counting measure, and for , Lebesgue measure.
, Lebesgue measure.
Second point: there’s an operadic characterization of entropy. (I figured this out after some conversations with Steve Lack; as far as I know, it’s new.)
Take the operad whose space of n-ary operations is
whose space of n-ary operations is 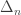 , the probability distributions on an n-element set. It’s a symmetric topological operad. We can consider its algebras in Cat(Top), the category of categories internal to Top. One such algebra is the topological monoid
, the probability distributions on an n-element set. It’s a symmetric topological operad. We can consider its algebras in Cat(Top), the category of categories internal to Top. One such algebra is the topological monoid  , regarded as a one-object topological category.
, regarded as a one-object topological category.
Now, given any operad P, there’s a notion of lax map between two P-algebras in Cat. In particular, you can consider lax maps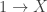 whose domain is the terminal category 1, where
whose domain is the terminal category 1, where  is a P-algebra in Cat. Let’s call such a thing a lax point of
is a P-algebra in Cat. Let’s call such a thing a lax point of  . (The concept of “monoid in a monoidal category” is an example of a lax point, when you take P to be the terminal operad; lax points aren’t just something invented for this purpose.)
. (The concept of “monoid in a monoidal category” is an example of a lax point, when you take P to be the terminal operad; lax points aren’t just something invented for this purpose.)
The theorem now is that the lax points of the -algebra
-algebra  are exactly the scalar multiples of Shannon entropy.
are exactly the scalar multiples of Shannon entropy.
I might try to say that in a less hurried way another time. I’ll also try to give you some feedback on what you wrote, John.
OK, I’ve got a better idea of what you’re doing now, John. I like the idea that the cardinality or decategorification is the entire partition function.
Here are a couple of semi-notational queries. First, you use temperature , but I’d understood previously that it’s better from a physics point of view to use inverse temperature
, but I’d understood previously that it’s better from a physics point of view to use inverse temperature 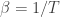 . It also seems to be more convenient from a purely mathematical point of view. Is there any reason why you’re sticking with
. It also seems to be more convenient from a purely mathematical point of view. Is there any reason why you’re sticking with  ? Or can we switch to
? Or can we switch to  ?
?
Second, is there a particular reason for working with the logarithm of , rather than
, rather than  itself? I mean, you put
itself? I mean, you put 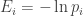 and
and
when you could instead just say
Or if we work with instead, that becomes the even simpler
instead, that becomes the even simpler
To me it seems easier to skip the s altogether and work directly with the
s altogether and work directly with the  s.
s.
If working with energies is just something so deeply ingrained in every physicist that it seems more natural that way, then fine, I can understand. But I’d like to find out whether there’s also a mathematical reason for doing so.
Tom wrote:
That’s fine; I’d love to wake up tomorrow and discover that you edited that page so you like it better.
If we use , I’ll need to explain that in physics applications it’s
, I’ll need to explain that in physics applications it’s 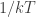 , where
, where  it Boltzmann’s constant and
it Boltzmann’s constant and  is temperature. But that’s fine; it just takes a sentence, and maybe all this ‘physical interpretation’ stuff belongs in its own separate section. For me it’s absolutely crucial, but for other readers it might be distracting or (worse) intimidating.
is temperature. But that’s fine; it just takes a sentence, and maybe all this ‘physical interpretation’ stuff belongs in its own separate section. For me it’s absolutely crucial, but for other readers it might be distracting or (worse) intimidating.
I guess that for me the idea of taking a probability and raising it to, say, the 1.7th power seemed very bizarre and unnatural until I had the revelation that led to my Rényi entropy paper.
I mean, I understood perfectly well when we might want to add probabilities, and when we might want to multiply them. So it made perfect sense to square a probability: if I have a 1/52 chance of drawing an ace of spades from a deck of cards, I have a 1/522 chance of drawing an ace of spades from each of two decks. But raising a probability to some noninteger power like 1.7?
Then I noticed that it’s a perfectly standard operation, but physicists call it ‘dividing the temperature by 1.7’, i.e. replacing
by
This is something they do all the time! I have an easy comfortable intuition for what it means to ‘chill out’ a physical system: improbable states become more improbable as it gets colder. So, all of a sudden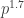 stopped looking so bizarre.
stopped looking so bizarre.
(There’s an important subtlety I’m skimming over here: when we take a probability distribution and raise all the probabilities to some power, we don’t get a probability distribution any more: we need to normalize the result! And this is what the physicists do.)
So anyway: go ahead and change
to
if you like. At some point I’ll need to add an explanation of ‘what the heck is really going on’, so that people who like physics can more deeply appreciate what we’re doing. But I’d need to do that no matter what! So, you might as well make the math as elegant as you can.
If you’d let me ‘borrow’ your result on Shannon entropy and operads, I might like to add that to this paper. (If you’re planning to publish it somewhere else, we can cite that). I bet it’s an important part of the overall story. There’s got to be some nice interpretation of Rényi entropy as a functor (say, valued in functions of ), and then an explanation of how this functor becomes ‘better’ when we restrict it to
), and then an explanation of how this functor becomes ‘better’ when we restrict it to  .
.
Regarding normalization, it often seems that there are reasons to keep three associated spaces under consideration when considering a space : the cone of finite measures, the truncated cone of subprobability measures, and the latter’s face of probability measures. The differential geometry of the Fisher-Rao metric applies to each.
: the cone of finite measures, the truncated cone of subprobability measures, and the latter’s face of probability measures. The differential geometry of the Fisher-Rao metric applies to each.
These three cropped up in our conversation here. There are certain advantages in not restricting to normalized measures, e.g., this one.
I always seem to be the one wanting an indexed category approach. We have a base category of sets, and fibred above each is the cone of finite measures. There are multiplication and sums of fibres ending up as fibres over products and disjoint union of sets, respectively.
I never can decide as to which morphisms to have in the base category: functions, relations, stochastic relations, conditional probability distributions. Then there would be interesting inducings going on between the fibres. And I guess the possibility of some hyperdoctrinal-type quantifier adjoints. We looked at this a little in the Progic thread.
Here’s something that you might find interesting in connection with entropy, John. Fact: the positive probability distributions on a finite set naturally form a real vector space.
I don’t know how well known this is, or how relevant it is to what we’re doing, but here goes. Let n be a positive integer. Write
and
The statement is that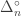 is naturally a real vector space. To say it briefly, it’s canonically isomorphic to
is naturally a real vector space. To say it briefly, it’s canonically isomorphic to 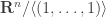 via the bijection
via the bijection 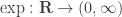 .
.
In more detail: exponential provides a bijection between and
and 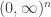 . Thus,
. Thus, 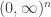 becomes a real vector space whose “zero” is
becomes a real vector space whose “zero” is  , whose “addition” is pointwise multiplication, and whose “scalar multiplication” assigns to a real number
, whose “addition” is pointwise multiplication, and whose “scalar multiplication” assigns to a real number  and a point
and a point 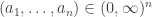 the point
the point 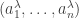 .
.
Now, the subspace of
of  corresponds to the subspace
corresponds to the subspace  of
of 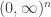 . The cosets of the subspace W are the rays
. The cosets of the subspace W are the rays  , where
, where  . (So our quotient is quite like the familiar quotient that gets you projective space.) Each such ray meets
. (So our quotient is quite like the familiar quotient that gets you projective space.) Each such ray meets  exactly once, so we can identify the quotient space
exactly once, so we can identify the quotient space  with
with 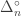 . This gives
. This gives 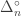 its vector space structure.
its vector space structure.
Explicitly, the vector space structure on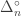 is as follows:
is as follows:
* The “zero” is .
.
* The “sum” of p and r is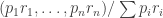 .
.
* “Scalar multiplication” takes a scalar and a point
and a point 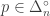 , and produces the point
, and produces the point 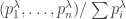 .
.
There’s a linear map given by
given by
It’s surjective, and its kernel is , so
, so  .
.
Hi, Tom! Thanks for all that. You’ll note that in my paper on Rényi entropy, I do what all physicists always do: I identify a strictly positive measure on a finite set
on a finite set  with a point
with a point  via
via
where is a positive constant we get to choose.
is a positive constant we get to choose.
Physicists call ‘temperature’ and
‘temperature’ and  ‘energy’ so that nonphysicists are scared to learn this useful trick.
‘energy’ so that nonphysicists are scared to learn this useful trick.
But you’re going further… I’ll have to think about what I can with that.
Hi John! You don’t scare me. Actually, I was well aware that the expressions coming up in my last comment look similar to the expressions appearing in your paper. That’s why I was hoping it might be helpful.
(There also seems to be some stuff about magnitude lurking in the background here. See Example 2.2.3(ii) of The magnitude of a metric space, if you feel like it.)
Did people here ever read Pavlov’s account of how to approach measure theory in a category theoretic way? John’s supervisor is involved.
Ugh, I did not know that theorem of Segal, nor the term “localized” measure space, but knowing that, and that these form an equivalent category to the W-star-algebras is certainly important.
As Mark Meckes wrote in a complementary answer over at mathoverflow, in probability theory the probability spaces are usually swept under the rug…
Tim wrote:
Of course you mean commutative W*-algebras.
Working with Segal forced me to read Integrals and Operators by Segal and Kunze, which explains the ‘algebraic’ approach to integration theory. But they don’t express things in terms of an equivalence of categories, since Segal didn’t like categories.
Here are some more thoughts, mainly for Tobias Fritz and Tom Leinster, but also for David Corfield and anyone else who is interested. I’ve been writing stuff on the nLab, but I need another burst of energy to overcome some obstacles, and maybe a bit more chatting here will help.
Tom mentioned that “the lax points of the -algebra
-algebra 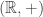 are exactly the scalar multiples of Shannon entropy”. While I still need to unravel that a bit, I figure that it should be pretty close to Fadeev’s theorem about Shannon entropy mentioned on the first page here:
are exactly the scalar multiples of Shannon entropy”. While I still need to unravel that a bit, I figure that it should be pretty close to Fadeev’s theorem about Shannon entropy mentioned on the first page here:
• Alfréd Rényi, Measures of information and entropy, in Proceedings of the 4th Berkeley Symposium on Mathematics, Statistics and Probability 1960, pp. 547–561.
But how close, exactly?
Let me state Fadeev’s theorem. I’ll modify the statement slightly to make it sound a bit more like a category theorist said it.
Here goes:
So, what’s the ‘magical property’? To state this, let’s write a probability measure on the set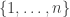 as an
as an  -tuple of numbers
-tuple of numbers ![p_i \in [0,1]](https://s0.wp.com/latex.php?latex=p_i+%5Cin+%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) with
with
Then the magical property is that
What’s the nice way to state this magic property using category theory?
How is this related to Tom’s result?
Fadeev’s result mentions continuity, Tom’s doesn’t. Oh, no – I think Tom’s result secretly does. Are your operads topological, Tom? I think so.
Fadeev’s ‘magical property’ seems to have something to with how is an operad: we’re taking a probability measure on a 2-point set and a probability measure on an
is an operad: we’re taking a probability measure on a 2-point set and a probability measure on an  -point set and ‘glomming them together’ and getting a probability measure on a
-point set and ‘glomming them together’ and getting a probability measure on a 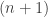 -point set.
-point set.
Okay, so now I’m guessing Tom’s result really is Fadeev’s theorem, stated in a slick way.
Am I on the right track, Tom?
Finding a categorical interpretation of the magical property is a fun puzzle! I think I can provide an answer.
As Tom has emphasized, it is often better to think in terms of relative entropy. So let’s try to take a category like FinMeas and assign entropies to the morphisms instead of the objects! Actually, let me revert to working with normalized measures, so that the category now is FinProb, finite probability spaces with measure-preserving functions. Optimally, we would expect to get a functor FinProb —> R, where now R is the abelian group of real numbers under addition, regarded as a category with one object. But that would be too good to be true, wouldn’t it?
But that is precisely what relative Shannon entropy is!! For an object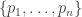 and a map
and a map ![f:[n]\rightarrow [m]](https://s0.wp.com/latex.php?latex=f%3A%5Bn%5D%5Crightarrow+%5Bm%5D&bg=ffffff&fg=333333&s=0&c=20201002) , the relative entropy is
, the relative entropy is
A simple calculation shows that this indeed maps composition of measure-preserving maps to sums of relative entropies. The magical property is the special case of this when we consider the object , the morphism which identifies the first two elements, and from there the morphism to the terminal one-element probability space.
, the morphism which identifies the first two elements, and from there the morphism to the terminal one-element probability space.
I hope that this makes sense. In fact, Lawvere’s paper deals with this kind of functor! So, it might be a good idea to try and understand that.
BTW, sorry for not being able to keep up with the pace here… I see new comments appear faster than I can read them, and the nlab page also has expanded at a frightening rate ;) And starting tomorrow I will be offline until Wednesday…
You are keeping up with the pace, Tobias! You answered my puzzle shortly after I asked it! We’re coming up with so much stuff, none of us feels like we’re keeping up with the other two.
I really like the idea of studying relative entropy as a functor, in the way you’ve described. You’ll have to give me until Wednesday to think about this. I can’t keep up with the pace!
Tobias, I don’t understand your formula for H(f). Maybe that’s because I don’t understand the set-up.
You say “for an object “. I guess this is an object of the category FinProb you’d just mentioned, i.e. a finite probability space. You also say “a map
“. I guess this is an object of the category FinProb you’d just mentioned, i.e. a finite probability space. You also say “a map ![f: [n] \to [m]](https://s0.wp.com/latex.php?latex=f%3A+%5Bn%5D+%5Cto+%5Bm%5D&bg=ffffff&fg=333333&s=0&c=20201002) “. Presumably
“. Presumably ![[n] = \{1, \ldots, n\}](https://s0.wp.com/latex.php?latex=%5Bn%5D+%3D+%5C%7B1%2C+%5Cldots%2C+n%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) , and
, and  is simply a map of finite sets. This gives a pushforward measure
is simply a map of finite sets. This gives a pushforward measure 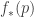 on
on ![[m]](https://s0.wp.com/latex.php?latex=%5Bm%5D&bg=ffffff&fg=333333&s=0&c=20201002) .
.
Now in the formula for H(f), we have a sum running over . Since there are terms
. Since there are terms  in the summation, I assume that
in the summation, I assume that  runs over
runs over ![[n]](https://s0.wp.com/latex.php?latex=%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) . But then there’s also a term
. But then there’s also a term 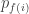 , which then doesn’t make sense. Maybe you mean
, which then doesn’t make sense. Maybe you mean 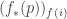 ? Applying the definition of pushforward measure, the formula then becomes
? Applying the definition of pushforward measure, the formula then becomes
That looks a bit unlikely, so I guess that’s not what you meant, and I’m puzzled.
I’m also puzzled because I’d understood relative entropy to be something that was defined for a pair of probability measures on the same (finite) set. How does that fit into your definition of the relative entropy of a map?
Are you, perhaps, taking a measure on
on ![[n]](https://s0.wp.com/latex.php?latex=%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) , another measure
, another measure  on
on ![[m]](https://s0.wp.com/latex.php?latex=%5Bm%5D&bg=ffffff&fg=333333&s=0&c=20201002) , and a map
, and a map ![f: [n] \to [m]](https://s0.wp.com/latex.php?latex=f%3A+%5Bn%5D+%5Cto+%5Bm%5D&bg=ffffff&fg=333333&s=0&c=20201002) of finite sets, and then considering the entropy of
of finite sets, and then considering the entropy of  relative to
relative to 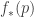 ?
?
Sorry for having been unclear on this. It may seem unlikely, but your guesses in your initial three paragraphs are correct.
You are right in reminding me that relative entropy refers to a situation with two probability measures on the same set. So it might be better to call this the ‘entropy of a map’. I would suggest to think of it as quantifying the information loss one incurs by applying the map.
Does this make sense to you?
I am currently working on writing this down on the nlab page. I hope that it’s not complete bogus :P
Hi, T&T!
I’m glad you’re writing more stuff on the nLab. I’ve been distracted by the Desargues graph
and its role in chemistry—you’ll see what I mean someday soon.
I too was confused by Tobias’ use of the term ‘relative entropy’, until I saw he was talking about some sort of entropy of a map instead of the usual notion.
One funny thing is that Rényi’s own characterization of Rényi entropies (Theorem 3 on page 55 here) uses the usual concept of relative entropy. So, one thing I want to do is understand that result better using more category theory! But what’s a nice way to think about the category of finite sets with two probability measures on them.
I will attempt to rejoin the fray as soon as I pull myself away from my current obsession.
Actually, my idea for finding a categorical interpretation of the ‘magical property’ is complete bogus, as I noticed while writing it out in detail on the nLab page.
If is measure-preserving, then my definition boils down to saying that
is measure-preserving, then my definition boils down to saying that
and then it is a triviality that is functorial! In particular, one can do precisely the same thing for Rényi entropy.
is functorial! In particular, one can do precisely the same thing for Rényi entropy.
When we start with some probability space , define
, define  to be
to be  with the first two elements identified, takes
with the first two elements identified, takes  to be the projection map from
to be the projection map from  to
to  , then we get
, then we get
and this corresponds to the remaining term in the magical property.
corresponds to the remaining term in the magical property.
However, what is missing is the identification of this third term as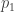 times a binary entropy!
times a binary entropy!
At some point I would like to understand the operadic formulation of the magical property. Is your (Tom’s) book the right place for doing that, given that I understand the basic ideas behind operads?
I erroneously used the term ‘relative entropy’ for the following reason: let’s consider two random variables and
and  , which are objects in the category. Then also the joint variable
, which are objects in the category. Then also the joint variable  is an object in the category, and we may consider the projection morphism
is an object in the category, and we may consider the projection morphism 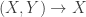 .
.
Then the entropy of this projection morphism is the relative entropy of given
given  . So the entropy of a map generalizes the concept of relative entropy.
. So the entropy of a map generalizes the concept of relative entropy.
Ah! Excellent.
Tobias wrote:
Did you look at the material Tom wrote on the nLab? It’s just a sketch, so we should fill in details. I’m not sure I understand every detail, but I feel sure I could. So, maybe you can ask some questions here and I’ll try to answer them by filling in details on the nLab.
Tobias, sorry, I missed your question about my book. No, I don’t think it’s the right place to get the background for that result on operads and entropy.
Off the top of my head I can’t think where the definition of lax map of algebras for an operad is written down. It’s essentially a special case of the notion of lax map of algebras for a 2-monad, but that doesn’t really help. What I should do at some point is simply write it out. The trouble is that it involves diagrams, which are a bit of a pain in this medium.
Tom: here’s what I’m confused about. The laxness of the map between algebras would seem to be a way to express an inequality, since there’s a morphism in , or
, or 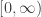 , whenever one number is greater than or equal to another. But none of Fadeev’s axioms for Shannon entropy involve inequalities!
, whenever one number is greater than or equal to another. But none of Fadeev’s axioms for Shannon entropy involve inequalities!
John: you’re confused because you’re treating as a poset, whereas I’m treating it as a monoid (viewed as a 1-object category). So a morphism in
as a poset, whereas I’m treating it as a monoid (viewed as a 1-object category). So a morphism in  is not an inequality: it’s a real number.
is not an inequality: it’s a real number.
Just when I was in the mood for typing up some diagrams (and that’s not common), the nLab seems to be down. So I latexed them instead. In fact, I did this operadic characterization of Shannon entropy in very nearly complete detail. It’s here.
Thanks, Tom! I have more to say, but I feel like carrying this conversation over to the n-Café, since it’s getting a bit heavy on the category theory, so people will enjoy it more there than here.
Just about to get on the train to the 92nd Peripatetic Seminar on Sheaves and Logic in Oxford — think of it like the Hogwarts Express — so will answer briefly. Yes, that result on “lax points” is a dressing-up of the (Fadeev) result in Rényi’s paper. Yes, my operads were topological. Yes, the magical property is about operadic composition (but stated a bit more economically).
If you unravel the definition of lax point, you find that there are three conditions: one on composition in the operad, one on the unit in the operad, and one on the symmetric group action. (And because everything’s in Top, you get continuity too.) The symmetry one is symmetry, and the unit one is redundant. But what I think is the cool part is that the composition one is essentially the magical property.
So, that’s how you can state the magical property using category theory.
(There are some other ways to state it using category theory; Steve Lack and I figured out a couple. But the one about lax points is the slickest formulation that I know of.)
I’ll type up the details if you don’t get there before me, but you can guess them anyway. If you know — or can guess — the definition of a lax map of algebras for a 2-monad, then you have everything you need to unravel my statement.
Hmm, so you and Tobias are proposing seemingly different explanations of the magical property! If they’re both correct, we have a bit of thinking to do. The nice thing about his is that it brings relative entropy into the game, which seems to be crucial for characterizing Rényi entropy — at least the way Rényi did it.
Have fun at the Hogwarts Academy of Sheaves and Logic!
Okay, next I want to take this paper:
• Alfréd Rényi, Measures of information and entropy, in Proceedings of the 4th Berkeley Symposium on Mathematics, Statistics and Probability 1960, pp. 547–561.
and try to translate his characterization of Rényi entropies into category-theoretic language. As with Fadeev’s characterization of Shannon entropy, I won’t entirely succeed. In fact this time I’ll succeed even less! But it’s worth trying…
Actually he gives two characterizations, Theorem 2 on page 553 and Theorem 3 on page 555. The first theorem is a bit unsatisfactory because it involves the function
which looks suspiciously like something you’d see in the definition of Rényi entropy. The second one is nicer but it characterizes the relative Rényi entropy of one probability measure with respect to another. Of course faithful readers of this blog know I consider relative entropy to be more fundamental than ‘plain old’ entropy. So, I should be happy. But it sounds like we may need a fancier category where an object consists of two probablity measures on the same finite set, and that’s slightly off-putting.
Anyway, let me try the first theorem. There’s another twist involved in this theorem: it’s not about probability measures on finite sets, it’s about what David calls ‘subprobability measures’, meaning nonnegative measures whose total mass is . Rényi calls them ‘generalized probability measures’, but I like David’s term better.
. Rényi calls them ‘generalized probability measures’, but I like David’s term better.
Suppose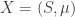 is a finite subprobability measure space, meaning that
is a finite subprobability measure space, meaning that  is a finite set and
is a finite set and  is a nonnegative measure on
is a nonnegative measure on  such that
such that
is . And suppose
. And suppose 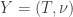 is another finite subprobability measure space. Then the disjoint union of
is another finite subprobability measure space. Then the disjoint union of  and
and  gets a subprobability measure on it iff
gets a subprobability measure on it iff
and when this happens, we’ll call the resulting subprobability measure space . It’s annoying that this
. It’s annoying that this  operation is only partially defined, but let’s soldier on…
operation is only partially defined, but let’s soldier on…
Here is that function I mentioned!
is that function I mentioned!
So: can we make this more pretty?
Opportunities abound, because it’s so darn ugly. Condition 1) is beautiful, condition 2) is a dumb little normalization condition, and condition 3) is the 800-pound gorilla that needs to be trained and beautified.
For what it’s worth, the ‘total mass function’
is a rig functor:
and it’s also continuous. I know what all continuous rig functors from to
to  are, in case that helps.
are, in case that helps.
And for what it’s worth, the functions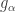 are all the continuous functions from
are all the continuous functions from  to
to 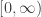 that send addition to multiplication and obey some other tiny property.
that send addition to multiplication and obey some other tiny property.
So, there’s a lot of stuff about addition and multiplication being preserved, or one getting changed to the other, going on here!
John Baez’ recent relation between free energy and Rényi entropy is a nice potential competitor for the efficient calculation of free energy differences […]
Tsallis entropy is a close relative of Rényi entropy, which I discussed here earlier. Just as Rényi entropy is a kind of q-derivative of the free energy, the Tsallis entropy is a kind of q-derivative of the partition function […]
[…] actually be experimentally measured in real systems. I was finally inspired to write this up due to John Baez, who recently discussed the significance of Renyi entropy to equilbrium statistical […]
[…] I have written about Rényi entropy and its role in thermodynamics before on this blog. I’ll also talk about it later in this conference, and I’ll show you my slides. […]
[…] so we’re continuing some conversations about entropy that we started last year, back when the Entropy Club was active. But now Jamie Vicary and Brendan Fong are involved […]