A Characterization of Entropy

Over at the n-Category Café some of us have been trying an experiment: writing a math paper in full public view, both on that blog and on its associated wiki: the nLab. One great thing about doing things this way is that people can easily chip in with helpful suggestions. It’s also more fun! Both these tend to speed the process.

Like Frankenstein’s monster, our paper’s main result was initially jolted into life by huge blasts of power: in this case, not lightning but category theory. It was awesome to behold, but too scary for this blog.

First Tom Leinster realized that the concept of entropy fell out — unexpectedly, but very naturally — from considerations involving ‘operads’, which are collections of abstract operations. He was looking at a particular operad where the operations are ‘convex linear combinations’, and he discovered that this operad has entropy lurking in its heart. Then Tobias Fritz figured out a nice way to state Tom’s result without mentioning operads. By now we’ve taught the monster table manners, found it shoes that fit, and it’s ready for polite society:

• John Baez, Tobias Fritz and Tom Leinster, A characterization of entropy in terms of information loss, Entropy 13 (2011), 1945–1957.

The idea goes like this. Say you’ve got a finite set X with a probability measure p on it, meaning a number 0 \le p_i \le 1 for each point i \in X, obeying

\sum_{i \in X} p_i = 1

Then the Shannon entropy of p is defined by

S(p) = - \sum_{i \in X} p_i \, \ln(p_i)

This funny-looking formula can be justified in many ways. Our new way involves focusing not on entropy itself, but on changes in entropy. This makes sense for lots of reasons. For example, in physics we don’t usually measure entropy directly. Instead, we measure changes in entropy, using the fact that a system at temperature T absorbing a tiny amount of heat \Delta Q in a reversible way will experience an entropy change of \Delta Q / T. But our real reason for focusing on changes in entropy is that it gives a really slick theorem.

Suppose we have two finite sets with probability measures, say (X,p) and (Y,q). Then we define a morphism f: (X,p) \to (Y,q) to be a measure-preserving function: in other words, one for which the probability q_j of any point in Y is the sum of the probabilities p_i of the points in X with f(i) = j.

A morphism of this sort is a deterministic process that carries one random situation to another. For example, if I have a random integer between -10 and 10, chosen according to some probability distribution, and I square it, I get a random integer between 0 and 100. A process of this sort always decreases the entropy: given any morphism f: (X,p) \to (Y,q), we have

S(q) \le S(p)

Since the second law of thermodynamics says that entropy always increases, this may seem counterintuitive or even paradoxical! But there’s no paradox here. It makes more intuitive sense if you think of entropy as information, and the function f as some kind of data processing that doesn’t introduce any additional randomness. Such a process can only decrease the amount of information. For example, squaring the number -5 gives the same answer as squaring 5, so if I tell you “this number squared is 25”, I’m giving you less information than if I said “this number is -5”.

For this reason, we call the difference S(p) - S(q) the information loss of the morphism f : (X,p) \to (Y,q). And here’s our characterization of Shannon entropy in terms of information loss:

First, let’s write a morphism f: (X,p) \to (Y,q) as f : p \to q for short. Suppose F is a function that assigns to any such morphism a number F(f) \in [0,\infty), which we think of as its information loss. And suppose that F obeys three axioms:

1) Functoriality. Whenever we can compose morphisms f and g, we demand that

F(f \circ g) = F(f) + F(g)

In other words: when we do a process consisting of two stages, the amount of information lost in the whole process is the sum of the amounts lost in each stage!

2) Convex linearity. Suppose we have two finite sets equipped with probability measures, say p and q, and a real number \lambda \in [0, 1]. Then there is a probability measure \lambda p \oplus (1 - \lambda) q on the disjoint union of the two sets, obtained by weighting the two measures by \lambda and 1 - \lambda, respectively. Similarly, given morphisms f: p \to p' and g: q \to q' there is an obvious morphism from \lambda p \oplus (1 - \lambda) q to \lambda p' \oplus (1 - \lambda) q'. Let’s call this morphism \lambda f \oplus (1 - \lambda) g. We demand that

F(\lambda f \oplus (1 - \lambda) g) = \lambda F(f) + (1 - \lambda) F(g)

In other words: if we flip a probability-λ coin to decide whether to do one process or another, the information lost is λ times the information lost by the first process plus (1 – λ) times the information lost by the second!

3) Continuity. The same function between finite sets can be thought of as a measure-preserving map in different ways, by changing the measures on these sets. In this situation the quantity F(f) should depend continuously on the measures in question.

In other words: if we slightly change what we do a process to, the information it loses changes only slightly.

Then we conclude that there exists a constant c \ge 0 such that for any morphism f: (X,p) \to (Y,q), we have

F(f) = c(S(p) - S(q))

In other words: the information loss is some multiple of the change in Shannon entropy!

What’s pleasing about this theorem is that the three axioms are pretty natural, and it’s hard to see the formula

S(p) = - \sum_{i \in X} p_i \, \ln(p_i)

hiding in them… but it’s actually there.

(We also prove a version of this theorem for Tsallis entropy, in case you care. This obeys a mutant version of axiom 2, namely:

F(\lambda f \oplus (1 - \lambda) g) = \lambda^\alpha F(f) + (1 - \lambda)^\alpha F(g)

where \alpha is a parameter with 0 < \alpha< \infty. Tsallis entropy is a close relative of Rényi entropy, which I discussed here earlier. Just as Rényi entropy is a kind of q-derivative of the free energy, the Tsallis entropy is a q-derivative of the partition function. I’m not sure either of them are really important, but when you’re trying to uniquely characterize Shannon entropy, it’s nice for it to have some competitors to fight against, and these are certainly the main two. Both of them depend on a parameter and reduce to the Shannon entropy at a certain value of that parameter.)

This entry was posted on Thursday, June 2nd, 2011 at 10:48 am and is filed under information and entropy, probability. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.

32 Responses to A Characterization of Entropy

  1. Tom Leinster says:
    2 June, 2011 at 11:28 am

    Here’s a photo showing all three of us (with theorem).

    Reply
    • John Baez says:
      2 June, 2011 at 11:37 am

      And here’s a photo taken when you actually first proved the theorem:

      Reply
    • Phil Henshaw says:
      3 June, 2011 at 1:29 am

      I wish I could do justice to the math, but where one deals with natural systems there’s a need for information gain prior to information loss, as organizations of matter/energy can’d decay before they develop.

      So one then needs to have a fraction of the energy that becomes unusable for system output having been consumed in building the system first. You can trace some of these actual energy flows and processes, of course, so it’s not really a matter of theory. That’s where I need to define some more variables and add layers of complication to the standard model of entropy, though. So, you might call the energy cost for building and maintaining the system “entropy-A” and the energy cost of running the system “entropy-B”.

      Would these two kinds of entropy losses, for creating and running a system, have convenient correlaries for your information theory model of entropy? It seems there should be, as information involves information gain before loss too, I think typically. That would seem to imply two types of information entropy also then, or only when discussion information that is organized?

      Reply
  2. DavidTweed says:
    2 June, 2011 at 12:21 pm

    As someone who’s horribly applied, I tend to think of entropy as the “equal utility consequences” case of more involved utility+probability (e.g., where the utility, or importance, function is identically 1). I guess in that case the functoriality axiom is different, which is how that case escapes the theorem of being just the Shannon entropy; looks like the other two axioms still apply.

    Reply
    • John Baez says:
      2 June, 2011 at 1:20 pm

      What’s the formula for that more involved thing given a probability distribution p: X \to [0,1] on a finite set X together with utility function u: X \to [0,\infty) (or whatever the right range of ‘utilities’ is)?

      I’m wondering if this is something I know (in disguise), and whether our theorem generalizes in this direction. There are various directions I want to generalize it in…

      Reply
    • Tom Leinster says:
      2 June, 2011 at 1:32 pm

      David, I’d like to know about that too. I’m interested in entropy as an index of biodiversity, and sometimes – cold-hearted as it may seem – people like to put a value on each species. Which area of “horribly applied” mathematics does this come from?

      Reply
    • DavidTweed says:
      5 June, 2011 at 4:42 pm

      (I’m spending time on trains and looking for new accommodation, so apologies for slow pace of responses.)

      In response to Tom, when I say “horribly applied” what I mean is I’m tasked to “tackle” problem X and to a large degree need to do something with that problem even if that involves less than elegant approaches. One concrete example is what’s known in robotics as Simultaneous Localization And Mapping (SLAM) (link without maths). The idea is that — unless someone gives you a map — both humans and, more importantly, robots explore new areas by estimating up a map of the area, but that also involves estimating where you are on this new map (since almost nothing can “dead reckon” position perfectly). Now you can view the “map” as a huge probability distribution of “things (walls, etc) and their positions” conditioned on “sensor and odometer readings”. (Being real measurements all readings generally have an error, which can be viewed as probabilistic, on them.) Not only is this a complicated probability distribution with uncertainty (so it makes sense to talk about the entropy of the “map” at a given time), but this is an “active” situation in that the robot generally has a choice where to go next, which will affect what it’s next sensor readings “is a reading of” (if you see what I mean).

      So one way to make the choice is to move to a position where, based on the current probability distribution “map” and the range of conceivable (ie, consistent with the current distribution) sensor readings, choose the one which on average decreases the entropy by the most. Now all this is perfectly consistent with Shannon entropy and KL divergence. However, suppose the robot is doing SLAM (building the map) for a reason, eg, to escape a building, it may be that there’s an additional expectation about where an exit is supposed to be. It’s clearly a good general idea to reduce the entropy of the map/your position in it, but it may turn out to be better to further nail down a reasonably well explored area of the map (medium entropy reduction) where you think the exit is rather than go into an unexplored area of the map (big entropy reduction) where you don’t think the exit is. (In some situations you could completely discard the regions where you know the exit isn’t, but in a more general case you generally aren’t sure enough to completely discard things from the problem instance as irrelevant, you just want to focus on more likely areas.) Then this situation is an example where

      1. the Shannon entropy exactly captures the degree to which a given revealed result would be “surprising” but

      2. not all results that are part of the “probabilistic distribution” of variables connected with a problem have a _task relevance_ equal to their _surprisingness_.

      This kind of thing shows up in lots of areas.

      As mentioned Shanon et al are considering the perfectly valid, and quite common case, where all the information is equally “relevant”/”important”. However, sometimes that’s not the case. The mathematics isn’t as elegant or well-developed, but I’ll try and write down some of the things people use in other areas in a later comment.

      Reply
  3. Tobias Fritz says:
    2 June, 2011 at 8:05 pm

    Very nice post, John! It is indeed quite remarkable how the initial highly abstract monstrous formulation has been tamed into a well-behaved pet. We should do the same with quantum Frankenstein!

    Reply
    • John Baez says:
      3 June, 2011 at 2:07 am

      Let’s start now! Here’s a first question: which class of completely positive maps has the entropy-decreasing property analogous to that of the measure-preserving functions f: X \to Y that are so important in our first paper? Clearly maps coming from unitary operators do, but we need some non-invertible ones too.

      I’m looking around for helpful references, and I happened to notice that page 6 of this paper does the quantum version of a trick you invented in the classical case! It extends the definition of von Neumann entropy H from density matrices to arbitrary nonnegative matrices A, via:

      H(A) = \mathrm{Tr}(\eta(A)) - \eta(\mathrm{Tr}(A))

      where

      \eta(x) = - x \ln x

      This should be very familiar to you, Tobias. And in equation 4 he notes that

      H(\lambda A) = \lambda H(A)

      which is just our homogeneity condition.

      Inequality 6 looks like our so-called ‘magic equation’, but it’s an inequality. Hmm, I wonder if this screws things up. No, I don’t think so, because the operators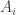 A_i here are all operators on the same Hilbert space, while in the quantum version of the magic inequality they’d be operators on different Hilbert spaces.

      This paper is also somewhat interesting: it’s called “Entropic characterization of quantum operations”, which is a promising title; it doesn’t seem to answer my question above, but it does have some interesting remarks about quantum Rényi entropy and also “map entropy” and “minimum output entropy”, which seem to be two ways of assigning entropies to completely positive operators.

      Reply
    • Tobias Fritz says:
      3 June, 2011 at 7:34 am

      It’s interesting to see that other people have come up with the same definition of the entropy of a general measure! So then there ought to be some sense to it.

      You’re asking what the quantum analogue of a measure-preserving function between finite probability spaces would be. First of all, we might ask ourselves, what is the quantum analogue of a function between finite sets? To see what this could be, recall Gelfand’s theorem:

      “The category of compact Hausdorff spaces is contravariantly equivalent to the category of unital C*-algebras.”

      In particular, the category of finite sets is contravariantly equivalent to the category of finite-dimensional commutative C*-algebras. This basically means that any finite-dimensional commutative C*-algebra is isomorphic to some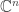 \mathbb{C}^n with componentwise multiplication.

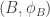      So, a quantum finite probability space should be a finite-dimensional C*-algebra A together with a C*-algebraic state \phi:A\rightarrow\mathbb{C}. A measure-preserving function from (A,\phi_A) to (B,\phi_B) should be a *-homomorphism f:B\rightarrow A (note the ‘wrong’ direction!) which is compatible with the states in the obvious way. The hope is that entropy should be monotonically decreasing under all of these morphisms, but then I’m not sure how to prove this at the moment (I don’t even know the right definition of entropy here, see below).

      Then the direct sum of C*-algebras extends the disjoint union of sets, and by this we can also make sense of “convex combinations” of quantum finite probability spaces.

      But how would we define the entropy of a C*-algebraic state \phi:A\rightarrow\mathbb{C}? After all, von Neumann entropy is usually defined for density matrices, isn’t it? There are two things to say here: the first is the classification of finite-dimensional C*-algebras: these are all direct sums of matrix algebras,

      M_{n_1}(\mathbb{C})\oplus\ldots\oplus M_{n_k}(\mathbb{C})

      And in the case of the C*-algebra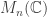 M_n(\mathbb{C}), there is a bijective correspondence between C*-algebraic states and density matrices as follows:

      \phi(a)= \mathrm{Tr}(\rho a)\quad\forall a\in A

      Okay, this might be a start. I have to run to the airport now…

      Reply
      • John Baez says:
        5 June, 2011 at 11:00 am

        Tobias wrote:

        Okay, this might be a start.

        Yes, that’s a very good start!

        But on second thought, since we’ll be doing lots of heavy-duty math that’s not very related to the environmental thrust of this blog, let’s continue this discussion over here, at the n-Category Café. I’ve tried to push your thoughts forward a bit.

        Reply
  4. David Corfield says:
    3 June, 2011 at 8:10 am

    Does anyone over at this blog understand what entropy and cocycles have to do with each other conceptually? We didn’t get to the bottom of Ebanks’ comment here.

    Reply
    • John Baez says:
      3 June, 2011 at 8:17 am

      I asked Tobias to summarize the various facts you and he turned up in your conversation about entropy and cocycles. I also mentioned what cocycles are always good for: building mathematical ‘layer cakes’. I suspect that by taking any cocycles you found, and using them to do what cocycles are always good for, something nice will happen. But I was feeling a bit overworked, so I was trying to get him (or maybe you) to help assemble the puzzle pieces.

      Reply
    • David Corfield says:
      3 June, 2011 at 8:55 am

      I missed that. And I see Tobias replied. Perhaps best to continue over there.

      Reply
  5. Don Foster says:
    4 June, 2011 at 11:25 pm

    I cannot judge if the mathematics are solid, but the conclusion that there is a negative correlation between entropy and information is suspect in my view.
    Perhaps it depends on which side of the looking glass you are calculating, whether you are dealing with information itself or just its shadows on the wall, whether you are dealing with probabilities or particulars.
    In a “real” dynamic, information is an actual player, a determiner of outcome. Its signal is a change in the state of energy, a measurable event.
    Can one, in a nutshell, characterize entropy by the notion that when energy is asked to turn (change state), not all of in makes the corner? Is information thereby increased or diminished? Does one count the actual states or simply use a statistical measure?
    I suppose the real question is whether this argument has any trace of traction for you. Regards.

    Reply
    • John Baez says:
      5 June, 2011 at 2:32 am

      I didn’t mean to suggest that information was negatively correlated to entropy; they’re essentially synonyms in this subject. Physical processes never map two different states to the same state, but mathematical processes can—I mentioned the example of squaring a number—and such processes can decrease the amount of information.

      I don’t really get your argument; entropy is a slippery subject so I only feel comfortable when I can mentally see the calculations that are implicitly lurking behind a verbal argument.

      Reply
      • Web Hub Tel says:
        5 June, 2011 at 5:02 am

        I think I can see what Don means, but I will put my own twist on it. Take the case of noise, and something like 1/f noise to be specific. Do we measure the entropy in the time domain, say of the autocorrelation function of the noise? Or do we measure the entropy in the frequency domain, which may be more in line with idea of a mean energy according to quantization levels. In other words, does the entropy change dependent on how we measure the probability of the occupied state space?

        I am trying to place it in Don’s terms that we may be looking at something from opposite sides of the looking glass. He used the term shadow — which one of these, time domain or frequency domain, is just an entropy shadow of the other one?

        Reply
      • Don Foster says:
        5 June, 2011 at 3:22 pm

        John, thanks, I am on tippy-toe here, perhaps out of my depth.
        I cannot give you a well-formed equation, but I don’t believe we should equate the entropy of a signal with its information. The former does not fully circumscribe the latter.
        Shannon entropy is a kind of volumetric, a measure of a signal’s irreducibility. While it is an index of proven utility to communication engineers, it does not a fully characterize the nature of information.
        Entropy is a measure of disjunction where as, in a more wholesome scheme of things, information would be functionally consistent with correlation at various radii of influence.
        This leaves us with the perhaps unpalatable proposition that information is the very quantity that is extracted as redundancy by Shannon’s measure.
        Whether this is some dusty heresy, long set aside, or simple misapprehension, I am unable to determine.

        Reply
        • Don Foster says:
          5 June, 2011 at 5:58 pm

          By way of illustration, or perhaps to simply dig a deeper hole, consider this prosy paradox. At least it is familiarly biological.
          We have a symbol set of 7,120 distinct symbols arrived at in the following manner.
          The distance between pitcher’s mound and home plate is 60.5 feet. If we consider a hemisphere of that radius and divide its entire surface into strike zone sized areas, we would find they number 7,120 and we assign a unique symbol to each one.
          Now the pitcher is on the mound and he is having a very good day. He is throwing perfect strikes, one after the other.
          An analysis by Shannon’s H theorem of the black box signal being produced by the pitcher’s efforts would find the repetition of one symbol, that identifying the actual strike zone, and hence calculate some minimal information in the signal.
          On the other hand, a pitcher who was throwing perfectly at random (but at least keeping it off the ground) would produce a signal found to have maximal information content.
          Furthermore, consider that a five-ounce baseball moving at 90 mph has the kinetic energy equivalent to 10^22 electron volts. Here we measure in electron volts because that is the unit of energy transferred in the interaction of single photon with chlorophyll antenna and throwing baseballs is a biological activity arising from photosynthesis.
          So the singularly directed energy of the baseball represents the confluence of a vast biochemical watershed, 10^22 disparate energy impulses brought together and organized into a single vector.
          Despite the accumulated improbability, the perfect pitcher is producing, by Shannon’s measure, a signal of minimal information content.

        • Web Hub Tel says:
          6 June, 2011 at 3:12 am

          Don, I would say that your example has a few too many constraints. For a given baseball pitcher, all those biological mechanisms are working in concert and use energy to accomplish a task. The example is also censored in that the pitchers are self-selected from a population that know how to pitch. I also would think that a pitcher throwing at random would exhibit maximum information entropy, but then again what is he basing his randomness decision on — the spin of a wheel?

        • Phil Henshaw says:
          6 June, 2011 at 1:26 pm

          Don, I think you’re getting caught by the difficulty that “information” theory has almost nothing whatever to do with the “meaningfulness” of the evidence at hand.

          I think you might just as well call it “disinformation theory” as a measure of the variety of messages one might read into a given collection of data (like the maximum confusion you might have about what the story is). I think the ultimate subject of information theory is how to design automated communication machines for “passing notes in class” that can only be interpreted in one and only one way, for the least cost.

  6. Don Foster says:
    7 June, 2011 at 4:05 pm

    Phil, thanks. And yes, I believe Weaver warns that their H theorem does not deal with “meaning” on about the first page of his little book. Perhaps this is equivalent to statistical entropy being a path independent measure.
    The baseball example was meant to show that while the Shannon entropy of the black box signal (the pitcher throwing perfect strikes) recorded low information content, the internal energetic process of the black box, the greater metabolism of the pitcher, was in fact highly negentropic, far from a normal distribution. (This is not saying that it contravenes the second law, clearly a greater portion of energy goes to ground in the process) At this point I am not sure what that proves, but I am unsatisfied with the notion of an identity between information and entropy.
    The H theorem is a measure with a particular angle of incidence that, like a conic section, reveals one aspect of information but not the whole.
    Of course the genus of information theoretic measures is a living testament to evolution, there are new species at every turn. I have a middling grasp of the Shannon’s more fundamental theorems and it is likely that, unbeknownst to me, there is formal recognition that information is related to, but not identical to entropy.
    And, having come this far, unfortunately there is more. I regret being both flatfootedly declarative and perhaps ultimately unclear, but for me this is a germinal notion. Perhaps it is the season for a shift of paradigms and perhaps I am actually coming late to this understanding.
    Would things sort out more satisfactorily if we shift information upward in the cosmological hierarchy, grant it a more prominent, costarring role in nature’s grand opera?
    I have come to view it in this way. Information is energy’s counterpoise and correspondent constraint. Information keeps energy from running directly off the page, gives it pause and time to doodle things like planets and plants. Path is emergent in the interaction of energy and information and path is the salient feature in life process. And information theoretic measures lend themselves to the understanding of path.
    That’s probably more than enough. Regards.

    Reply
  7. Weekly Picks « Mathblogging.org — the Blog says:
    8 June, 2011 at 3:06 am

    Last but not least, Azimuth described the experiment of writing a paper on a blog. […]

    Reply
  8. Quora says:
    11 June, 2011 at 6:28 am

    Why would you multiply a function back by its natural log? Or do something in the form of [x ln(x)] / [y ln(y)]?…

    One reason would be in order to measure entropy, so x or y has to be a probability. -xlnx is then the entropy. Or, I should say entropy is the negative sum over all your possible x’s of that value. So if the random variable X can equal 0 (tails) or 1 …

    Reply
  9. Ady says:
    26 November, 2011 at 2:22 pm

    “A process of this sort always decreases the entropy”

    If the amount of information is decreased then the missing information is increased, so shouldn’t the entropy have increased? (It’s supposed to be a measure of the missing information – our ignorance about the system).

    Reply
    • Tobias Fritz says:
      27 November, 2011 at 12:53 pm

      There might be several ways to answer this question. Here’s my take on it.

      John wrote:

      It makes more intuitive sense if you think of entropy as information, and the function f as some kind of data processing that doesn’t introduce any additional randomness. Such a process can only decrease the amount of information. For example, squaring the number -5 gives the same answer as squaring 5, so if I tell you “this number squared is 25″, I’m giving you less information than if I said “this number is -5″.

      In my understanding, what John means by “information” is the amount by which your “missing information” changes when he tells you something about his number. Think of it as the amount of information contained in his message to you.

      Now consider the following two cases:

      If he tells you the number itself, your missing information suddenly decreases from total ignorance of the value of the number to complete knowledge of the number.

      On the other hand, if the tells you only the square of the number, your missing information will not decrease to 0, since you won’t know the sign of the number. Your missing information decreases by a smaller amount than in the previous case.

      The difference between these two cases is precisely our “information loss”.

      Reply
    • John Baez says:
      27 November, 2011 at 11:59 pm

      Tobias wrote:

      In my understanding, what John means by “information” is the amount by which your “missing information” changes when he tells you something about his number. Think of it as the amount of information contained in his message to you.

      Yes. It’s very easy to get mixed up about minus signs when studying entropy and information. I won’t be ultra-precise here because it seems that Ady and you and I all understand and agree about what’s going on.

      The entropy of a probability distribution is the expected amount of information you gain when you learn the value of a random variable distributed according to that probability distribution.

      So, it’s the expected amount of information you gain when someone sends you a message telling you the value of that random variable.

      Or, you could say it’s the amount of information you’re missing, before you know that random variable.

      Since I’ve thought about this a lot and have become pretty relaxed about it, I don’t mind saying ‘entropy is information’. But that can be confusing if you haven’t thought about this subject a lot.

      It’s a bit like how the sign of ‘work’ in physics can get very confusing if you don’t keep track of whether you mean ‘work done on the system’ or ‘work the system has done’.

      Reply
  10. More Second Laws of Thermodynamics « Azimuth says:
    24 August, 2012 at 2:14 pm

    […] By the way, Nielsen’s paper contains another very nice result about majorization! Suppose you have states and of a 2-part quantum system. You can trace out one part and get density matrices describing mixed states of the other part, say and . Then Nielsen shows you can get from to using ‘local operations and classical communication’ if and only if majorizes . Note that things are going backwards here compared to how they’ve been going in the rest of this post: if we can get from to , then all forms of entropy go down when we go from to ! This ‘anti-second-law’ behavior is confusing at first, but familiar to me by now. […]

    Reply
  11. Relative Entropy (Part 1) | Azimuth says:
    20 June, 2013 at 5:44 am

    I’m trying to finish off a paper that Tobias Fritz and I have been working on, which gives a category-theoretic (and Bayesian!) characterization of relative entropy. It’s a kind of sequel to our paper with Tom Leinster, in which we characterized entropy.

    Reply
  12. Categories in Control | Azimuth says:
    6 February, 2014 at 7:38 am

    Tobias Fritz, a postdoc at the Perimeter Institute, is working with me on category-theoretic aspects of information theory. We published a paper on entropy with Tom Leinster, and we’ve got a followup on relative entropy that’s almost done. I should be working on it right this instant! But for now, read the series of posts here on Azimuth: Relative Entropy Part 1, Part 2 and Part 3. […]

    Reply
  13. Martin Taylor says:
    7 March, 2015 at 2:03 pm

    Coming from a quite different and quite ancient background, the idea sounds to me to be pretty much Boltzmann’s approach to entropy, but maybe I missed something in the mathematical style, which is unfamiliar to me.

    Boltzmann’s idea (translated into Shannon’s terms) was that the world of possibility could be divided into regions within which changes made no difference to the meaning, but between which changes did matter (microstates within macrostates). For Shannon, information is change in entropy, which means a selection among possible macrostates.

    As Shannon pointed out in the part of the book on continuous systems, although total entropy is not well specified, information is, provided the coordinate system remains constant. The entropy-information partition can be stated as: information from a message (observation) is what you learn about which macrostate the system being observed is in, entropy is what you don’t know about the system as a whole. The latter can be further subdifided into potential information obtainable by further observation (refinement of the macrostate probability distribution) and the possibly infinite remaining unobservable differences in the total system.

    Incidentally, one of the above commenters said that Weaver said entropy had nothing to do with meaning. That’s not what Shannon said. He said that in calculating the capacity of a noisy channel (observation method) one should not consider the meaning, because the meaning of a message (observation) to the receiver (observer) depended entirely on the prior state of the receiver (observer). As does the quantity of information the receiver (observer) could get from the message (observation).

    But maybe I have misinterpreted the message in the original post.

    Reply

You can use Markdown or HTML in your comments. You can also use LaTeX, like this: $latex E = m c^2 $. The word 'latex' comes right after the first dollar sign, with a space after it.

This site uses Akismet to reduce spam. Learn how your comment data is processed.