More Second Laws of Thermodynamics

Oscar Dahlsten is visiting the Centre for Quantum Technologies, so we’re continuing some conversations about entropy that we started last year, back when the Entropy Club was active. But now Jamie Vicary and Brendan Fong are involved in the conversations.

I was surprised when Oscar told me that for a large class of random processes, the usual second law of thermodynamics is just one of infinitely many laws saying that various kinds of disorder increase. I’m annoyed that nobody ever told me about this before! It’s as if they told me about conservation of energy but not conservation of schmenergy, and phlenergy, and zenergy…

So I need to tell you about this. You may not understand it, but at least I can say I tried. I don’t want you blaming me for concealing all these extra second laws of thermodynamics!

Here’s the basic idea. Not all random processes are guaranteed to make entropy increase. But a bunch of them always make probability distributions flatter in a certain precise sense. This makes the entropy of the probability distribution increase. But when you make a probability distribution flatter in this sense, a bunch of other quantities increase too! For example, besides the usual entropy, there are infinitely many other kinds of entropy, called ‘Rényi entropies’, one for each number between 0 and ∞. And a doubly stochastic operator makes all the Rényi entropies increase! This fact is a special case of Theorem 10 here:

• Tim van Erven and Peter Harremoës, Rényi divergence and majorization.

Let me state this fact precisely, and then say a word about how this is related to quantum theory and ‘the collapse of the wavefunction’.

To keep things simple let’s talk about probability distributions on a finite set, though Erven and Harremoës generalize it all to a measure space.

How do we make precise the concept that one probability distribution is flatter than another? You know it when you see it, at least some of the time. For example, suppose I have some system in thermal equilibrium at some temperature, and the probabilities of it being in various states look like this:

Then say I triple the temperature. The probabilities flatten out:

But how can we make this concept precise in a completely general way? We can do it using the concept of ‘majorization’. If one probability distribution is less flat than another, people say it ‘majorizes’ that other one.

Here’s the definition. Say we have two probability distributions $p$ and $q$ on the same set. For each one, list the probabilities in decreasing order:

$p_1 \ge p_2 \ge \cdots \ge p_n$

$q_1 \ge q_2 \ge \cdots \ge q_n$

Then we say $p$ majorizes $q$ if

$p_1 + \cdots + p_k \ge q_1 + \cdots + q_k$

for all $1 \le k \le n.$ So, the idea is that the biggest probabilities in the distribution $p$ add up to more than the corresponding biggest ones in $q.$

In 1960, Alfred Rényi defined a generalization of the usual Shannon entropy that depends on a parameter $\beta.$ If $p$ is a probability distribution on a finite set, its Rényi entropy of order $\beta$ is defined to be

$\displaystyle{ H_\beta(p) = \frac{1}{1 - \beta} \ln \sum_i p_i^\beta }$

where $0 \le \beta < \infty.$ Well, to be honest: if $\beta$ is 0, 1, or $\infty$ we have to define this by taking a limit where we let $\beta$ creep up to that value. But the limit exists, and when $\beta = 1$ we get the usual Shannon entropy

$\displaystyle{ H_1(p) = - \sum_i p_i \ln(p_i) }$

As I explained a while ago, Rényi entropies are important ways of measuring biodiversity. But here’s what I learned just now, from the paper by Erven and Harremoës:

Theorem 1. If a probability distribution $p$ majorizes a probability distribution $q,$ its Rényi entropies are smaller:

$\displaystyle{ H_\beta(p) \le H_\beta(q) }$

for all $0 \le \beta < \infty.$

And here’s what makes this fact so nice. If you do something to a classical system in a way that might involve some randomness, we can describe your action using a stochastic matrix. An $n \times n$ matrix $T$ is called stochastic if whenever $p \in \mathbb{R}^n$ is a probability distribution, so is $T p.$ This is equivalent to saying:

• the matrix entries of $T$ are all $\ge 0,$ and

• each column of $T$ sums to 1.

If $T$ is stochastic, it’s not necessarily true that the entropy of $T p$ is greater than or equal to that of $p,$ not even for the Shannon entropy.

Puzzle 1. Find a counterexample.

However, entropy does increase if we use specially nice stochastic matrices called ‘doubly stochastic’ matrices. People say a matrix $T$ doubly stochastic if it’s stochastic and it maps the probability distribution

$\displaystyle{ p_0 = (\frac{1}{n}, \dots, \frac{1}{n}) }$

to itself. This is the most spread-out probability distribution of all: every other probability distribution majorizes this one.

Why do they call such matrices ‘doubly’ stochastic? Well, if you’ve got a stochastic matrix, each column sums to one. But a stochastic operator is doubly stochastic if and only if each row sums to 1 as well.

Here’s a really cool fact:

Theorem 2. If $T$ is doubly stochastic, $p$ majorizes $T p$ for any probability distribution $p \in \mathbb{R}^n.$ Conversely, if a probability distribution $p$ majorizes a probability distribution $q,$ then $q = T p$ for some doubly stochastic matrix $T$ .

Taken together, Theorems 1 and 2 say that doubly stochastic transformations increase entropy… but not just Shannon entropy! They increase all the different Rényi entropies, as well. So if time evolution is described by a doubly stochastic matrix, we get lots of ‘second laws of thermodynamics’, saying that all these different kinds of entropy increase!

Finally, what does all this have to do with quantum mechanics, and collapsing the wavefunction? There are different things to say, but this is the simplest:

Theorem 3. Given two probability distributions $p, q \in \mathbb{R}^n$ , then $p$ majorizes $q$ if and only there exists a self-adjoint matrix $D$ with eigenvalues $p_i$ and diagonal entries $q_i.$

The matrix $D$ will be a density matrix: a self-adjoint matrix with positive eigenvalues and trace equal to 1. We use such matrices to describe mixed states in quantum mechanics.

Theorem 3 gives a precise sense in which preparing a quantum system in some state, letting time evolve, and then measuring it ‘increases randomness’.

How? Well, suppose we have a quantum system whose Hilbert space is $\mathbb{C}^n.$ If we prepare the system in a mixture of the standard basis states with probabilities $p_i,$ we can describe it with a diagonal density matrix $D_0.$ Then suppose we wait a while and some unitary time evolution occurs. The system is now described by a new density matrix

$D = U D_0 \, U^{-1}$

where $U$ is some unitary operator. If we then do a measurement to see which of the standard basis states our system now lies in, we’ll get the different possible results with probabilities $q_i,$ the diagonal entries of $D.$ But the eigenvalues of $D$ will still be the numbers $p_i.$ So, by the theorem, $p$ majorizes $q$ !

So, not only Shannon entropy but also all the Rényi entropies will increase!

Of course, there are some big physics questions lurking here. Like: what about the real world? In the real world, do lots of different kinds of entropy tend to increase, or just some?

Of course, there’s a huge famous old problem about how reversible time evolution can be compatible with any sort of law saying that entropy must always increase! Still, there are some arguments, going back to Boltzmann’s H-theorem, which show entropy increases under some extra conditions. So then we can ask if other kinds of entropy, like Rényi entropy, increase as well. This will be true whenever we can argue that time evolution is described by doubly stochastic matrices. Theorem 3 gives a partial answer, but there’s probably much more to say.

I don’t have much more to say right now, though. I’ll just point out that while doubly stochastic matrices map the ‘maximally smeared-out’ probability distribution

$\displaystyle{ p_0 = (\frac{1}{n}, \dots, \frac{1}{n}) }$

to itself, a lot of this theory generalizes to stochastic matrices that map exactly one other probability distribution to itself. We need to work with relative Rényi entropy instead of Rényi entropy, and so on, but I don’t think these adjustments are really a big deal. And there are nice theorems that let you know when a stochastic matrix maps exactly one probability distribution to itself, based on the Perron–Frobenius theorem.

References

I already gave you a reference for Theorem 1, namely the paper by Erven and Harremoës, though I don’t think they were the first to prove this particular result: they generalize it quite a lot.

What about Theorem 2? It goes back at least to here:

• Barry C. Arnold, Majorization and the Lorenz Order: A Brief Introduction, Springer Lecture Notes in Statistics 43, Springer, Berlin, 1987.

The partial order on probability distributions given by majorization is also called the ‘Lorenz order’, but mainly when we consider probability distributions on infinite sets. This name presumably comes from the Lorenz curve, a measure of income inequality. This curve shows for the bottom x% of households, what percentage y% of the total income they have:

Puzzle 2. If you’ve got two different probability distributions of incomes, and one majorizes the other, how are their Lorenz curves related?

When we generalize majorization by letting some other probability distribution take the place of

$\displaystyle{ p_0 = (\frac{1}{n}, \dots, \frac{1}{n}) }$

it seems people call it the ‘Markov order’. Here’s a really fascinating paper on that, which I’m just barely beginning to understand:

• A. N. Gorban, P. A. Gorban and G. Judge, Entropy: the Markov ordering approach, Entropy 12 (2010), 1145–1193.

What about Theorem 3? Apparently it goes back to here:

• A. Uhlmann, Wiss. Z. Karl-Marx-Univ. Leipzig 20 (1971), 633.

though I only know this thanks to a more recent paper:

• Michael A. Nielsen, Conditions for a class of entanglement transformations, Phys. Rev. Lett. 83 (1999), 436–439.

By the way, Nielsen’s paper contains another very nice result about majorization! Suppose you have states $\psi$ and $\phi$ of a 2-part quantum system. You can trace out one part and get density matrices describing mixed states of the other part, say $D_\psi$ and $D_\phi$ . Then Nielsen shows you can get from $\psi$ to $\phi$ using ‘local operations and classical communication’ if and only if $D_\phi$ majorizes $D_\psi$ . Note that things are going backwards here compared to how they’ve been going in the rest of this post: if we can get from $\psi$ to $\phi$ , then all forms of entropy go down when we go from $D_\psi$ to $D_\phi$ ! This ‘anti-second-law’ behavior is confusing at first, but familiar to me by now.

When I first learned all this stuff, I naturally thought of the following question—maybe you did too, just now. If $p, q \in \mathbb{R}^n$ are probability distributions and

$\displaystyle{ H_\beta(p) \le H_\beta(q) }$

for all $0 \le \beta < \infty$ , is it true that $p$ majorizes $q$ ?

Apparently the answer must be no, because Klimesh has gone to quite a bit of work to obtain a weaker conclusion: not that $p$ majorizes $q$ , but that $p \otimes r$ majorizes $q \otimes r$ for some probability distribution $r \in \mathbb{R}^m.$ He calls this catalytic majorization, with $r$ serving as a ‘catalyst’:

• Matthew Klimesh, Inequalities that collectively completely characterizes the catalytic majorization relation.

I thank Vlatko Vedral here at the CQT for pointing this out!

Finally, here is a good general introduction to majorization, pointed out by Vasileios Anagnostopoulos:

• T. Ando, Majorization, doubly stochastic matrices, and comparison of eigenvalues, Linear Algebra and its Applications 118 (1989), 163-–248.

This entry was posted on Friday, August 24th, 2012 at 2:13 pm and is filed under information and entropy, physics, probability. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.

48 Responses to More Second Laws of Thermodynamics

amarashiki says:

24 August, 2012 at 3:02 pm

Great post! Two formulae don’t parse, check them (they are at the last paragraph of your article). Cheers from Spain, John…

Reply
- John Baez says:
  
  24 August, 2012 at 4:42 pm
  
  Thanks, I fixed those typos.
  
  Reply
amarashiki says:

24 August, 2012 at 3:21 pm

PS: By the way, I updated some of my older posts on relativity. I included the nonassociative composition rule for adding arbitrary velocities (log of relativistic velocities here http://thespectrumofriemannium.wordpress.com/2012/06/06/log010-relativistic-velocities/ )…Some formulae were indeed studied by Ungar, Sabinin, et alii…I suppose you know that 3 and 7 spatial dimensions are also special in the sense you get a non-associative composition rule for velocities with the aid of the 3d and 7d cross product. So, in 3+1 and 7+1 spacetime dimensions, there are some intrinsic non-associative geometry when you study Lorentz transformations of entities like velocities.I suppose you knew that, but perhaps some reader can be further interested. Nonassociativity rocks! ;)

Reply
some guy on the street says:

25 August, 2012 at 2:29 am

So… the leading partial sums of the order statistics is a universal entropy?

Reply
- John Baez says:
  
  26 August, 2012 at 4:40 am
  
  Yes, there seems to be some truth to that, as formalized by Theorem 2 here. I’m going to try to get this to revolutionize my understanding of thermodynamics. Apparently some quantum chemists already tried, but I don’t have references to their work.
  
  To what extent is the usual Boltzmann–Gibbs–von Neumann–Shannon entropy really important, and to what extent is it just a watered-down version of this ‘universal entropy’? The Gibbs state, i.e. the state of thermal equilibrium with a given expected value of energy, is defined to be the state that maximizes the usual entropy. Is this ‘correct’ or is just ‘good enough for macroscopic systems’? That’s the kind of question I’d like to answer. Of course the problem is figuring out what ‘correct’ means, exactly.
  
  Reply
  - amarashiki says:
    
    10 September, 2012 at 9:16 pm
    
    Is there some entropy for non-equilibrium or dissipative systems? What do you think about the bi-parametric entropies, e.g., Sharma-Mittal entropy or similar quantities?
    
    Reply
Lou Jost says:

26 August, 2012 at 1:15 am

A version of your Theorem 1 is a cornerstone of biodiversity theory, as discussed in a classic article by Patil and Taillie (1982), The diversity concept and its measurement, J. Am. Statistical Ass. 77: 548-561. Incidentally this article proposes the formula for “Tsallis” entropy (which also obeys Theorem 1) some years before Tsallis. (Others predate even these authors.)

Reply
- John Baez says:
  
  26 August, 2012 at 4:48 am
  
  Thanks very much—that’s interesting! As you know, I’ve been trying to figure out what Rényi entropy is really good for in statistical mechanics. Theorems 1 and 2, together with Klimesh’s result on ‘catalytic majorization’ mentioned near the end of my post, combine to give one way to start answering that question. In particular, Klimesh’s result gives a sense in which Rényi entropies (or Hill numbers) are ‘all you need’. The biodiversity people might like that result.
  
  However, I’m also guessing now that Rényi entropies are not all you need to tell if one probability distribution majorizes another. I don’t have a counterexample, but I bet someone does.
  
  Reply
Arrow says:

26 August, 2012 at 8:30 am

So is it possible for Renyi entropies with different beta to change in different directions for some situations? Can one increase while the other decreases or do they all always change in the same direction? (not enough math experience to read the answer from the equation)

Reply
- John Baez says:
  
  26 August, 2012 at 11:02 am
  
  Yes, in general some can increase while others decrease.
  
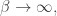  When $\beta$ is big, the Rényi entropy becomes very insensitive to low-probability states: indeed, in the limit $\beta \to \infty,$ it equals the logarithm of the number of most probable states. When $\beta$ is small, Rényi entropy the treats events of different probabilities more even-handedly: in the limit $\beta \to 0,$ it equals the logarithm of the number of states with nonzero probability.
  
  So, if some process increases the number of states with nonzero probability, while decreasing the number of most probable states, some Rényi entropies will go up while others will go down.
  
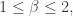  But in fact subtler things can happen, which (say) increase the Rényi entropy for $\beta < 1,$ decrease it for $1 \le \beta \le 2,$ and increase it for $\beta > 2.$ Indeed, arbitrarily complicated patterns can occur.
  
  This is the reason I’m so excited to have learned about a very natural class of random processes that increase all of the Rényi entropies. Instead of obeying just one ‘second law of thermodynamics’, these processes obey many, which aren’t automatic consequences of the usual one!
  
  Reply
  - Alan Cooper says:
    
    18 January, 2013 at 7:17 pm
    
    For the infinite beta case, did you mean to say “logarithm of the *probability* of most probable states”?
    
    Reply
Dmitri Manin says:

28 August, 2012 at 6:35 am

Could it be easier if we change to continuous time by considering matrix $T$ , such that $\exp(T) =$ our doubly stochastic matrix $A$ ? So that vector $p$ evolves under $dp = Tp dt,$ and after one unit of time $p$ becomes $Ap.$ I think $T$ will also be doubly stochastic, although I may be wrong. Then the evolution of $H_\beta$ (how do you enter TeX formulas here?) under $T$ may be easier to understand.

Reply
- John Baez says:
  
  28 August, 2012 at 9:06 am
  
  Dmitri wrote:
  
  how do you enter TeX formulas here?
  
  Thanks to a suggestion from Nadja Kutz, you can find out by reading the box at the top right of this blog.
  
  I think $T$ will also be doubly stochastic, although I may be wrong.
  
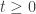  That’s not quite right, but there’s something good to say about this. As I explained Part 5 of the network theory series, the matrices $\exp(t T)$ will be stochastic for all $t \ge 0$ if and only if $T$ is infinitesimal stochastic: its off-diagonal entries are nonnegative and its columns sum to zero.
  
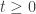  So, I believe the matrices $\exp(t T)$ will be doubly stochastic for all $t \ge 0$ if and only if the the off-diagonal entries of $T$ are nonnegative and its columns and rows sum to zero. I haven’t proved this, but I’ll be utterly shocked if it’s not true. Whatever the correct condition is, I guess we should call such matrices infinitesimal double stochastic.
  
  We could try to calculate the time derivative of the Rényi entropy of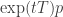 $\exp(t T) p$ for a probability distribution $p$ and show it’s greater than or equal to zero if $p$ is infinitesimal double stochastic.
  
  The theorems I’ve stated already imply that this is true, but this calculation could still be a good way of getting some insight into what’s going on.
  
  Reply
  - nad says:
    
    28 August, 2012 at 1:55 pm
    
    Thanks to a suggestion from Nadja Kutz, you can find out by reading the box at the top right of this blog.
    
    in principle it would be better to have this information directly at the comment box, because currently this information is at a place where not too many people expect this information, moreover it is not highlighted as something which doesn’t belong to a usual sidebar widget. In order to get it close to the comment section you would need to do the following steps on the WordPress Dashboard
    ->Go to Appearances
    ->Click on Editor
    on the right side there are the files of your wordpressinstallation listed under templates
    there should be a comments.php under comments
    –>click on comments
    in the middle section you see then the contents of comments.php somewhere in the test there should be a
    Leave a Reply
    (or something similar)
    which produces the “Leave a Reply” from above
    write one or to under this and then you can write the latex help under this.
    
    Reply
    - nad says:
      
      28 August, 2012 at 1:57 pm
      
      I forgot to comment out the php command, so there should be
      a
      
      /*Leave a Reply
      (or something similar)
    - nad says:
      
      28 August, 2012 at 2:00 pm
      
      ok and now the same again but with hopefully the right syntax for commenting out:
      
      /*Leave a Reply*/
      (or something similar)
    - nad says:
      
      28 August, 2012 at 2:04 pm
      
      ok this didnt help for escaping php. I dont feel like googling now how to escape php in wordpress.
      
      try if you find this:
      
      h3 id=”respond”>Leave a Reply</h3
      
      and then try to write below this.
    - John Baez says:
      
      31 August, 2012 at 4:21 am
      
      Thanks very much—I’ll try your suggestions the next time I have a few minutes for blog improvements!
    - nad says:
      
      3 September, 2012 at 9:14 am
      
      I wrote
      
      in the middle section you see then the contents of comments.php somewhere in the test there should be a
      Leave a Reply
      
      typo: ..somewhere in the text there should be…
      
      I am not sure wether its clear for you what my comments above were about.
      
      the text in the middle (i.e. the content of the file comments.php) is written in (PHP) and I tried to write down the command
      h3 id=”respond”>Leave a Reply</h3
      (in comments.php it should have brackets around) which
      you should look for but this expression
      was executed by wordpress, despite several attempts to escape this.
      
      After you have found this command in comments.php you should be able to write what ever you want after it.
    - nad says:
      
      3 September, 2012 at 9:17 am
      
      After you have found this command in comments.php you should be able to write what ever you want after it.
      
      unless you dont get problems with the latex commands.
John Baez says:

28 August, 2012 at 9:24 am

Over on Google+, Dmitri Manin wrote:

John Baez: this is fascinating, indeed — I encountered Rényi entropies briefly some time ago and wondered what they are good for, now I know. But: is “P majorizes Q” equivalent to “All P’s Rényi entropies are less than those of Q” or is it a one-way implication?

And on your Puzzle 1:

$\left( \begin{array}{cc} 0.1 & 0.1 \\ 0.1 & 0.9 \end{array} \right) \left( \begin{array}{c} 0.5 \\ 0.5 \end{array} \right) = \left( \begin{array}{c} 0.1 \\ 0.0 \end{array} \right)$

Reply
- John Baez says:
  
  28 August, 2012 at 9:32 am
  
  Puzzle solution correct! I’ll copy it over to the blog. In general it would please me immensely if people would post puzzle solutions over on the blog.
  
  You could also replace those 0.1’s and 0.9’s by 0’s and 1’s. Then we’re taking a fair coin, flipping it, and turning it so it surely has heads up.
  
  But: is “P majorizes Q” equivalent to “All P’s Renyi entropies are less than those of Q” or is it a one-way implication?
  
  If you read the ‘references’ section of my post you’ll see my answer, which is (in summary) “they’re probably not equivalent, because someone wrote a long paper to prove an interesting weaker result.”
  
  I would love to see this settled definitively, though. It may have been settled in an earlier paper I haven’t read.
  
  Reply
  - Alan Cooper says:
    
    18 January, 2013 at 7:24 pm
    
    I’m puzzled by your agreement with this solution since the matrix shown is not stochastic. Your description of the effect of replacing 0.1 and 0.9 by 0 and 1 seems to imply that you read it as if the lower left entry and bottom RHS entry were both 0.9 rather than 0.1 and 0.0
    
    Reply
    - Bruce Smith says:
      
      17 January, 2014 at 5:45 pm
      
      I second this puzzlement.
      
      (My own solution to Puzzle 1 was just to let T move every state to the first state (so every column in T looks like 1 0 0 0). Note that this is also one of those T’s for which exactly one probability distribution is fixed, though it’s a degenerate one.)
  - John Baez says:
    
    17 January, 2014 at 10:37 pm
    
    Bruce wrote:
    
    I second this puzzlement.
    
    Sorry for not noticing Alan’s puzzlement earlier.
    
    I probably just typed two characters incorrectly while turning Dmitri’s equation into LaTeX—the matrix given above is not stochastic and the matrix multiplication is done incorrectly! He’s a smart guy, and I liked his solution, so he must have meant this:
    
    $\left( \begin{array}{cc} 0.1 & 0.1 \\ 0.9 & 0.9 \end{array} \right) \left( \begin{array}{c} 0.5 \\ 0.5 \end{array} \right) = \left( \begin{array}{c} 0.1 \\ 0.9 \end{array} \right)$
    
    Bruce wrote:
    
    My own solution to Puzzle 1 was just to let T move every state to the first state.
    
    Yes, mine too—that’s why I had replied to Dmitri as follows:
    
    You could also replace those 0.1′s and 0.9′s by 0′s and 1′s. Then we’re taking a fair coin, flipping it, and turning it so it surely has heads up.
    
    Reply
John Baez says:

28 August, 2012 at 9:58 am

Here’s another cute fact:

Theorem. Suppose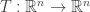 $T : \mathbb{R}^n \to \mathbb{R}^n$ is a stochastic matrix. Then the following are equivalent:

1) For some $0 < \alpha < \infty$ , all probability distributions $p \in \mathbb{R}^n$ obey:

$H_\alpha(T p) \ge H_\alpha(p)$

2) For all $0 < \alpha < \infty$ , all probability distributions $p \in \mathbb{R}^n$ obey:

$H_\alpha(T p) \ge H_\alpha(p)$

3) $T$ is doubly stochastic.

Proof. That 3) implies 2) is Theorem 1 in the blog post. That 2) implies 1) is obvious. So, we just need to prove 1) implies 3). The key is that

$\displaystyle{ p = \left(\frac{1}{n}, \dots, \frac{1}{n}\right) }$

is the unique probability distribution maximizing the Rényi entropy for $0 < \alpha < \infty.$ So, if

$H_\alpha(T p) \ge H_\alpha(p)$

we see that

$T p = p$

but in the blog post we’ve seen this is equivalent to $T$ being doubly stochastic. █

Reply
- John Baez says:
  
  28 August, 2012 at 10:06 am
  
  So, there’s a sense in which there’s not lots of 2nd laws of thermodynamics: a stochastic matrix that increases one Rényi entropy for all probability distributions increases all of them.
  
  But there’s still a sense in which there are lots of 2nd laws: a probability distribution can have one of its Rényi entropies greater than the corresponding Rényi entropy of some other probability distribution, without having all of its Rényi entropies be greater.
  
  Reply
Dmitri Manin says:

28 August, 2012 at 7:49 pm

That’s a good summary. I wonder if there are interesting classes of evolution operators that drive different Renyi entropies in different directions.

Reply
An Entropy Challenge « Azimuth says:

29 August, 2012 at 3:54 pm

Can one probability distribution have all its Rényi entropies less than another, yet fail to majorize it? This question came up near the end of my post More Second Laws of Thermodynamics. Now let’s settle it […]

Reply
arch1 says:

31 August, 2012 at 9:51 pm

Here’s my abortive attempt at Puzzle #2-

1) The Lorenz curve is the integral of the inverse of the integral of the probability distribution of income (OK, normalized to make it a percentage).
2) So one restatement is: When you majorize a probability distribution (roughly, when you make it “less flat”), what happens to the normalized integral of the inverse of its integral?
3) I have no clue.
4) OK let’s try a few:
a. The Lorenz curve La of the uniform distribution (N equally populated income brackets, assume equally spaced) approximates a parabola.
b. The Lorenz curve Lb of a “spike” distribution (all incomes identical) is a diagonal line which lies above La.
c. The Lorenz curve Lc of a “half-impoverished-half-rich” distribution crosses La.
d. There are also distributions whose Lorenz curves lie on-or-below La.

Hmm. Distributions b-d all majorize a; but their Lorenz curves are all over the map (at least, in the respects I’m considering) relative to a’s.

..So I got nothing. Would one of you do the humane thing and post a solution? Quickly please, this is getting ugly.

Reply
- John Baez says:
  
  1 September, 2012 at 3:22 am
  
  arch 1 wrote:
  
  The Lorenz curve is the integral of the inverse of the integral of the probability distribution of income (OK, normalized to make it a percentage).
  
  No, that’s not true: it’s simpler than that. This is why you got stuck. The Lorenz curve shows for the bottom x% of households, what percentage y% of the total income they have. So, for example, if everyone has the same income the Lorenz curve is a diagonal straight line, as shown here:
  
  The case where everyone has the same income is a bit degenerate, but in this case “the bottom x% of households” just means “any x% of households”. Everyone is at the bottom and everyone is at the top, in this case!
  
  Reply
  - arch1 says:
    
    24 September, 2012 at 4:51 pm
    
    Thanks John for this reply which I just saw.
    
    I think I did understand the definition of the Lorenz curve (as a check on this I got the same answer to the example you cite; it is my case 4b).
    
    But I don’t yet understand why my statement which you quoted is not true. I need to think about that, since as you imply it may help get me unstuck.
    
    Reply
Network Theory for Economists « Azimuth says:

15 January, 2013 at 11:32 pm

Evolutionary games and the 2nd law of thermodynamics […]

Reply
Arnob Alam says:

3 December, 2013 at 10:13 am

John Baez:

Thank you for the wonderful post. I believe the idea of majorization comes from the work of Hardy, Littlewood and Polya:

http://books.google.com/books?isbn=0521358809

Is the parameter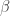 $\beta$ the same as the inverse temperature $\beta = \frac {1}{T}$ found in the Boltzmann distribution, or is this a different 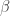$\beta$ altogether?

(warning: not a physicist, just an undergraduate economist :-)

Reply
nad says:

16 January, 2014 at 8:32 am

John wrote:

But the limit exists, and when $\beta = 1$ we get the usual Shannon entropy

I have troubles to recover this. Do you assume an infinite particle number? Because if no then if I perform L’Hôpital’s rule I get -1 for the denominator and for the nominator
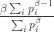$\frac{\beta \sum_i p_i^{\beta-1}}{\sum_i p_i^{\beta}}$ , i.e.
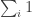the particle number $\sum_i 1$ . Sorry can’t find the error.

Is there a way to recover the relative Shannon entropy from a generalized version of a Renyi entropy?

Reply
- nad says:
  
  16 January, 2014 at 8:59 am
  
  Is there a way to recover the relative Shannon entropy from a generalized version of a Renyi entropy? or the free energy mentioned by you here ?
  
  Reply
- Graham Jones says:
  
  16 January, 2014 at 10:04 am
  
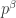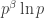  The derivative of $p^\beta$ with respect to $\beta$ (not p!) is $p^\beta \ln p$ .
  
  Reply
- John Baez says:
  
  16 January, 2014 at 3:14 pm
  
  If you use L’Hôpital’s rule correctly you should get
  
  $\displaystyle{ \lim_{\beta \to 1} \frac{1}{1 - \beta} \ln \sum_i p_i^\beta } = - \sum_i p_i \ln pi_i$
  
  My hunch is that you’re not remembering the right formula for
  
  $\displaystyle{ \frac{d}{d \beta} p^\beta }$
  
  It’s a famous mistake to get confused and guess
  
  $\beta p^{\beta - 1}$
  
  Graham gave you the correct formula:
  
  $\displaystyle{ p^\beta \ln p }$
  
  See, it’s a classic trick to ask calculus students to compute things like
  
  $\displaystyle{ \frac{d}{d n} x^n }$
  
  or
  
  $\displaystyle{ \frac{d}{d n} n^x }$
  
  and watch them get confused.
  
  Reply
  - nad says:
    
    16 January, 2014 at 5:30 pm
    
    graham wrote
    
    The derivative of $p^\beta$ with respect to $\beta$ (not p!) is $p^\beta \ln p.$
    
    oh ! thats true. thanks.
    
    John wrote
    
    See, it’s a classic trick to ask calculus students to compute …and watch them get confused.
    
    I knew that trick! That knowledge didn’t help though. I guess I have a bad hairror day.
    
    Reply
- John Baez says:
  
  16 January, 2014 at 7:12 pm
  
  Nad wrote:
  
  Is there a way to recover the relative Shannon entropy from a generalized version of a Rényi entropy?
  
  Yes, relative Shannon entropy is the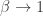 $\beta \to 1$ limit of relative Rényi entropy:
  
  $\displaystyle{ \lim_{\beta \to 1} \frac{1}{1 - \beta} \ln \sum_i p_i^\beta q_i^{1 - \beta} = - \sum_i p_i \ln \left( \frac{p_i}{q_i} \right) }$
  
  where
  
  $\displaystyle{ - \sum_i p_i \ln \left( \frac{p_i}{q_i} \right) }$
  
  is the Shannon entropy of $p$ relative to $q$ and
  
  $\displaystyle{ \frac{1}{1 - \beta} \ln \sum_i p_i^\beta q_i^{1 - \beta} }$
  
  is the Rényi entropy of $p$ relative to $q.$ The negative of relative Rényi entropy is called the Rényi divergence, and you can read more about it here:
  
  • Tim van Erven and Peter Harremoës, Rényi divergence and majorization.
  
  I worked out the relation between Rényi entropy and free energy here:
  
  • Rényi entropy and free energy, Azimuth, 10 February 2011.
  
  In a nutshell, Rényi entropy is proportional to the change in free energy as we suddenly reduce the temperature of a system.
  
  Reply
  - nad says:
    
    17 January, 2014 at 8:53 am
    
    Thanks for the comments.
    
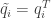    I find that $T=1$ constraint in here is a a bit irritating. But indeed it seems if one supplies the relative Rényi entropy with an overall factor $T$ and defines $\tilde{q_i}= q_i^T$ and $\tilde{\beta} =\frac{1}{T} \beta$ one should get for the relative Rényi entropy in those tilde variables:
    
    $\frac{T}{T(\frac{1}{T}-\tilde{\beta})} \sum_i p_i^{T\tilde{\beta}} \tilde{q}_i^{(\frac{1}{T}-\tilde{\beta})}$
    
    and this should go for $\tilde{\beta} \rightarrow \frac{1}{T}$ to the free energy term you gave in here (….if there aren’t again embarrassing errors)
    but the problem here is of course: the $\tilde{q}_i$ don’t sum to 1 that is it seems if one would like to get this more general term of free energy then this may eventually require some strange
    $\frac{1}{(\frac{1}{T}-{\beta})} \sum_i p_i^{T{\beta}} \tilde{q}_i^{(\frac{1}{T}-{\beta})}$ “modifed” version of the relative Rényi entropy, which goes to the “usual” Renyi entropy for $T \rightarrow 1$
    
    Reply
    - John Baez says:
      
      17 January, 2014 at 11:37 pm
      
      Nad wrote:
      
      I find that $T=1$ constraint in here is a a bit irritating.
      
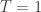      That $T = 1$ constraint was in the initial blog article, but we removed it in the following discussion. If you want to avoid reading the discussion, go straight to the arXiv paper I cited in the blog article:
      
      • John Baez, Rényi entropy and free energy, 6 June 2011.
      
      This is more polished than the initial blog article. Here’s the abstract:
      
      The Rényi entropy is a generalization of the usual concept of entropy which depends on a parameter q. In fact, Rényi entropy is closely related to free energy. Suppose we start with a system in thermal equilibrium and then suddenly divide the temperature by q. Then the maximum amount of work the system can do as it moves to equilibrium at the new temperature, divided by the change in temperature, equals the system’s Rényi entropy in its original state. This result applies to both classical and quantum systems. Mathematically, we can express this result as follows: the Rényi entropy of a system in thermal equilibrium is minus the “1/q-derivative” of its free energy with respect to temperature. This shows that Renyi entropy is a q-deformation of the usual concept of entropy.
    - nad says:
      
      18 January, 2014 at 8:20 am
      
      After the comment showed up I detected some typos. I wrote
      
      $\frac{1}{(\frac{1}{T}-{\beta})} \sum_i p_i^{T{\beta}} \tilde{q}_i^{(\frac{1}{T}-{\beta})}$ “modifed” version of the relative Rényi entropy, which goes to the “usual” Renyi entropy for $T \rightarrow 1$
      
      this should read:
      
      $\frac{1}{(\frac{1}{T}-{\beta})} \sum_i p_i^{T{\beta}} {q}_i^{(\frac{1}{T}-{\beta})}$ “modifed” version of the relative Rényi entropy, which goes to the “usual” relative Renyi entropy for $T \rightarrow 1$
      
      That is in particular one gets the “nonrelative” Rényi entropy with a “fudge factor” if one uses the distribution $q_i = \frac{1}{N}$ , $N$ being the particle number. The fudge factor is then
      $\frac{1}{N}^{(\frac{1}{T}-\beta)}.$
      
      Thanks for the comment. Unfortunately I haven’t followed the free energy discussion as closely as I should in order to comment here. I even didn’t notice that you had written an article in this area. I just now briefly looked at the article. “Briefly” because looking at this is for me now a “hobby” to which I rather should not devote too much time given my current “pension plan”….this should serve as an excuse if my comments here should not fully follow the line, like if I didn’t read some comments etc.
      
      Anyways, it is a nice result that the Rényi entropy is the q-deformed derivative of the free energy with respect to $T$ .
      
      And your $T$ seems to be what is my $\frac{1}{T}$ and your $T_0 =\beta$ , that is if I use the above special distribution $q_i = \frac{1}{N}$ then one would get your Rényi entropy (in your variables) by multiplying with the “fudge factor” $\frac{T}{(\frac{1}{N})^{(T-T_0}}.$
      
      So if the above modified expression should make sense at all than the relative Rényi entropy seems to be some kind of strange “q-integral” of the Rényi entropy at the “critical temperature” that is if $T \rightarrow T_0.$
    - nad says:
      
      27 February, 2014 at 7:37 am
      
      I just noticed that the factor T in here goes of course over both summands :O. So the “modified” relative Renyi entropy should read
      
      $\displaystyle{ \frac{1}{(\frac{1}{T}-{\beta})} \ln \sum_i p_i^{T{\beta}} {q}_i^{(1-{T \beta})} }$
      
      and the corresponding “fudge factor” giving your modified “nonrelative” Renyi entropy (with the above change of parameters) would then be
      
      $\displaystyle{ \frac{T}{\frac{1}{N}^{(1-\frac{T_0}{T})}} }$
      
      On the other hand one could treat the two summands differently in order to deal with the “rescalability” of the energy:
      
      Speaking of ambiguities, our choice of inverse temperature $\beta$ was arbitrary as long as it’s not zero. If we multiply $\beta$ by some number and divide all the energies by that same number, the numbers $\exp(-\beta E_i)$ and thus the probabilities $p_i$ don’t change.
      
      That is with a “modified” relative Renyi entropy which reads as
      
      $\displaystyle{ \frac{1}{\frac{1}{T_1}-\beta} \ln \sum_i p_i^{T_1{\beta}} {q}_i^{(\frac{T_2}{T_1}-{T_2 \beta})} }$
      
      one should get in the limit $\beta \rightarrow 1/T_1$ a “modified” relative Shannon entropy:
      
      $\displaystyle{ -\sum_i T_1 p_i \ln p_i - T_2 p_i \ln q_i }$
    - nad says:
      
      27 February, 2014 at 10:05 am
      
      Why could this be interesting? For example here you wrote
      
      $RE((g,t)∘(f,s))=RE(g,t)+RE(f,s).$ on a first reading (warning: I don’t fully understand that category thing and I don’t want to spend to much time on studying it) this looks vaguely like a triangle equation. I. e. relative Renyi entropy looks like a “deformed” (unsymmetric) metric. And in fact if p and q are not too far apart then it seems you explained this already – if my interpretation of reading this Fisher information blog post diagonally is right.
      I don’t know wether this also holds for this “modified” version but by fastly setting e.g.
      $T_2 := \frac{T_1^2}{1-T_1\beta}$ and $\beta = \frac{1}{2T_1}$ it seems one would get
      $\frac{1}{2 T_1} \ln \sum_i p_i^{\frac{1}{2}} q_i^{\frac{1}{2}}$ which looks -eventually apart from a minus sign- on a first glance like it could be a metric, but I might be totally wrong. At least if it is than it should be known.
    - nad says:
      
      27 February, 2014 at 11:09 am
      
      First Typo detected: $\frac{1}{2T_1} -> 2 T_1$ in the last formula
    - nad says:
      
      23 March, 2014 at 6:50 am
      
      Yet another typo. In some of the comments above I forgot the log. As a consequence I forgot to take the log in the case $q_i = \frac{1}{N}$ . That is for comparing your fudge factor and mine one would need to take also a constant offset into account.
Is the Renyi entropy an invertible functional of ordered probability distributions? – Math Solution says:

10 March, 2022 at 4:15 pm

[…] this has been called the “spectrum of Renyi information”. The Renyi entropies are notable for being non-increasing under doubly stochastic operations ($vec{p} to Tvec{p}$ for doubly stochastic matrix $T$) and […]

Reply

You can use Markdown or HTML in your comments. You can also use LaTeX, like this: $latex E = m c^2 $. The word 'latex' comes right after the first dollar sign, with a space after it. Cancel reply

This site uses Akismet to reduce spam. Learn how your comment data is processed.

	John Baez on Agent-Based Models (Part …
	Grandpa D on Agent-Based Models (Part …
	Anton Sherwood on Well Temperaments (Part 3…
	John Baez on Well Temperaments (Part 3…
	Anton Sherwood on Well Temperaments (Part 3…
	John Baez on Hexagonal Tiling Honeycomb
	Victor V Albert on Hexagonal Tiling Honeycomb
	Matias Schrauf on Agent-Based Models (Part …
	John Tromp on The Busy Beaver Game
	Wolfgang on Protonium

Azimuth