guest post by Manoj Gopalkrishnan
A few weeks back, I promised to tell you more about a long-standing open problem in reaction networks, the ‘global attractor conjecture’. I am not going to quite get there today, but we shall take one step in that direction.
Today’s plan is to help you make friends with a very useful function we will call the ‘free energy’ which comes up all the time in the study of chemical reaction networks. We will see that for complex-balanced systems, the free energy function decreases along trajectories of the rate equation. I’m going to explain this statement, and give you most of the proof!
The point of doing all this work is that we will then be able to invoke Lyapunov’s theorem which implies stability of the dynamics. In Greek mythology, Sisyphus was cursed to roll a boulder up a hill only to have it roll down again, so that he had to keep repeating the task for all eternity. When I think of an unstable equilibrium, I imagine a boulder delicately balanced on top of a hill, which will fall off if given the slightest push:

or, more abstractly:

On the other hand, I picture a stable equilibrium as a pebble at the very bottom of a hill. Whichever way a perturbation takes it is up, so it will roll down again to the bottom:

Lyapunov’s theorem guarantees stability provided we can exhibit a nice enough function that decreases along trajectories. ‘Nice enough’ means that, viewing
as a height function for the hill, the equilibrium configuration should be at the bottom, and every direction from there should be up. If Sisyphus had dug a pit at the top of the hill for the boulder to rest in, Lyapunov’s theorem would have applied, and he could have gone home to rest. The moral of the story is that it pays to learn dynamical systems theory!
Because of the connection to Lyapunov’s theorem, such functions that decrease along trajectories are also called Lyapunov functions. A similar situation is seen in Boltzmann’s H-theorem, and hence such functions are sometimes called H-functions by physicists.
Another reason for me to talk about these ideas now is that I have posted a new article on the arXiv:
• Manoj Gopalkrishnan, On the Lyapunov function for complex-balanced mass-action systems.
The free energy function in chemical reaction networks goes back at least to 1972, to this paper:
• Friedrich Horn and Roy Jackson, General mass action kinetics, Arch. Rational Mech. Analysis 49 (1972), 81–116.
Many of us credit Horn and Jackson’s paper with starting the mathematical study of reaction networks. My paper is an exposition of the main result of Horn and Jackson, with a shorter and simpler proof. The gain comes because Horn and Jackson proved all their results from scratch, whereas I’m using some easy results from graph theory, and the log-sum inequality.
We shall be talking about reaction networks. Remember the idea from the network theory series. We have a set whose elements are called species, for example
A complex is a vector of natural numbers saying how many items of each species we have. For example, we could have a complex But chemists would usually write this as
A reaction network is a set of species and a set
of transitions or reactions, where each transition
goes from some complex
to some complex
For example, we could have a transition
with
and
In this situation chemists usually write
but we want names like for our transitions, so we might write
or
As John explained in Part 3 of the network theory series, chemists like to work with a vector of nonnegative real numbers saying the concentration of each species at time
If we know a rate constant
for each transition
we can write down an equation saying how these concentrations change with time:
This is called the rate equation. It’s really a system of ODEs describing how the concentration of each species change with time. Here an expression like is shorthand for the monomial
John and Brendan talked about complex balance in Part 9. I’m going to recall this definition, from a slightly different point of view that will be helpful for the result we are trying to prove.
We can draw a reaction network as a graph! The vertices of this graph are all the complexes where
The edges are all the transitions
We think of each edge
as directed, going from
to
We will call the map that sends each transition to the positive real number
the flow
on this graph. The rate equation can be rewritten very simply in terms of this flow as:
where the right-hand side is now a linear expression in the flow
Flows of water, or electric current, obey a version of Kirchhoff’s current law. Such flows are called conservative flows. The following two lemmas from graph theory are immediate for conservative flows:
Lemma 1. If f is a conservative flow then the net flow across every cut is zero.
A cut is a way of chopping the graph in two, like this:
It’s easy to prove Lemma 1 by induction, moving one vertex across the cut at a time.
Lemma 2. If a conservative flow exists then every edge is part of a directed cycle.
Why is Lemma 2 true? Suppose there exists an edge that is not part of any directed cycle. We will exhibit a cut with non-zero net flow. By Lemma 1, this will imply that the flow is not conservative.
One side of the cut will consist of all vertices from which is reachable by a directed path in the reaction network. The other side of the cut contains at least
since
is not reachable from
by the assumption that
is not part of a directed cycle. There is flow going from left to right of the cut, across the transition
Since there can be no flow coming back, this cut has nonzero net flow, and we’re done. ▮
Now, back to the rate equation! We can ask if the flow is conservative. That is, we can ask if, for every complex
:
In words, we are asking if the sum of the flow through all transitions coming in to equals the sum of the flow through all transitions going out of
If this condition is satisfied at a vector of concentrations
so that the flow
is conservative, then we call
a point of complex balance. If in addition, every component of
is strictly positive, then we say that the system is complex balanced.
Clearly if is a point of complex balance, it’s an equilibrium solution of the rate equation. In other words,
is a solution of the rate equation, where
never changes.
I’m using ‘equilibrium’ the way mathematicians do. But I should warn you that chemists use ‘equilibrium’ to mean something more than merely a solution that doesn’t change with time. They often also mean it’s a point of complex balance, or even more. People actually get into arguments about this at conferences.
Complex balance implies more than mere equilibrium. For starters, if a reaction network is such that every edge belongs to a directed cycle, then one says that the reaction network is weakly reversible. So Lemmas 1 and 2 establish that complex-balanced systems must be weakly reversible!
From here on, we fix a complex-balanced system, with a strictly positive point of complex balance.
Definition. The free energy function is the function
where the sum is over all species in
The whole point of defining the function this way is because it is the unique function, up to an additive constant, whose partial derivative with respect to is
This is important enough that we write it as a lemma. To state it in a pithy way, it is helpful to introduce vector notation for division and logarithms. If
and
are two vectors, we will understand
to mean the vector
such that
coordinate-wise. Similarly
is defined in a coordinate-wise sense as the vector with coordinates
Lemma 3. The gradient of
equals
We’re ready to state our main theorem!
Theorem. Fix a trajectory of the rate equation. Then
is a decreasing function of time
Further, it is strictly decreasing unless
is an equilibrium solution of the rate equation.
I find precise mathematical statements reassuring. You can often make up your mind about the truth value from a few examples. Very often, though not always, a few well-chosen examples are all you need to get the general idea for the proof. Such is the case for the above theorem. There are three key examples: the two-cycle, the three-cycle, and the figure-eight.
The two-cycle. The two-cycle is this reaction network:

It has two complexes and
and two transitions
and
with rates
and
respectively.
Fix a solution of the rate equation. Then the flow from
to
equals
and the backward flow equals
The condition for
to be a conservative flow requires that
This is one binomial equation in at least one variable, and clearly has a solution in the positive reals. We have just shown that every two-cycle is complex balanced.
The derivative can now be computed by the chain rule, using Lemma 3. It works out to
times
This is never positive, and it’s zero if and only if
Why is this? Simply because the logarithm of something greater than 1 is positive, while the log of something less than 1 is negative, so that the sign of is always opposite the sign of
We have verified our theorem for this example.
(Note that occurs when
but also at other points: in this example, there is a whole hypersurface consisting of points of complex balance.)
In fact, this simple calculation achieves much more.
Definition. A reaction network is reversible if for every transition there is a transition
going back, called the reverse of
Suppose we have a reversible reaction network and a vector of concentrations
such that the flow along each edge equals that along the edge going back:
whenever is the reverse
Then we say the reaction network is detailed balanced, and
is a point of detailed balance.
For a detailed-balanced system, the time derivative of is a sum over the contributions of pairs consisting of an edge and its reverse. Hence, the two-cycle calculation shows that the theorem holds for all detailed balanced systems!
This linearity trick is going to prove very valuable. It will allow us to treat the general case of complex balanced systems one cycle at a time. The proof for a single cycle is essentially contained in the example of a three-cycle, which we treat next:
The three-cycle. The three-cycle is this reaction network:

We assume that the system is complex balanced, so that
Let us call this nonnegative number A small calculation employing the chain rule shows that
equals
times
We need to think about the sign of this quantity:
Lemma 3. Let be positive numbers. Then
is less than or equal to zero, with equality precisely when
The proof is a direct application of the log sum inequality. In fact, this holds not just for three numbers, but for any finite list of numbers. Indeed, that is precisely how one obtains the proof for cycles of arbitrary length. Even the two-cycle proof is a special case! If you are wondering how the log sum inequality is proved, it is an application of Jensen’s inequality, that workhorse of convex analysis.
The three-cycle calculation extends to a proof for the theorem so long as there is no directed edge that is shared between two directed cycles. When there are such edges, we need to argue that the flows and
can be split between the cycles sharing that edge in a consistent manner, so that the cycles can be analyzed independently. We will need the following simple lemma about conservative flows from graph theory. We will apply this lemma to the flow
Lemma 4. Let be a conservative flow on a graph
Then there exist directed cycles
in
and nonnegative real ‘flows’
such that for each directed edge
in
the flow
equals the sum of
over
such the cycle
contains the edge
Intuitively, this lemma says that conservative flows come from constant flows on the directed cycles of the graph. How does one show this lemma? I’m sure there are several proofs, and I hope some of you can share some of the really neat ones with me. The one I employed was algorithmic. The idea is to pick a cycle, any cycle, and subtract the maximum constant flow that this cycle allows, and repeat. This is most easily understood by looking at the example of the figure-eight:
The figure-eight. This reaction network consists of two three-cycles sharing an edge:

Here’s the proof for Lemma 4. Let be a conservative flow on this graph. We want to exhibit cycles and flows on this graph according to Lemma 4. We arbitrarily pick any cycle in the graph. For example, in the figure-eight, suppose we pick the cycle
We pick an edge in this cycle on which the flow is minimum. In this case,
is the minimum. We define a remainder flow by subtracting from
this constant flow which was restricted to one cycle. So the remainder flow is the same as
on edges that don’t belong to the picked cycle. For edges that belong to the cycle, the remainder flow is
minus the minimum of
on this cycle. We observe that this remainder flow satisfies the conditions of Lemma 4 on a graph with strictly fewer edges. Continuing in this way, since the lemma is trivially true for the empty graph, we are done by infinite descent.
Now that we know how to split the flow across cycles, we can figure out how to split the rates across the different cycles. This will tell us how to split the flow
across cycles. Again, this is best illustrated by an example.
The figure-eight. Again, this reaction network looks like

Suppose as in Lemma 4, we obtain the cycles
with constant flow
and
with constant flow
such that
Here’s the picture:

Then we obtain rates and
by solving the equations
Using these rates, we can define non-constant flows on
and
on
by the usual formulas:
and similarly for In particular, this gives us
and similarly for
Using this, we obtain the proof of the Theorem! The time derivative of along a trajectory has a contribution from each cycle
as in Lemma 4, where each cycle is treated as a separate system with the new rates
and the new flows
and
So, we’ve reduced the problem to the case of a cycle, which we’ve already done.
Let’s review what happened. The time derivative of the function has a very nice form, which is linear in the flow
The reaction network can be broken up into cycles. Th e conservative flow
for a complex balanced system can be split into conservative flows on cycles by Lemma 4. This informs us how to split the non-conservative flow
across cycles. By linearity of the time derivative, we can separately treat the case for every cycle. For each cycle, we get an expression to which the log sum inequality applies, giving us the final result that
decreases along trajectories of the rate equation.
Now that we have a Lyapunov function, we will put it to use to obtain some nice theorems about the dynamics, and finally state the global attractor conjecture. All that and more, in the next blog post!


Great article! I’ve got a number of questions. The first is, how does your proof simplify the arguments used, say, here:
• Jonathan M. Guberman, Mass Action Reaction Networks and the Deficiency Zero Theorem, B.A. thesis, Department of Mathematics, Harvard University, 2003.
This thesis is mainly a review of known stuff, so I imagine his proof that free energy is a Lyapunov function is similar to Horn and Jackson’s; I’m just citing this because it’s a nice self-contained treatment of the deficiency zero theorem, and some things seem to have been cleaned up.
He defines the free energy function on page 28 of the PDF file (which is numbered page 26—don’t you just hate that?). Starting on page 30 he proves stuff about it for “cyclic systems”, and starting on page 34 he talks about a “generalization to non-cyclic systems”, saying at one point
This sounds like your argument using “infinite descent”.
Your argument looks simpler and shorter to me, but not having read this part of Glauberman’s thesis in detail I’m curious what your main simplifications actually were!
Hi John,
Thanks! And thanks for your help in editing this document!
Thanks for pointing me to Guberman’s B. A. thesis, I hadn’t looked at it before. The observation that the analysis for a complex balanced system can be broken down into analysis on cycles was one of the key ideas in Horn and Jackson’s paper! Perhaps I should have stressed this more.
My simplifications are:
1. Lemma 7.2 in Guberman’s thesis. Horn and Jackson prove a similar lemma in their Appendix. I prove this by invoking the log-sum inequality, a trick which was actually first pointed out to me by my colleague Pranab Sen.
2. Writing the decomposition lemmas in the language of cuts and flows makes some steps more transparent. For example, I am able to state Lemma 4 for graphs, and then apply it to reaction networks.
Thanks for this fine article.
You wrote: “For a detail-balanced system, the time derivative of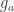 is a sum over the contributions of pairs consisting of an edge and its reverse.” Can you write out this statement more formally. Thanks.
is a sum over the contributions of pairs consisting of an edge and its reverse.” Can you write out this statement more formally. Thanks.
Hi David,
Thanks, and also thank you for the useful comments at the draft stage.
By the chain rule, the time derivative of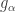 equals:
equals:
We wrote the rate equation in terms of the flow as:
So we can write
Now it is up to us how we want to collect terms in this sum. If the system is detailed balanced, we collect a transition and its reverse together. If the system is complex-balanced, we decompose into cycles, also decomposing the flows appropriately, and collect terms for each cycle. Hope that helped!
Here’s another question. You mention how chemists tend to mean a lot more by ‘equilibrium’ than merely time-independence. It seems not just complex balance but detailed balance is often considered a fundamental law for chemical systems in equilibrium. For example, Wikipedia says:
So, I wonder what conditions on a reaction network imply that every point of complex balance is a point of detailed balance? The simplest most obvious guess is that the reaction network be reversible! This is obviously necessary, but is it sufficient?
Yes, John, in many communities “equilibrium” automatically means “detailed-balanced.”
No it is not sufficient. I think it was Bernd Sturmfels who pointed out to me that there are reversible reaction networks that are complex balanced but not detailed balanced! And these are not hard to find, you should be able to find a 3-cycle on two species that satisfies this property.
Okay, thanks. This raises an interesting question, then. Since in chemistry detailed balance seems to be a “law of nature” for systems in equilibrium, there should be some property of “realistic” reaction networks that guarantees the existence of points of detailed balance. What is this property?
Maybe this property should guarantee the existence of at least one point of detailed balance per conservation class. Maybe it should guarantee that every point of complex balance is a point of detailed balance. Or maybe it should be weaker.
Looking at the counterexample you mention, and seeing what if anything is “unrealistic” about it, may help us understand this issue—if nobody has figured it out already.
Getting some conditions that pick out “realistic” reaction networks could be interesting, for many reasons. For example, maybe it’s easier to prove the Global Attractor Conjecture for “realistic” networks.
Hi John,
Next time I will show that:
• If a reaction network is complex-balanced, then every non-negative equilibrium is complex-balanced. Further, within every conservation class, there is precisely one positive equilibrium — which of course is complex-balanced by what I said above.
• If a reaction network is detailed-balanced, then every non-negative equilibrium is detailed-balanced. Further, within every conservation class, there is precisely one positive equilibrium.
Detailed-balance is a manifestation of “microscopic reversibility.” By Noether’s theorem, this leads to a conserved quantity, i.e., energy. Indeed, if we assign an energy to each species, then detailed-balance is the condition that there are no energy cycles. We present this idea in our paper:
On the Mathematics of the Law of Mass Action. In other words, detailed balance == first law of thermodynamics.
Indeed it is easier to prove the Global Attractor Conjecture for “realistic” networks! We do this also in our paper linked above! We introduce the notion of “Atomic” reaction networks, where there are some elementary species called atoms, and all other species are made out of atoms in a unique way. Further, reactions preserve atoms. For such networks that satisfy detailed balance, we are able to show the global attractor conjecture.
The autocatalysis result I spoke about in my last post is in fact a generalization of this initial result. The sequence of results goes thus: all atomic systems are “prime” – they generate prime ideals in some appropriate sense. All prime systems are non-catalytic. All non-catalytic systems are non-autocatalytic. We can prove that non-autocatalytic systems are precisely the ones without critical siphons, thus obtaining the Global Attractor Conjecture for all non-autocatalytic complex-balanced systems. These ideas are developed in the three papers:
On the Mathematics of the Law of Mass Action
Catalysis in Reaction Networks Bull. Math Biol. 2011, 73:2962-2982,
Autocatalysis in Reaction Networks
Great! I’ll need to read these 3 papers. They sound very interesting.
The results in your paper On the mathematics of the law of mass action seem very important. I need to read this paper and thoroughly understand it. But the term ‘event-system’ is a bit off-putting to me. I need to make sure I can translate results about event-systems into results about chemical reaction networks. Maybe you can help me.
Is a ‘finite, physical event-system’ the same as what I’d call a ‘reaction network’ with some finite set of species, finite set of transitions (=reactions), and a positive rate constant for each transition?
I’m really glad your paper On the mathematics of the law of mass action introduces the concept of a reaction network where each species has an energy. This indeed sounds like just the right idea if you want detailed balance!
Has someone studied how this concept of energy is related to the concept of ‘free energy’ discussed in this post? There should be a theorem for this class of reaction networks saying
If nobody has proved it yet, we should do it now!
I’ll say a bit about this below, in the special case of reversible reaction networks where each transition has just a single species as input and a single species as output.
Great article!
I have a problem; the mathematical description of the chemical reaction is true for great number of molecules, so that if it used a little number of molecules, or if the concentration of the gas is low, then the reaction network have not fixed the rate constants (it seem, to me, that there are rate constant fluctuations); it seem, to me, that it is not like a cross section that have a fixed value, because of – here – there is a probability of the trajectories crossing.
If the rate constants are not fixed, then there is a fluctuation of the chemical reactions.
But if this is true for low concentrations, then this is true ever (there is not a clear separation between low density and high density, with ever a little reaction fluctuations).
With low numbers of molecules you don’t want to use the rate equation described here. You want to use the master equation, which was introduced in Part 4 of the network theory series. The difference between the two was explained in Part 2
The rate equation is only an approximation to the master equation, which is itself only an approximation to the actual laws of quantum mechanics governing chemistry, which are themselves only approximations to quantum field theory, etc.
Arjun Jain and I have a partially completed proof that the master equation reduces to the rate equation in a certain limit. I need to post that here! The remaining step in the proof is to rigorously justify passing a limit through a derivative.
I’m at most partly getting this (not your fault, it’s a great writeup:-), so the following question might not be sensible: The main theorem seems to imply that an arbitrary trajectory converges to an arbitrary strictly positive point of complex balance. But can’t there be many of the latter for a given system, and if so how can a fixed trajectory converge to all of them at once?
arch1 wrote:
It definitely doesn’t say or imply that—that’s the Global Attractor Conjecture, which is the biggest open question in reaction network theory! Manoj will talk about that more in his next post.
But you shouldn’t feel bad about making this slip, because Manoj said that some famous researchers in this subject made the same mistake. I forget the details—I hope he can tell us this story at some point.
In chemistry we have lots of conserved quantities, like the total amount of hydrogen, or oxygen, etc. Chemical reactions don’t change these. There is often one equilibrium for each choice of the values of these conserved quantities.
So, if we start with half a pound of hydrogen and two pounds of oxygen, we expect our chemical system to approach the equilibrium that has half a pound of hydrogen and two pounds of oxygen.
Taking these ideas and turning them into theorems—that’s where the fun starts. I suspect Manoj will also talk about this. But not everything we expect has been proved.
What John said :-)
Yes in fact Horn and Jackson also thought they had proved global convergence. This was the one small blemish in their otherwise extraordinary 1972 paper. Horn realized the mistake, and published a retraction two years later. We’ll see what the catch is next time. If you’re seen the autocatalysis post, then I can mention that it has to do with critical siphons.
Thanks John and Manoj!
A reaction network where every transition has just one species as input and one as output is the same as a continuous-time Markov chain, something like this:
We’ve got some finite set of states and a matrix
and a matrix  describing the probabilistic rate for a state to jump to the state
describing the probabilistic rate for a state to jump to the state  given that it’s in the state
given that it’s in the state 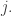 If the probability for the system to be found in any state is given by the distribution
If the probability for the system to be found in any state is given by the distribution
at time it evolves according to the master equation:
it evolves according to the master equation:
For probabilities to stay positive and for total probability to be conserved, we require that be infinitesimal stochastic, meaning that
be infinitesimal stochastic, meaning that
and
for all
When pondering ‘free energy’ and other thermodynamic notions for reaction networks, it’s good to start with this well-understood special case.
Kolmogorov came up with a criterion for a continuous-time Markov chain to be reversible. In the reversible case there exists an equilibrium state that obeys detailed balance. By equilibrium I simply mean that
that obeys detailed balance. By equilibrium I simply mean that  doesn’t change with time:
doesn’t change with time:
but detailed balance says more:
In other words, the probability per time for the state to hop from to
to  equals the probability per time for it to hop from
equals the probability per time for it to hop from  to
to 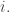
All this is just setting up notation and recalling standard stuff. Next I’ll bring in a concept from thermodynamics: namely, entropy!
Okay, suppose we have a reversible continuous-time Markov chain and is an equilibrium probability distribution obeying the detailed balance condition.
is an equilibrium probability distribution obeying the detailed balance condition.
To keep things simple, let’s also suppose the Markov chain is irreducible, so there’s just one equilibrium. (The general case can be broken up into irreducible pieces.)
In this situation every probability distribution q(t) will approach the equilibrium as it evolves in time according to the master equation:
as it evolves in time according to the master equation:
There are many Lyapunov functions, meaning functions of a probability distribution q(t) that always increase (or if you prefer to flip the sign, decrease) as time goes on:
of a probability distribution q(t) that always increase (or if you prefer to flip the sign, decrease) as time goes on:
and reach their maximum (or if you prefer, minimum) only at the equilibrium .
.
Many of these Lyapunov functions have been studied in detail. A systematic review is here:
• A. N. Gorban, P. A. Gorban and G. Judge, Entropy: the Markov ordering approach, Entropy 12 (2010), 1145–1193.
For example, when the equilibrium is a constant function, one of these Lyapunov functions is the Shannon entropy
is a constant function, one of these Lyapunov functions is the Shannon entropy
So, we get back the second law of thermodynamics!
But other Lyapunov functions give other ‘second laws’. For example, not only does Shannon entropy increase, so do all the Rényi entropies: these are a family of entropy functions which include Shannon entropy as a special case. I discussed this here:
• More second laws of thermodynamics, Azimuth.
When is not constant, we can reduce to the case where it is constant by a kind of transformation. So, all the formulas look a bit more fancy in this more general case, but the ideas are just the same. For example, instead of ordinary entropy being our Lyapunov function, we can use the relative entropy
is not constant, we can reduce to the case where it is constant by a kind of transformation. So, all the formulas look a bit more fancy in this more general case, but the ideas are just the same. For example, instead of ordinary entropy being our Lyapunov function, we can use the relative entropy
In other words:
Now, I claim that the decrease of free energy over time can be seen quite nicely in this general picture. However, it takes a little work!
After all, free energy is not quite the same as entropy. There’s a formula relating entropy, energy and free energy. But so far I haven’t brought energy into the picture. And this is what I want to do next. But it’s getting late, so I’ll stop here.
(I imagine plenty of experts know this whole story already. However, I’ve never seen it spelled out simply all in one place; I’ve been trying to pick it up here and there and assemble it all in my head. So, I feel the need to talk about it.)
So suppose we have a reversible continuous-time Markov chain and there’s a unique probability distribution obeying the detailed balance condition. This implies
obeying the detailed balance condition. This implies  is an equilibrium, but a lot more too, as described above.
is an equilibrium, but a lot more too, as described above.
Now let’s bring in energy. The idea is to pick a real number , the inverse temperature or coolness, and write the probabilities
, the inverse temperature or coolness, and write the probabilities  as a Boltzmann distribution, familiar from statistical mechanics:
as a Boltzmann distribution, familiar from statistical mechanics:
Here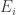 is a real number called the energy of the state
is a real number called the energy of the state  while
while 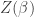 is a number chosen to make the probabilities sum to one, as they must:
is a number chosen to make the probabilities sum to one, as they must:
This number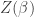 is called the partition function.
is called the partition function.
No matter what our probabilities are, and no matter what
are, and no matter what  we pick, we can find energies and a partition function that makes
we pick, we can find energies and a partition function that makes
The energies are not unique: we can add the same constant to all the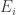 , and multiply
, and multiply 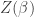 by some number, without changing the probabilities
by some number, without changing the probabilities 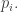 But this is the only ambiguity: the energies are well-defined up to an additive constant, which is what you expect in physics.
But this is the only ambiguity: the energies are well-defined up to an additive constant, which is what you expect in physics.
Speaking of ambiguities, our choice of inverse temperature was arbitrary as long as it’s not zero. If we multiply
was arbitrary as long as it’s not zero. If we multiply  by some number and divide all the energies by that same number, the numbers
by some number and divide all the energies by that same number, the numbers 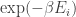 and thus the probabilities
and thus the probabilities  don’t change. This just says that our units of temperature are arbitrary as long as we correspondingly change our units of energy.
don’t change. This just says that our units of temperature are arbitrary as long as we correspondingly change our units of energy.
(I’m assuming Boltzmann’s constant is 1, so our units of temperature and units of energy are locked together.)
So, we’ve introduced concepts of energy and temperature into an arbitrary reversible continuous-time Markov chain that has a unique equilibrium obeying the detailed balance condition.
obeying the detailed balance condition.
In my last comment I introduced entropy. Given energy and entropy and temperature, we can define free energy. I’ll do that next.
Hmm, this may be more problematic than I thought, but let’s try.
In thermodynamics, free energy can be defined by
where is the expected energy,
is the expected energy,  is temperature and
is temperature and  is entropy.
is entropy.
Let’s say we’ve got a reversible continuous-time Markov chain that has a unique equilibrium probability distribution obeying the detailed balance condition. In this situation we can take any other probability distribution
obeying the detailed balance condition. In this situation we can take any other probability distribution  and try to compute its free energy using the formula above.
and try to compute its free energy using the formula above.
It’s straightforward to define the entropy of :
:
We can also compute its expected energy
where we define the energies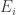 as in my previous comment, using
as in my previous comment, using
where
As mentioned earlier, these equations only define the energies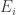 up to an additive constant. Since I can’t think of anything better to do, let’s choose that constant so that
up to an additive constant. Since I can’t think of anything better to do, let’s choose that constant so that  for our chosen inverse temperature
for our chosen inverse temperature  Then we have
Then we have
so
where the temperature is defined by
is defined by
Doing this, we get
so apparently the free energy of is
is
I say ‘apparently’ because the temperature has nothing intrinsic to do with
has nothing intrinsic to do with  ; it’s the temperature we arbitrarily assigned to the equilibrium state
; it’s the temperature we arbitrarily assigned to the equilibrium state 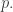
This makes me nervous, but at least we can do something now: we can compare this formula for free energy with the one Manoj gave in his post!
Manoj defined a concept of free energy for reaction networks by
Here is the set of species,
is the set of species,  is the number of items of items of species
is the number of items of items of species  in the complex balanced equilibrium
in the complex balanced equilibrium 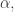 and
and 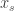 is the number of items of this species at some other point
is the number of items of this species at some other point 
A reaction network where every transition has just one species as input and one as output can be reintepreted as a continuous-time Markov chain. Translating to the Markov chain notation I’ve been using in previous comments, we get a concept of free energy
This is very similar to the quantity I called free energy in my last comment:
I claim they’re the same for all practical purposes. First, I introduced the constant in an ad hoc way, and it could be anything, so it would be fine to set
in an ad hoc way, and it could be anything, so it would be fine to set 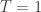 if all we want is some Lyapunov function. Then we get
if all we want is some Lyapunov function. Then we get
On the other hand, in our Markov process
is constant as a function of time: 1 if we treat the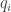 as probabilities, as I’ve been doing, or the total population of items, if we take the reaction network stance. Either way, it’s just some constant
as probabilities, as I’ve been doing, or the total population of items, if we take the reaction network stance. Either way, it’s just some constant  So,
So,
and thus
So, for a very special kind of reaction network, we’ve managed to use standard ideas from thermodynamics to understand the free energy function Manoj was discussing. And so it’s natural to try to generalize this argument to more reaction networks!
I won’t try the generalization to more general reaction networks now. I just want to mention another way to think about this free energy function for reversible Markov processes.
We’ve seen that setting the temperature to 1, we have
to 1, we have
But if we rewrite this as
we recognize it as the relative information of relative to
relative to  , or minus the relative entropy
, or minus the relative entropy
I’ve already mentioned that this is a Lyapunov function; now we’re seeing it in a somewhat new light!
Manoj, I can’t quite make sense of the proof of Lemma 4 unless I replace “We observe that this remainder flow satisfies the conditions of Lemma 4 on a graph with strictly fewer edges” with something like “We observe that *if* this remainder flow (on a graph with strictly fewer edges) satisfies the conditions of Lemma 4, then so does f.” Does the latter express your intended meaning, or am I confused?
@arch1 no, I think I said what I intended to say. Perhaps it will be helpful if I break things down further.
What do I mean by the conditions of Lemma 4? I mean that the remainder flow is conservative. That’s all! And that is easy to verify.
Now because the remainder flow is conservative, if Lemma 4 were true for the remainder flow, I would be done. But this process has reduced the problem of proving Lemma 4 to the problem of proving Lemma 4 on a smaller graph. Now I can apply infinite descent, which is a fancy name for mathematical induction run backwards.
Thanks Manoj, that helps!
[…] hat tip to the Azimuth Project and thanks to Manoj Gopalkrishnan for this interesting […]
First a disclaimer: I’m not sure how to post nice looking mathematics here.
I think it is worth noting that Martin Feinberg proved things in a different way than did Horn and Jackson. Marty posted some nice lecture notes (from a series of lectures in Wisconsin in 1979) that can be found at: http://crnt.engineering.osu.edu/LecturesOnReactionNetworks
In particular, his proof that the function being discussed here is, in fact, a Lyapunov function is quite nice. Let me redo it here as it is quite nice, though I will change the proof slightly by dropping the notion of “complex-space,” which Marty makes use of in his notes. I like this proof as it really shows (to me at least) where the complex balance condition comes in.
**********
Let be a deterministically modeled chemical reaction system with mass-action kinetics. Suppose that there are precisely
be a deterministically modeled chemical reaction system with mass-action kinetics. Suppose that there are precisely  species. We denote the
species. We denote the  th reaction by
th reaction by
and denote the span of the reaction vectors by
The ODE governing the dynamics of the system is
Assume that the system is complex-balanced with complex-balanced equilibrium . This means that for each
. This means that for each  ,
,
where the sum on the left is over all reactions for which is the source complex, and the sum on the right is over all reactions for which
is the source complex, and the sum on the right is over all reactions for which  is the product complex.
is the product complex.
Now define the function by
by
The fact that is a Lyapunov function for the system is captured in the following result.
is a Lyapunov function for the system is captured in the following result.
Theorem. Suppose that with
with 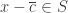 . Then
. Then
with equality if and only if .
.
Proof. Note that
Using that for any real numbers we have
we have 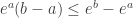 with equality if and only if
with equality if and only if 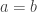 (consider secant lines of
(consider secant lines of 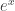 ), we have
), we have
where the final equality holds by the condition above on complex-balancing.
Thus, we have a strict inequality unless
for all . That is, we have a strict inequality unless
. That is, we have a strict inequality unless
Following precisely the argument on page 4–33 of Feinberg’s notes, we now note that if both
and
hold, then
which, by the monotonicity of the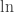 function, can only happen if
function, can only happen if  for all
for all  .
.
That’s a very nice proof, I had not seen it before. Thanks!
Oh dear, that did not work. I have simply posted the note here:
Click to access CRNT_Lyapunov.pdf
I’ve fixed the LaTeX in your comment, but it’s nice to have a PDF version too.
I’m glad to see you here! We’ve spent a lot of time here discussing your work on stationary solutions of the master equation for complex-balanced systems.
Thanks for posting this comment! It’s great to see another proof of this important result.
For more remarks comparing different paper on Lyapunov functions for chemical reaction networks and evolutionary games, go here. I will try to summarize all these ideas in a blog post at some point, but right now we’ve got two parallel conversations going on: one featuring chemical reaction network theorists and one featuring evolutionary game theorists… both talking about free energy as a Lyapunov function.
Now Tobias Fritz and I have finally finished our paper on this subject:
• A Bayesian characterization of relative entropy.
Here’s a great paper on Lyapunov functions for Markov processes and chemical reaction networks:
• Alexander N. Gorban, General H-theorem and entropies that violate the second law, Entropy 16 (2014), 2408–2432.
Indeed John, some very exciting ideas that are new to me in this paper! In particular, towards the end he has worked out a challenge example that Anne Shiu, Ezra Miller and I set out in our paper arXiv:1305.5303. I hope to read it thoroughly and write more about it in my next blog entry. Sorry it’s taking so long to get done.
Manoj Gopalkrishnan, who has written a couple of great posts on chemical reaction networks here on Azimuth, is talking about a way to do statistical inference with chemical reactions. His talk is called ‘Statistical inference with a chemical soup’.