Here in Copenhagen we’ll soon be having a bunch of interesting talks on chemical reaction networks:
• Workshop on Mathematical Trends in Reaction Network Theory, 1-3 July 2015, Department of Mathematical Sciences, University of Copenhagen. Organized by Elisenda Feliu and Carsten Wiuf.
Looking through the abstracts, here are a couple that strike me.
First of all, Gheorghe Craciun claims to have proved the biggest open conjecture in this field: the Global Attractor Conjecture!
• Gheorge Craciun, Toric differential inclusions and a proof of the global attractor conjecture.
This famous old conjecture says that for a certain class of chemical reactions, the ones coming from ‘complex balanced reaction networks’, the chemicals will approach equilibrium no matter what their initial concentrations are. Here’s what Craciun says:
Abstract. In a groundbreaking 1972 paper Fritz Horn and Roy Jackson showed that a complex balanced mass-action system must have a unique locally stable equilibrium within any compatibility class. In 1974 Horn conjectured that this equilibrium is a global attractor, i.e., all solutions in the same compatibility class must converge to this equilibrium. Later, this claim was called the Global Attractor Conjecture, and it was shown that it has remarkable implications for the dynamics of large classes of polynomial and power-law dynamical systems, even if they are not derived from mass-action kinetics. Several special cases of this conjecture have been proved during the last decade. We describe a proof of the conjecture in full generality. In particular, it will follow that all detailed balanced mass action systems and all deficiency zero mass-action systems have the global attractor property. We will also discuss some implications for biochemical mechanisms that implement noise filtering and cellular homeostasis.
Manoj Gopalkrishnan wrote a great post explaining the concept of complex balanced reaction network here on Azimuth, so if you want to understand the conjecture you could start there.
Even better, Manoj is talking here about a way to do statistical inference with chemistry! His talk is called ‘Statistical inference with a chemical soup’:
Abstract. The goal is to design an “intelligent chemical soup” that can do statistical inference. This may have niche technological applications in medicine and biological research, as well as provide fundamental insight into the workings of biochemical reaction pathways. As a first step towards our goal, we describe a scheme that exploits the remarkable mathematical similarity between log-linear models in statistics and chemical reaction networks. We present a simple scheme that encodes the information in a log-linear model as a chemical reaction network. Observed data is encoded as initial concentrations, and the equilibria of the corresponding mass-action system yield the maximum likelihood estimators. The simplicity of our scheme suggests that molecular environments, especially within cells, may be particularly well suited to performing statistical computations.
It’s based on this paper:
• Manoj Gopalkrishnan, A scheme for molecular computation of maximum likelihood estimators for log-linear models.
I’m not sure, but this idea may exploit existing analogies between the approach to equilibrium in chemistry, the approach to equilibrium in evolutionary game theory, and statistical inference. You may have read Marc Harper’s post about that stuff!
David Doty is giving a broader review of ‘Computation by (not about) chemistry’:
Abstract. The model of chemical reaction networks (CRNs) is extensively used throughout the natural sciences as a descriptive language for existing chemicals. If we instead think of CRNs as a programming language for describing artificially engineered chemicals, what sorts of computations are possible for these chemicals to achieve? The answer depends crucially on several formal choices:
1) Do we treat matter as infinitely divisible (real-valued concentrations) or atomic (integer-valued counts)?
2) How do we represent the input and output of the computation (e.g., Boolean presence or absence of species, positive numbers directly represented by counts/concentrations, positive and negative numbers represented indirectly by the difference between counts/concentrations of a pair of species)?
3) Do we assume mass-action rate laws (reaction rates proportional to reactant counts/concentrations) or do we insist the system works correctly under a broader class of rate laws?
The talk will survey several recent results and techniques. A primary goal of the talk is to convey the “programming perspective”: rather than asking “What does chemistry do?”, we want to understand “What could chemistry do?” as well as “What can chemistry provably not do?”
I’m really interested in chemical reaction networks that appear in biological systems, and there will be lots of talks about that. For example, Ovidiu Radulescu will talk about ‘Taming the complexity of biochemical networks through model reduction and tropical geometry’. Model reduction is the process of simplifying complicated models while preserving at least some of their good features. Tropical geometry is a cool version of algebraic geometry that uses the real numbers with minimization as addition and addition as multiplication. This number system underlies the principle of least action, or the principle of maximum energy. Here is Radulescu’s abstract:
Abstract. Biochemical networks are used as models of cellular physiology with diverse applications in biology and medicine. In the absence of objective criteria to detect essential features and prune secondary details, networks generated from data are too big and therefore out of the applicability of many mathematical tools for studying their dynamics and behavior under perturbations. However, under circumstances that we can generically denote by multi-scaleness, large biochemical networks can be approximated by smaller and simpler networks. Model reduction is a way to find these simpler models that can be more easily analyzed. We discuss several model reduction methods for biochemical networks with polynomial or rational rate functions and propose as their common denominator the notion of tropical equilibration, meaning finite intersection of tropical varieties in algebraic geometry. Using tropical methods, one can strongly reduce the number of variables and parameters of biochemical network. For multi-scale networks, these reductions are computed symbolically on orders of magnitude of parameters and variables, and are valid in wide domains of parameter and phase spaces.
I’m talking about the analogy between probabilities and quantum amplitudes, and how this makes chemistry analogous to particle physics. You can see two versions of my talk here, but I’ll be giving the ‘more advanced’ version, which is new:
• Probabilities versus amplitudes.
Abstract. Some ideas from quantum theory are just beginning to percolate back to classical probability theory. For example, the master equation for a chemical reaction network describes the interactions of molecules in a stochastic rather than quantum way. If we look at it from the perspective of quantum theory, this formalism turns out to involve creation and annihilation operators, coherent states and other well-known ideas—but with a few big differences.
Anyway, there are a lot more talks, but if I don’t have breakfast and walk over to the math department, I’ll miss those talks!
You can learn more about individual talks in the comments here (see below) and also in Matteo Polettini’s blog:
• Matteo Polettini, Mathematical trends in reaction network theory: part 1 and part 2, Out of Equilibrium, 1 July 2015.
Azimuth 
I’m watching the first talk, Sebastian Walcher on ‘Computational aspects of quasi-steady state reduction’.
The first big problem is defining ‘quasi-steady state’. The idea is to simplify (bio-)chemical reaction networks by separating them into fast and slow parts. There were 2 approaches: separating them into fast and slow species, or fast and slow reactions.
He is treating it as a singular perturbation problem.
Let’s consider a parameter-dependent ODE
where
is a parameter. Then Tikhonov’s theorem takes care of the system when we have a ‘small parameter’ and separation into slow and fast coordinates. But how do we find this separation?
Example: consider the Michaelis-Menten model of an enzyme
binding to a substrate 
and forming a complex 
and then forming a product 
:
made a bit fancier than usual by allowing the second reaction to be reversible.
Michaelis and Menten (1913) assumed instantaneous substrate-complex equilibrium: the second reaction goes a lot faster than the reverse first reaction.
Briggs and Haldane (1925) assumed stationary complex concentration:
small.
This problem is already worth a lot of thought.
One goal in this game is to take a chemical reaction network and find all ways of finding a ‘slow manifold’—a subset of concentrations where all reactions occur ‘slowly’, such that the fast reactions carry the concentrations toward this slow manifold. We can then use perturbation theory to study the behavior of the system near the slow manifold.
Somewhat to my surprise, one of the proofs used the Tarski-Seidenberg theorem, which lies at the interface of semialgebraic geometry and logic.
Namely: if we take a set in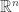
defined by polynomial equations and inequalities, and we project it down onto 
the resulting set is still definable in terms of polynomial identities and inequalities!
(Semialgebraic geometry is where we get to use inequalities along with polynomials to define sets, just as in algebraic geometry we get to use equations involving polynomials.)
[…] I’ll try to live-blog my notes from this very interesting conference, knowing that I can hardly compete with Azimuth… […]
Hi there, Matteo! We’re not competing, we’re cooperating! I’m glad to see your notes on this workshop, which seem to pick up just where mine leave off.
Georghe Craciun is now talking about his claimed proof of the following big conjecture!
Theorem (Horn–Jackson, 1972). If a reaction network is complex balanced then there exists a strict Lyapunov function within each linear invariant subspace.
Conjecture (Horn, 1974) If a reaction network is complex balanced then there exists a globally attracting point within each linear invariant subspace.
Craciun is taking a very geometrical approach where he draws a graph with straight edges in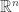
for any chemical reaction network with 
species. A reaction carrying the complex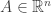 
to the complex 
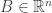gives an edge 
He notes that if such a graph is weakly reversible and in general position, then it’s complex balanced: if there’s an edge going into a point in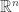 
there’s an edge going out, and vice versa.
If you have a strict Lyapunov function you might think it’s automatic to get a unique global attractor. The problem is that the system can run off to the ‘boundary’, where the concentration of one or more species vanishes. If we can rule this out then there must be a unique global attractor!
So, we say we need to prove ‘persistence’: no species go away.
Main results of Craciun’s paper:
Theorem A. If a polynomial dynamical system can be represented by a weakly reversible chemical reaction network, then it can be embedded in a toric differential inclusion.
Theorem B. Toric differential inclusions have an exhaustive set of zero-separating surfaces.
Theorem C. Complex balanced systems are persistent.
which by previous work shows
Thoerem D. Complex balanced systems have a unique global attractor within each linear invariant subspace.
I asked Georghe how much fancy stuff about toric geometry he used in his proof, and he laughed and said none.
Georg Regensburger is talking about ‘Parametrizing complex balancing equilibria of generalized mass-action systems’.
He’s pointing out the relation between complex balanced equilibria and kernels of graph Laplacians, which reminds me of the theorem in Part 23 of the network theory series. I think more on this can be found here:
• Karin Gatermann and M. Wolfrum, Bernstein’s second theorem and Viro’s method for sparse polynomial systems in chemistry.
and in other papers by Karin Gatermann.
He can use this to parametrize all complex balanced equilibria of a reaction network, even for a class of systems that doesn’t obey the law of mass action, but instead a generalization thereof.
The paper:
Stefan Müller and Georg Regensburger, Generalized mass-action systems and positive solutions of polynomial equations with real and symbolic exponents.
Now Shodan Rao is giving a talk called ‘Complex and detailed balancing of chemical reaction networks revisited’. This may be based on
• Arjan van der Schaft, Shodhan Rao and Bayu Jayawardhana, On the mathematical structure of balanced chemical reaction networks governed by mass action kinetics.
An issue of terminology: what I call the Kolmogorov condition for detailed balance is called the Wegscheider condition when it’s applied to chemical reaction networks.
Namiko Mitarai at the Center of Models of Life (in Copenhagen) is talking about ‘Emergence of diversity in a model ecosystem’. Unlike most of the talks in this workshop, she’s using a spatial model.
If you have the Java runtime environment enabled (which the powers that be are making ever more difficult, due to security concerns), you can see an applet that runs Mitarai’s program:
• Namiko Mitarai, Ecosystems with mutually exclusive interactions self-organize to a state of high diversity.
You can install the Java runtime environment here, and enable it by following the directions here.
She began by showing some matrices that describe how often one species is observed to invade another, e.g. in the case of lichen growing on rock.
Her program tries to explain how this works. It runs a simple lattice model that shows a transition between low-diversity and high-diversity states.
Consider a square lattice with
states with each site carrying an individual of one species. Suppose we have a random matrix of 0s and 1s, 
saying which species can invade which other species. The entries of this matrix are chosen randomly and independently with probability 
of being 1.
At each step, randomly choose a site and a neighbor. The species
at the first site ‘invades’ and replaces the species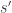 
in the neighboring site if 
Also, with some small rate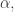
a new species tries to invade a randomly chosen site. When this happens we need to increase the size of our matrix, randomly choosing 0s and 1s in a new row and new column. The matrix entries are used to decide if the invasion succeeds, in the usual way.
When
the mean field approximation obeys a standard Lotka–Volterra equation.
For large
we tend to have fewer species after a long time. The decline becomes discontinuous in the limit 
For values of 
slightly above the phase transition there’s bistable hopping between high-diversity and low-diversity states. For values of 
below the transition there is always high diversity.
Hello, I am one of the participants of the workshop! I really found your talk interesting. I have been thinking about it, particularly after Namiko Mitarai’s talk.
My impression is, her model is quite field theoretic. Colorful territories reminded me Ising (or Potts) model.
Besides, each lattice only admits one species. I thought this could be modeled by fermion…
Anyway, whether or not my idea is useful to describe her model, have you ever considered fermionic system, in your analogy? If you do, then could you give us some notes and readings in your blog or somewhere?
Below I would like to summarize what I have in mind.
Now the spectrum of the number operator for fermions is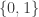
. Fock space may be constructed if you introduce Grassmann number. An element 
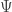of the Fock space with 
species should look like
Creation and annihilation operators are of course multiplications and derivatives, and they satisfy anticommutation relation:
Now I have some troubles in constructing Hamiltonian and a master equation. Because I am using Grassmann number, for example the direct analogy
does not seem to work…
I would be happy if you could give me any comments on these things!
People have thought about using fermionic quantum field field theories to describe stochastic systems where we can have at most one entity per site. I don’t know the best references, but here is one:
• Vivien Brunel, Klaus Oerding and Frédéric van Wijland, Fermionic field theory for directed percolation in (1 + 1)-dimensions, J. Phys. A: Math. Gen. 33 (2000) 1085–1097.
I hope you’re familiar with the use of bosonic quantum field theory to study reaction-diffusion models, e.g. reviewed here:
• Johannes Knebel, Application of Statistical Field Theory to Reaction-Diffusion Problems, 29 April 2010.
Tat Dat Tran is talking about ‘A connection between population gnetics and chemical reaction networks’. An example is the reaction network
which gives the Moran model of population genetics. It’s complex balanced, so we can understand it in detail. He uses the Kullback–Leibler divergence as a Lyapunov function for the rate equation. He uses the Anderson–Craciun–Kurtz theorem to get stationary distributions for the master equation.
His talk is reminding me that I should read this paper:
• David F. Anderson, Gheorghe Craciun, Manoj Gopalkrishnan and Carsten Wiuf, Lyapunov functions, stationary distributions, and non-equilibrium potential for chemical reaction networks.
Does your “probabilities versus amplitudes” somehow “square” with the Geometrical Formulation of Quantum Mechanics by Ashtekar-Schilling? http://arxiv.org/abs/gr-qc/9706069 (I just discovered this via the late comment to your Classical Mechanics versus Thermodynamics blog.)
(Sorry, I don’t have HTML-angles on this hilariously stupid “netbook” I’m using.)
I love that stuff about the geometrical formulation of quantum mechanics, and I have an unfinished draft of a paper about it somewhere on my computer. I may never finish it. The way I see it, the ‘geometric quantization’ functor from Kähler manifolds to Hilbert spaces has a kind of adjoint sending each Hilbert space to its corresponding projective space (the space of quantum states), which is a Kähler manifold.
However, I know of no relation between this circle of ideas and the funny analogy between probabilities and amplitudes that my talk was about.
That analogy really amounts to
and I like to joke that the next revolution in physics will involve L3 spaces.
(I don’t believe that: it’s just a joke, though you should look at Smolin’s paper.)
Ovidiu Radulescu is talking about “Taming the complexity of biochemical networks through model reduction and tropical geometry.”
The reaction networks in biology are too big for efficient parameter estimation, so we want to use model reduction to simplify them, e.g. lumping together several ‘fast’ reactions into a single reaction. But there aren’t just two time scales, fast and slow—there are many time scales, differing by several orders of magnitude.
In 2008 Gorban and Radulescu looked at ‘monomolecular’ reaction networks, which are really just Markov processes, with rate constants equal to
where the reaction 
is labelled by an integer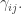 
In other words, time scales are integer powers of a time scale
• A. N. Gorban and O. Radulescu, Dynamic and static limitation in reaction networks, revisited, Advances in Chemical Engineering 34 (2008), 103–173.
They consider 4 rules for simplifying such graphs. For example, if you ‘prune’ edges labelled by larger integers, that means you’re ignoring slower reactions. You can ‘pool’ nodes connected by smaller integers, meaning that if some species rapidly turn into each other you can treat them as a single species.
Theorem. The multiscale approximation of an arbitrary Markov process with rate constants
is a Markov process of this sort without loops and without more than one edge leaving any node.
Things get more tricky for full-fledged reaction networks, since then concentrations can affect reaction rates. The fast variables move to equilibrium taking us to a ‘slow submanifold’ where only the slow variables matter, but in a multiscale problem this can happen repeatedly at different time scales. See Chiavazzo e al in Comm. Comp. Phys. 2007.
How can we determine the slow/fast decomposition? See:
• O. Radulescu, A. N. Gorban, A. Zinovyev and A. Lilienbaum, Robust simplifications of multiscale biochemical networks, BMC Systems Biology 2 (2008).
The model reduction procedure: Prune fast species, replace fast sub-systems by elementary modes (reaction pooling).
For fast cycles you get certain quantities conserved by the fast reactions, but which change slowly since they’re not conserved by all reactions.
‘Elementary modes’ and ‘approximate conserved quantities’ are a way to take the degrees of freedom of a subsystem and split them into the rapidly changing ones and the slowly changing ones. Ideally only the slowly changing ones are coupled to the environment.
Irene Otero-Muras is talking about ‘Chemical Reaction Network Theory (CRNT) insights to improve parameter identifiability in biochemical reaction network models.’
It’s always hard to understand the structure of chemical reaction networks in biology, and also the parameters (rate constants).
Luckily there are some theorems that help us understand structure: certain networks can’t exhibit certain behavior regardless of their rate constants.
She’s going to talk about estimating rate constants for networks that exhibit bistability.
Her talk is based on this paper:
• Irene Otero-Muras, Julio R. Banga and Antonio A. Alonso, Characterizing multistationarity regimes in biochemical reaction networks, PLOS One, 3 July 2012.
The idea is to look at steady state concentrations of one chemical as functions of some stimulus, and find bifurcations. These look like the usual ‘cusp catastrophe’ of René Thom fame. The location of the catastrophe helps determine the rate constants.
She consider this reaction network, the Edelstein network, which is famous for exhibiting bistability:
Now Daniele Cappelletti is speaking on a subject dear to my heart, ‘Complex balanced reaction systems and product-form Poisson distributions’.
The rough idea is to treat the existence of a stationary state for the master equation that’s a product of Poisson distributions as analogous to the ‘complex balanced’ condition for the rate equation.
He has a lot of nice theorems on this with Carsten Wiuf, which unfortunately went by too fast for me to type them in! Their paper is not yet on the arXiv.
Matteo Polettini is speaking about ‘Chemical networks and their topology: a thermodynamic perspective’.
He says “my personal obsession is with cycles”.
“Thermodynamics is all about cycles and how they couple.”
How do you make sense of an open chemical reaction network with ‘chemostats’ holding the concentration of certain species constant.
If the deficiency of a reaction network is zero, stochastic dissipation = deterministic dissipation.
The detailed balance condition prevents water from flowing around in a loop without some outside source. To get around this problem, we need to consider metabolic networks as open chemical reaciton networks.
For a closed network, we have the Wegscheider or Kolmogorov condition: the product of rates around a cycle equals the product of the rates around the reverse cycle. The ratio of forward and backwards rates along an edge
can be used to define the change of free energy along that edge:
Summing this around a loop gives zero.
The sum of these quantities weighted by the flows along the edges is zero in an equilibrium state… for a closed network.
If we fix concentrations of certain species (using “chemostats”), we get emergent cycles that can violate the Wegscheider or Kolmogorov condition.
• Matteo Polettini and Massimiliano Esposito, Irreversible thermodynamics of open chemical networks I: Emergent cycles and broken conservation laws.
This reaction network has no ‘visible’ cycles–no cycles in the graph. However, it gives a cycle in the space of species. This can only happen when our reaction network has nonzero deficiency.
There’s a ‘rate of entropy production’ due to Schnakenberg 1976. We can do a calculation to show it’s nonnegative, and it’s the entropy flow to the environment minus the entropy production within the system. In a steady state, the latter term vanishes.
In the deficiency zero case we can carry out a more detailed analysis:
• Matteo Polettini, Artur Wachtel and Massimiliano Esposito, Dissipation in noisy chemical networks: the role of deficiency.
I didn’t realize you kept posting in the comment session…
That makes it a bit easier to keep posting small bits of information.
Alan Rendall is someone I know from the old days when we were both working on problems related to quantum gravity. Like me he’s now interested in biology, and just spoke about models of the ‘mitogen-activated protein kinase cascade‘ or MAPK.
MAPKs help cells in your body respond to a diverse array of stimuli. In a blog article, Rendall writes:
Indeed, Alan’s talk reviewed a lot of interesting questions related to multistationarity, bistability and ‘biological clocks’ that show up chemical reaction network models of the MAP kinase cascade—and a lot of interesting answers, comingfrom both rigorous theorems and simulations.
You can see some of his work here:
• Alan Rendall and Juliette Hell, A proof of bistability for the dual futile cycle.
The dual futile cycle is this reaction network, which shows up as part of the MAP kinase cascade:
It’s called ‘futile’ because the phosphate groups, the P’s, get first added with the help of an enzyme E and then taken away with the help of an enzyme F. In this example we have at most two P’s, but we could have more. Then we’d have a multiple futile cycle.
In his paper Rendall writes:
There’s more in two papers of theirs that aren’t out yet, ‘Sustained oscillations in the MAPK cascade’ and ‘Dynamical features of the MAPK cascade’, and more on his blog:
• Alan Rendall, Dynamics of the MAP kinase cascade, Hydrobates, 7 April 2012.
• Alan Rendall, Proofs of dynamical properties of the MAPK cascade, Hydrobates, 3 April 2014.
The first one is the one I quoted.
David Anderson is going to focus on reaction networks with a deficiency of one, going beyond the standard deficiency-zero story. In particular, he’ll talk about so-called ‘absolute concentration robustness’ models, introduced by Feinberg and Shinar in 2010, in one of the few papers in Science where the main result is a theorem:
• Martin Feinberg and Guy Shinar, Structural sources of robustness in biochemical reaction networks, Science 327 (2010), 1389–1391.
You can see a version of David’s talk here:
• David Anderson, Stochastic models of biochemical reaction systems: network structure and qualitative dynamics, 17 April 2015.
If you’re missing the prerequisites, start here:
• David Anderson, Tutorial: stochastic models of biochemical reaction systems, 16 April 2015.
His talk is based on this paper:
• David F. Anderson, Germán Enciso, and Matthew D. Johnston, Stochastic analysis of biochemical reaction networks with absolute concentration robustness, Journal of the Royal Society Interface, 11 (2014), 20130943.
Example:
has absolute concentration robustness in
, because this species has the same equilibrium value, regardless of initial conditions!
There are much more complicated models with this property, as shown in the paper by Feinberg and Shinar.
The theorem says: suppose you have a reaction network with a deficiency of one that admits a positive steady state. If, in the network, there are two nonterminal nodes that differ only in species S, then the system has absolute concentration robustness in S.
Amazing!
(In the above example the nodes
and 
are nonterminal, since they have arrows pointing out of them, and they differ in one species.)
This result of Feinberg and Shinar applies to the rate equation. Anderson’s work says what the master equation says about the same situation!
If you put yeast cells in water containing a constant low concentration of glucose, they convert it into alcohol at a constant rate. But if you increase the concentration of glucose something funny happens. The alcohol output starts to oscillate!
It’s not that the yeast is doing something clever and complicated. If you break down the yeast cells, killing them, this effect still happens. People think these oscillations are inherent to the chemical reactions in glycolysis.
I learned this after writing Part 1, thanks to Alan Rendall. I first met Alan when we were both working on quantum gravity. But last summer I met him in Copenhagen, where we both attending the workshop Trends in reaction network theory. It turned out that now he’s deep into the mathematics of biochemistry, especially chemical oscillations!
There’s a workshop this summer:
• Dynamics, Thermodynamics and Information Processing in Chemical Networks, 13-16 June 2017, Complex Systems and Statistical Mechanics Group, University of Luxembourg. Organized by Massimiliano Esposito and Matteo Polettini.
They write, “The idea of the workshop is to bring in contact a small number of high-profile research groups working at the frontier between physics and biochemistry, with particular emphasis on the role of Chemical Networks.”
I’m looking forward to this, in part because there will be a mix of speakers I’ve met, speakers I know but haven’t met, and speakers I don’t know yet. I feel like reminiscing a bit, and I hope you’ll forgive me these reminiscences, since if you try the links you’ll get an introduction to the interface between computation and chemical reaction networks.