Here you see three planets. The blue planet is orbiting the Sun in a realistic way: it’s going around an ellipse.
The other two are moving in and out just like the blue planet, so they all stay on the same circle. But they’re moving around this circle at different rates! The green planet is moving faster than the blue one: it completes 3 orbits each time the blue planet goes around once. The red planet isn’t going around at all: it only moves in and out.
What’s going on here?
In 1687, Isaac Newton published his Principia Mathematica. This book is famous, but in Propositions 43–45 of Book I he did something that people didn’t talk about much—until recently. He figured out what extra force, besides gravity, would make a planet move like one of these weird other planets. It turns out an extra force obeying an inverse cube law will do the job!
Let me make this more precise. We’re only interested in ‘central forces’ here. A central force is one that only pushes a particle towards or away from some chosen point, and only depends on the particle’s distance from that point. In Newton’s theory, gravity is a central force obeying an inverse square law:
for some constant But he considered adding an extra central force obeying an inverse cube law:
He showed that if you do this, for any motion of a particle in the force of gravity you can find a motion of a particle in gravity plus this extra force, where the distance is the same, but the angle
is not.
In fact Newton did more. He showed that if we start with any central force, adding an inverse cube force has this effect.
There’s a very long page about this on Wikipedia:
• Newton’s theorem of revolving orbits, Wikipedia.
I haven’t fully understood all of this, but it instantly makes me think of three other things I know about the inverse cube force law, which are probably related. So maybe you can help me figure out the relationship.
The first, and simplest, is this. Suppose we have a particle in a central force. It will move in a plane, so we can use polar coordinates to describe its position. We can describe the force away from the origin as a function
Then the radial part of the particle’s motion obeys this equation:
where is the magnitude of particle’s angular momentum.
So, angular momentum acts to provide a ‘fictitious force’ pushing the particle out, which one might call the centrifugal force. And this force obeys an inverse cube force law!
Furthermore, thanks to the formula above, it’s pretty obvious that if you change but also add a precisely compensating inverse cube force, the value of
will be unchanged! So, we can set things up so that the particle’s radial motion will be unchanged. But its angular motion will be different, since it has a different angular momentum. This explains Newton’s observation.
It’s often handy to write a central force in terms of a potential:
Then we can make up an extra potential responsible for the centrifugal force, and combine it with the actual potential into a so-called effective potential:
The particle’s radial motion then obeys a simple equation:
For a particle in gravity, where the force obeys an inverse square law and is proportional to
the effective potential might look like this:

This is the graph of
If you’re used to particles rolling around in potentials, you can easily see that a particle with not too much energy will move back and forth, never making it to or
This corresponds to an elliptical orbit. Give it more energy and the particle can escape to infinity, but it will never hit the origin. The repulsive ‘centrifugal force’ always overwhelms the attraction of gravity near the origin, at least if the angular momentum is nonzero.
On the other hand, suppose we have a particle moving in an attractive inverse cube force! Then the potential is proportional to so the effective potential is
where is negative for an attractive force. If this attractive force is big enough, namely
then this force can exceed the centrifugal force, and the particle can fall in to
If we keep track of the angular coordinate we can see what’s really going on. The particle is spiraling in to its doom, hitting the origin in a finite amount of time!
This should remind you of a black hole, and indeed something similar happens there, but even more drastic:
• Schwarzschild geodesics: effective radial potential energy, Wikipedia.
For a nonrotating uncharged black hole, the effective potential has three terms. Like Newtonian gravity it has an attractive term and a repulsive
term. But it also has an attractive term
term! In other words, it’s as if on top of Newtonian gravity, we had another attractive force obeying an inverse fourth power law! This overwhelms the others at short distances, so if you get too close to a black hole, you spiral in to your doom.
For example, a black hole can have an effective potential like this:

But back to inverse cube force laws! I know two more things about them. A while back I discussed how a particle in an inverse square force can be reinterpreted as a harmonic oscillator:
• Planets in the fourth dimension, Azimuth.
There are many ways to think about this, and apparently the idea in some form goes all the way back to Newton! It involves a sneaky way to take a particle in a potential
and think of it as moving around in the complex plane. Then if you square its position—thought of as a complex number—and cleverly reparametrize time, you get a particle moving in a potential
This amazing trick can be generalized! A particle in a potential
can transformed to a particle in a potential
if
A good description is here:
• Rachel W. Hall and Krešimir Josić, Planetary motion and the duality of force laws, SIAM Review 42 (2000), 115–124.
This trick transforms particles in potentials with
ranging between
and
to
potentials with
ranging between
and
It’s like a see-saw: when
is small,
is big, and vice versa.
But you’ll notice this trick doesn’t actually work at the case that corresponds to the inverse cube force law. The problem is that
in this case, so we can’t find
with
So, the inverse cube force is special in three ways: it’s the one that you can add on to any force to get solutions with the same radial motion but different angular motion, it’s the one that naturally describes the ‘centrifugal force’, and it’s the one that doesn’t have a partner! We’ve seen how the first two ways are secretly the same. I don’t know about the third, but I’m hopeful.
Quantum aspects
Finally, here’s a fourth way in which the inverse cube law is special. This shows up most visibly in quantum mechanics… and this is what got me interested in this business in the first place.
You see, I’m writing a paper called ‘Struggles with the continuum’, which discusses problems in analysis that arise when you try to make some of our favorite theories of physics make sense. The inverse square force law poses interesting problems of this sort, which I plan to discuss. But I started wanting to compare the inverse cube force law, just so people can see things that go wrong in this case, and not take our successes with the inverse square law for granted.
Unfortunately a huge digression on the inverse cube force law would be out of place in that paper. So, I’m offloading some of that material to here.
In quantum mechanics, a particle moving in an inverse cube force law has a Hamiltonian like this:
The first term describes the kinetic energy, while the second describes the potential energy. I’m setting and
to remove some clutter that doesn’t really affect the key issues.
To see how strange this Hamiltonian is, let me compare an easier case. If the Hamiltonian
is essentially self-adjoint on which is the space of compactly supported smooth functions on 3d Euclidean space minus the origin. What this means is that first of all,
is defined on this domain: it maps functions in this domain to functions in
. But more importantly, it means we can uniquely extend
from this domain to a self-adjoint operator on some larger domain. In quantum physics, we want our Hamiltonians to be self-adjoint. So, this fact is good.
Proving this fact is fairly hard! It uses something called the Kato–Lax–Milgram–Nelson theorem together with this beautiful inequality:
for any
If you think hard, you can see this inequality is actually a fact about the quantum mechanics of the inverse cube law! It says that if the energy of a quantum particle in the potential
is bounded below. And in a sense, this inequality is optimal: if
, the energy is not bounded below. This is the quantum version of how a classical particle can spiral in to its doom in an attractive inverse cube law, if it doesn’t have enough angular momentum. But it’s subtly and mysteriously different.
You may wonder how this inequality is used to prove good things about potentials that are ‘less singular’ than the potential: that is, potentials
with
For that, you have to use some tricks that I don’t want to explain here. I also don’t want to prove this inequality, or explain why its optimal! You can find most of this in some old course notes of mine:
• John Baez, Quantum Theory and Analysis, 1989.
See especially section 15.
But it’s pretty easy to see how this inequality implies things about the expected energy of a quantum particle in the potential . So let’s do that.
In this potential, the expected energy of a state is:
Doing an integration by parts, this gives:
The inequality I showed you says precisely that when this is greater than or equal to zero. So, the expected energy is actually nonnegative in this case! And making
greater than
only makes the expected energy bigger.
Note that in classical mechanics, the energy of a particle in this potential ceases to be bounded below as soon as Quantum mechanics is different because of the uncertainty principle! To get a lot of negative potential energy, the particle’s wavefunction must be squished near the origin, but that gives it kinetic energy.
It turns out that the Hamiltonian for a quantum particle in an inverse cube force law has exquisitely subtle and tricky behavior. Many people have written about it, running into ‘paradoxes’ when they weren’t careful enough. Only rather recently have things been straightened out.
For starters, the Hamiltonian for this kind of particle
has different behaviors depending on Obviously the force is attractive when
and repulsive when
but that’s not the only thing that matters! Here’s a summary:
• In this case
is essentially self-adjoint on
So, it admits a unique self-adjoint extension and there’s no ambiguity about this case.
• In this case
is not essentially self-adjoint on
In fact, it admits more than one self-adjoint extension! This means that we need extra input from physics to choose the Hamiltonian in this case. It turns out that we need to say what happens when the particle hits the singularity at
This is a long and fascinating story that I just learned yesterday.
• In this case the expected energy
is bounded below for
It turns out that whenever we have a Hamiltonian that is bounded below, even if there is not a unique self-adjoint extension, there exists a canonical ‘best choice’ of self-adjoint extension, called the Friedrichs extension. I explain this in my course notes.
• In this case the expected energy is not bounded below, so we don’t have the Friedrichs extension to help us choose which self-adjoint extension is ‘best’.
To go all the way down this rabbit hole, I recommend these two papers:
• Sarang Gopalakrishnan, Self-Adjointness and the Renormalization of Singular Potentials, B.A. Thesis, Amherst College.
• D. M. Gitman, I. V. Tyutin and B. L. Voronov, Self-adjoint extensions and spectral analysis in the Calogero problem, Jour. Phys. A 43 (2010), 145205.
The first is good for a broad overview of problems associated to singular potentials such as the inverse cube force law; there is attention to mathematical rigor the focus is on physical insight. The second is good if you want—as I wanted—to really get to the bottom of the inverse cube force law in quantum mechanics. Both have lots of references.
Also, both point out a crucial fact I haven’t mentioned yet: in quantum mechanics the inverse cube force law is special because, naively, at least it has a kind of symmetry under rescaling! You can see this from the formula
by noting that both the Laplacian and have units of length-2. So, they both transform in the same way under rescaling: if you take any smooth function
, apply
and then expand the result by a factor of
you get
times what you get if you do those operations in the other order.
In particular, this means that if you have a smooth eigenfunction of with eigenvalue
you will also have one with eigenfunction
for any
And if your original eigenfunction was normalizable, so will be the new one!
With some calculation you can show that when the Hamiltonian
has a smooth normalizable eigenfunction with a negative eigenvalue. In fact it’s spherically symmetric, so finding it is not so terribly hard. But this instantly implies that
has smooth normalizable eigenfunctions with any negative eigenvalue.
This implies various things, some terrifying. First of all, it means that is not bounded below, at least not on the space of smooth normalizable functions. A similar but more delicate scaling argument shows that it’s also not bounded below on
as I claimed earlier.
This is scary but not terrifying: it simply means that when the potential is too strongly negative for the Hamiltonian to be bounded below.
The terrifying part is this: we’re getting uncountably many normalizable eigenfunctions, all with different eigenvalues, one for each choice of A self-adjoint operator on a countable-dimensional Hilbert space like
can’t have uncountably many normalizable eigenvectors with different eigenvalues, since then they’d all be orthogonal to each other, and that’s too many orthogonal vectors to fit in a Hilbert space of countable dimension!
This sounds like a paradox, but it’s not. These functions are not all orthogonal, and they’re not all eigenfunctions of a self-adjoint operator. You see, the operator is not self-adjoint on the domain we’ve chosen, the space of all smooth functions in
We can carefully choose a domain to get a self-adjoint operator… but it turns out there are many ways to do it.
Intriguingly, in most cases this choice breaks the naive dilation symmetry. So, we’re getting what physicists call an ‘anomaly’: a symmetry of a classical system that fails to give a symmetry of the corresponding quantum system.
Of course, if you’ve made it this far, you probably want to understand what the different choices of Hamiltonian for a particle in an inverse cube force law actually mean, physically. The idea seems to be that they say how the particle changes phase when it hits the singularity at and bounces back out.
(Why does it bounce back out? Well, if it didn’t, time evolution would not be unitary, so it would not be described by a self-adjoint Hamiltonian! We could try to describe the physics of a quantum particle that does not come back out when it hits the singularity, and I believe people have tried, but this requires a different set of mathematical tools.)
For a detailed analysis of this, it seems one should take Schrödinger’s equation and do a separation of variables into the angular part and the radial part:
For each choice of one gets a space of spherical harmonics that one can use for the angular part
The interesting part is the radial part,
Here it is helpful to make a change of variables
At least naively, Schrödinger’s equation for the particle in the potential then becomes
where
Beware: I keep calling all sorts of different but related Hamiltonians and this one is for the radial part of the dynamics of a quantum particle in an inverse cube force. As we’ve seen before in the classical case, the centrifugal force and the inverse cube force join forces in an ‘effective potential’
where
So, we have reduced the problem to that of a particle on the open half-line moving in the potential
The Hamiltonian for this problem:
is called the Calogero Hamiltonian. Needless to say, it has fascinating and somewhat scary properties, since to make it into a bona fide self-adjoint operator, we must make some choice about what happens when the particle hits The formula above does not really specify the Hamiltonian.
This is more or less where Gitman, Tyutin and Voronov begin their analysis, after a long and pleasant review of the problem. They describe all the possible choices of self-adjoint operator that are allowed. The answer depends on the values of but very crudely, the choice says something like how the phase of your particle changes when it bounces off the singularity. Most choices break the dilation invariance of the problem. But intriguingly, some choices retain invariance under a discrete subgroup of dilations!
So, the rabbit hole of the inverse cube force law goes quite deep, and I expect I haven’t quite gotten to the bottom yet. The problem may seem pathological, verging on pointless. But the math is fascinating, and it’s a great testing-ground for ideas in quantum mechanics—very manageable compared to deeper subjects like quantum field theory, which are riddled with their own pathologies. Finally, the connection between the inverse cube force law and centrifugal force makes me think it’s not a mere curiosity.
In four dimensions
It’s a bit odd to study the inverse cube force law in 3-dimensonal space, since Newtonian gravity and the electrostatic force would actually obey an inverse cube law in 4-dimensional space. For the classical 2-body problem it doesn’t matter much whether you’re in 3d or 4d space, since the motion stays on the plane. But for quantum 2-body problem it makes more of a difference!
Just for the record, let me say how the quantum 2-body problem works in 4 dimensions. As before, we can work in the center of mass frame and consider this Hamiltonian:
And as before, the behavior of this Hamiltonian depends on Here’s the story this time:
• In this case
is essentially self-adjoint on
So, it admits a unique self-adjoint extension and there’s no ambiguity about this case.
• In this case
is not essentially self-adjoint on
• In this case the expected energy
is bounded below for
So, there is exists a canonical ‘best choice’ of self-adjoint extension, called the Friedrichs extension.
• In this case the expected energy is not bounded below, so we don’t have the Friedrichs extension to help us choose which self-adjoint extension is ‘best’.
I’ve been assured these are correct by Barry Simon, and a lot of this material will appear in Section 7.4 of his book:
• Barry Simon, A Comprehensive Course in Analysis, Part 4: Operator Theory, American Mathematical Society, Providence, RI, 2015.
See also:
• Barry Simon, Essential self-adjointness of Schrödinger operators with singular potentials, Arch. Rational Mech. Analysis 52 (1973), 44–48.
Notes
The animation was made by ‘WillowW’ and placed on Wikicommons. It’s one of a number that appears in this Wikipedia article:
• Newton’s theorem of revolving orbits, Wikipedia.
I made the graphs using the free online Desmos graphing calculator.
The picture of a spiral was made by ‘Anarkman’ and ‘Pbroks13’ and placed on Wikicommons; it appears in
• Hyperbolic spiral, Wikipedia.
The hyperbolic spiral is one of three kinds of orbits that are possible in an inverse cube force law. They are vaguely analogous to ellipses, hyperbolas and parabolas, but there are actually no bound orbits except perfect circles. The three kinds are called Cotes’s spirals. In polar coordinates, they are:
• the epispiral:
• the hyperbolic spiral:
• the Poinsot spiral:



Inverse cube if we lived in 4 spatial dims
Hi, Jim—great to hear from you!
Now you’ve got me wondering about something. Gravity and the electrostatic field would naturally obey an inverse cube force law if we lived in 4 spatial dimensions. But how would the self-adjointness of the Hamiltonian
work in this dimension? Annoying, Reed and Simon have a nice discussion of this operator in 5 spatial dimensions in Example 4 of Chapter X.2 of their book Methods of Modern Mathematical Physics II: Fourier Analysis and Self-Adjointness. They also give theorems that handle this operator in more than 5 dimensions. But I don’t see how it works in 4 dimensions.
In 3 dimensions, I explained that this Hamiltonian has different behavior depending on whether ,
, 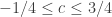 , or
, or 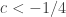 .
.
In 5 dimensions, Reed and Simon show it has very different behavior depending on whether
• Then it’s essentially self-adjoint on
Then it’s essentially self-adjoint on 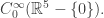
• Then it’s not essentially self-adjoint on this domain, but it’s bounded below, so we can use the Friedrichs extension.
Then it’s not essentially self-adjoint on this domain, but it’s bounded below, so we can use the Friedrichs extension.
• Then it’s not essentially self-adjoint on this domain and not bounded below.
Then it’s not essentially self-adjoint on this domain and not bounded below.
I find it truly amazing that we see such delicate behavior in both 3 and 5 dimensions. Usually if something like this just barely works in some dimension, it either works completely or not at all in higher dimensions.
But I want to know what’s going on in 4 dimensions!
Ah, I figured out what some of what happens in dimensions! The Hardy inequality in
dimensions! The Hardy inequality in  dimensions says the Hamiltonian
dimensions says the Hamiltonian
is bounded below for
For this gives
this gives 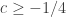 , for
, for  this gives
this gives  and for
and for 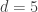 this gives
this gives 
It should be possible to show the operator is not bounded below for
but I haven’t shown that.
Okay, here’s some more progress! On MathSciNet I read that this paper:
• Barry Simon, Essential self-adjointness of Schrödinger operators with singular potentials, Arch. Rational Mech. Analysis 52 (1973), 44–48.
proves:
Here I believe we must have though people often use the opposite sign convention,
though people often use the opposite sign convention,  to make it a nonnegative operator. This matters here, but I’m going to assume I’m right.
to make it a nonnegative operator. This matters here, but I’m going to assume I’m right.
Anyway, the function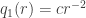 is in
is in  , and we can take
, and we can take 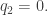 So, the key condition is that
So, the key condition is that
and when we have
we have
so this theorem only says that is essentially self-adjoint on
is essentially self-adjoint on 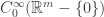 when
when
That’s not useless… but it’s useless for attractive potentials.
Let me just see how this theorem fares in 3 and 5 dimensions, where I already know stuff.
When we have
we have
so this theorem says that is essentially self-adjoint on
is essentially self-adjoint on 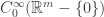 when
when
Good, this matches what’s in my blog article!
When we have
we have
so this theorem says that is essentially self-adjoint on
is essentially self-adjoint on 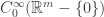 when
when
Good! This matches what I said in an earlier comment!
Small correction in the section about changing potentials into
potentials into  ones:
ones:
“But you’ll notice this trick doesn’t actually work at , the case that corresponds to the inverse cube force law.”
, the case that corresponds to the inverse cube force law.”
I believe you mean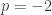 .
.
Whoops! Thanks, I’ll fix that.
I enjoyed this post particularly much. I’m not trained enough in mathematical physics to absorb all details in managable time. But I still understood pleasantly much. I really like how you catch the eye here with an interesting piece of classical mechanics and then move over to quantum mechanics. Also, it fascinates me how such a seemingly simple investigation can lead into such deep waters. In particular, the issue of (possibly ambiguous) completability to a self-adjoint operator is intriguing. (And a bit scary.)
I’m glad you liked it Carsten! I’ve been sort of missing you over at G+, wondering how your studies of physics are going. The inverse cube law illustrates a lot of interesting issues in physics, even though it’s an esoteric topic.
The issue of multiple different self-adjoint extensions is easier to understand when you have a free particle on the interval![[0,1],](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D%2C&bg=ffffff&fg=333333&s=0&c=20201002) with the usual Hamiltonian
with the usual Hamiltonian
or just
if you want to keep the calculations clean. This operation is not symmetric on the space of all smooth functions on![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) , since
, since
for such functions. If you restrict to smooth functions that vanish at the endpoints, you get
(these are fun calculations to do), but the operator on this domain has infinitely many self-adjoint extensions! Each one of these extensions describes different physics. Each one gives a different recipe for what happens when the particle hits the ends of the interval! It can ‘wrap around’ and come back in at the other end, it can ‘bounce off’, but it can also do either of these things while acquiring an arbitrary phase, and it can also do a superposition of these two things.
In this case you can work out everything very clearly and it becomes intuitive.
For a particle in an attractive inverse cube force, or an even stronger force, the issue is what happens when the particle hits the central singularity. I still haven’t understood in concrete terms what are all the options! What happens can depend on its angular momentum, and for each choice of angular momentum the paper by Gitman, Tyutin and Voronov lists the possibilities. But I’d like a more ‘synthetic’ view, that provides more physical intuition. It’s possible that this is still an open problem.
I’m also curious about work that lets the particle ‘fall down the hole and never come back’. This yields nonunitary time evolution. In his thesis, Gopalkrishnan writes:
Since Hille was the thesis advisor of my thesis advisor Irving Segal, and Nelson had Segal as his thesis advisor, I feel some family obligation to learn what Nelson did here.
[I’ve been trying to comment since yesterday, but G+ authentication here has stopped working for me despite trying different browsers. So I’m using Twitter authentication now.]
Hi John, thanks for your elaborate reply! I’ll boldly display my ignorance and ask: what exactly is meant by “extension” of a self-adjoint operator? Let’s consider the simple Hamiltonian from your reply. Does “extension” mean extending its domain to smooth functions on an interval larger as the unit interval, while still requiring that the functions vanish at 0 and 1?
As for my studies of physics – it’s actually quite comical: I was trying to inch my way towards QFT, and an acquaintance recommended my the book “PCT, Spin and Statistics, and All That” by Streater and Wightman. I started reading an realized I wasn’t quite ready for it. In particular, I wanted to learn more about operator theory and distributions first. While ploughing through operators, I realized that I didn’t even understand why the Riemann integral won’t do for Hilbert spaces. So I looked closely at the Lebesgue integral. That lead me into measure theory. Then I found Terry Tao’s book “An introduction to measure theory”. And I couldn’t bring myself to just skim it. So I’m currently working my way through that. (Tao, bless him, has the nice habit of turning proofs of essential insights into exercises…)
Fortunately, my deadlines are in software engineering, and not in physics or maths :)
Carsten wrote:
Actually I was talking about taking an operator that’s not self-adjoint and trying to extend it to make it self-adjoint. So your real question is: what’s an extension of an operator?
And the answer is: an operator is a kind of function, and I think you know what it means to extend a function. But there’s more to say.
Yes, if you’d stopped there your answer would be correct. The linear operators that physicists like are rarely operators that map all of a Hilbert space
that map all of a Hilbert space  to itself. They’re usually defined on just part of the Hilbert space. So, they are linear operators
to itself. They’re usually defined on just part of the Hilbert space. So, they are linear operators 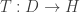 where
where  is a linear subspace called the domain of
is a linear subspace called the domain of  To extend
To extend  means to find a new operator
means to find a new operator  where
where 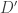 is a bigger domain, such that
is a bigger domain, such that 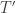 equals
equals  on the original domain:
on the original domain:
Anyway…
That’s almost never how it works. A more typical example would be this. We start with
defined on the domain consisting of all smooth functions on the unit interval that vanish at the endpoints. This operator is symmetric:
consisting of all smooth functions on the unit interval that vanish at the endpoints. This operator is symmetric:
but it’s not self-adjoint. So, we might try to extend this operator to get something self-adjoint. For example, we could take an operator
which looks just like except it has a bigger domain
except it has a bigger domain 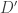 : all functions
: all functions  with second derivative in
with second derivative in 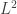 obeying ‘periodic boundary conditions’:
obeying ‘periodic boundary conditions’:
This operator is self-adjoint! Since I haven’t defined ‘self-adjoint’ that’s not so easy to check, but it’s easy to check that it’s still symmetric:
As you can see, this stuff is a bit technical. But it’s important, because the ‘same-looking’ operator can actually be different self-adjoint operators, describing different physics, depending on the domain! For example, if I changed only this equation in what I said above:
we’d have a new domain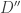 and a new self-adjoint operator
and a new self-adjoint operator
with this new domain… and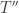 has quite different properties than
has quite different properties than  It describes particle that pick up a phase of -1 when they hit one end of the unit interval and pop out the other end!
It describes particle that pick up a phase of -1 when they hit one end of the unit interval and pop out the other end!
Both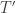 and
and 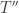 are self-adjoint extensions of
are self-adjoint extensions of 
Yikes, that’s a hard way to start learning QFT—your acquaintance must have been a sadist. This book assumes you know quantum field theory and are eager to make it mathematically rigorous. At the very least all the stuff I explained just now about operators should be familiar to you before try to climb that mountain. But I see you backed down.
Okay, good! If you’re still interested in analysis after that, I’d suggest Reed and Simon’s Methods of Modern Mathematical Physics I: Functional Analysis. This leads you rapidly but (I think) clearly through analysis from topology and measure theory, through distributions, up to self-adjoint operators on Hilbert space, all the while paying a lot of attention to their applications in physics. I really loved it when I was learning this stuff.
Thanks! The notion of extension of an operator is clear to me now, and also that a typical case involves relaxing boundary conditions of the functions on which it operates. I also understand now that changing the domain can change the set of “candidate adjoints”, ideally to a singleton set containing only the operator itself. (Did I get this right?)
I’m really glad about the advice on Wightman/Streater and Reed/Simon. It had dawned on me that my next step should be studying a certain bunch of maths, which miraculously agrees with what Reed/Simon seems to cover. So after finishing Tao’s book I’ll just pick up Reed/Simon.
Carsten wrote:
All that is exactly right! So, I’ll reward (or punish) you with a bit more information.
Often it is difficult or annoying to describe the domain of a self-adjoint operator. So, we often settle for an essentially self-adjoint operator: one that has a unique self-adjoint extension.
Any self-adjoint operator is essentially self-adjoint, with its unique self-adjoint extension being itself. But essential self-adjointness is a very useful generalization.
For example, here is an essentially self-adjoint operator:
with the domain consisting of all smooth functions
consisting of all smooth functions  on the unit interval obeying
on the unit interval obeying
The unique self-adjoint extension of is the operator
is the operator
with the larger domain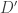 consisting of all functions
consisting of all functions  with
with
and with second derivative lying in![L^2[0,1]](https://s0.wp.com/latex.php?latex=L%5E2%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) .
.
As you can see, saying “second derivative lying in![L^2[0,1]](https://s0.wp.com/latex.php?latex=L%5E2%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) ” sounds more technical than saying “smooth” (infinitely differentiable). We need to be technical because we’re trying to describe the “exactly correct” domain instead of something that’s “almost right”, but a bit smaller. And in more complicated examples, the exactly correct domain is almost impossible to describe explicitly.
” sounds more technical than saying “smooth” (infinitely differentiable). We need to be technical because we’re trying to describe the “exactly correct” domain instead of something that’s “almost right”, but a bit smaller. And in more complicated examples, the exactly correct domain is almost impossible to describe explicitly.
Anyway, it’s all explained very nicely near the end of Reed and Simon. Good luck on that, and don’t hesitate to ask questions, especially in public forums where I can have the pleasure of showing off in my reply! I like analysis and hardly ever get to talk about it these days.
Okay, I’ll file your reply under “reward” rather than “punishment” ;) So, sticking with your example, does some spectral theorem yield an orthogonal Eigenbasis for the self-adjoint operator that’s the unique extension? If so, that would be intriguing: we might only be interested in the smooth functions, but we’d have to “step out” of that domain for an Eigenbasis… (Feel free to say “Shut up now and read the book” :)
Self-adjoint operators on infinite-dimensional Hilbert spaces typically don’t have a basis of eigenvectors: the simplest example is the operator of multiplication by on the Hilbert space
on the Hilbert space  The would-be eigenvectors are Dirac deltas, which are not in
The would-be eigenvectors are Dirac deltas, which are not in  and there’s a continuum of them—too many for an orthonormal basis of
and there’s a continuum of them—too many for an orthonormal basis of 
The spectral theorem in its grown-up, infinite-dimensional form tells you how to deal with this. Needless to say, physicists pretend the infinite-dimensional case is just like the finite-dimensional case… but Reed and Simon give a rigorous treatment of this crucial issue.
Thanks again! My immediate curiosity is sated now :) Time for the book.
Another fascinating post! Another thought provoking demonstration! I’m wondering if another solution might obtain out of Richard Anthony Proctor’s book: ‘A Treatise on the Cycloid and all Forms of Cycloid Curves’ (1787) See: https://archive.org/details/atreatiseoncycl01procgoog
Do you know some relation between cycloids and the inverse cube force law?
I should start by remembering the closed-form solutions of the inverse cube force laws. There’s information about that here:
• Binet equation: Cotes spirals, Wikipedia.
Here are the equations of the epispiral:
the hyperbolic spiral:
and the Poinsot spiral:
All this looks like really beautiful, classical mathematics—a modified version of the theory of ellipses, hyperbolas and parabolas. The equation of the epispiral reminds me slightly of the cycloid.
Since gravity and the electrostatic force would naturally obey an inverse cube force law if space were 4-dimensional, I decided to do some reading and figure out how the Hamiltonian
acts in 4 dimensions. I checked my answers with Barry Simon, the champ of mathematical physics.
And I was happy to discover that my answers were all correct! Moreover, a lot of this material will appear in his forthcoming book A Comprehensive Course in Analysis, Part 4: Operator Theory.
So, here’s the story:
• In this case
In this case  is essentially self-adjoint on
is essentially self-adjoint on  So, it admits a unique self-adjoint extension and there’s no ambiguity about this case.
So, it admits a unique self-adjoint extension and there’s no ambiguity about this case.
• In this case
In this case  is not essentially self-adjoint on
is not essentially self-adjoint on 
• In this case the expected energy
In this case the expected energy  is bounded below for
is bounded below for 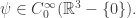 It thus has a canonical ‘best choice’ of self-adjoint extension, the Friedrichs extension.
It thus has a canonical ‘best choice’ of self-adjoint extension, the Friedrichs extension.
• In this case the expected energy is not bounded below, so we don’t have the Friedrichs extension to help us choose which self-adjoint extension is ‘best’.
In this case the expected energy is not bounded below, so we don’t have the Friedrichs extension to help us choose which self-adjoint extension is ‘best’.
In short, it’s the same as in 3 dimensions, but with the numbers 0 and -1 replacing 3/4 and -1/4. The situation is ‘better’ than in 3 dimensions.
The E-field equations for dipole radiation include inverse cube terms.
http://en.wikipedia.org/wiki/Dipole_antenna#Hertzian_dipole
I am thinking (I don’t know if it is true) that if there is an infinitesimal transformation of the potential (that depends on a single parameter) then the space-temporal coordinates could have a coordinate transformation with a single parameter that could change the trajectory in the original trajectory, so that could be possible to use the Noether theorem (that must be true for each little parameters variation) to obtain a invariant of the transformation (close trajectories are close trajectories for a cubic potential, so that the transformation could be simple in this case).
If the infinitesimal transformation of the potential is little, then the trajectory variation is little, and it could be possible an (infinitesimal) coordinates trasformation to obtain an invariant of the trajectory: it could be possible to obtain an invariant that connect coordinates variations with potential variation (like in the case of field theory) for a classical system.
I’m not sure how closely this is related, but it’s an interesting question nonetheless:
Take a rubber strip (i.e. a cut rubber band, reducing the genus from 1 to 0) fixed at both ends, or a guitar string, or whatever. Take hold of it somewhere and pull it. What results are two lines connecting the end points with the pulled-away point.
Do the same with a two-dimensional analog, e.g. a trampoline. In this case, the result is not a cone, but rather a curved surface, with the slope greater the closer one is to the “disturbance”. (Side question: in an ideal case, is the slope infinite when the disturbance is a point?) Is there an obvious reason for this? What, exactly, is the form of this curved surface? Is there a general formula, say for a three-dimensional “surface” embedded in a four-dimensional space?
It’s fairly related. I believe it’s a pretty reasonable approximation to say your -dimensional surface (e.g. rubber band for
-dimensional surface (e.g. rubber band for  or trampoline for
or trampoline for  ) is trying to minimize its volume (e.g. length for
) is trying to minimize its volume (e.g. length for  or area for
or area for  ), subject to the boundary conditions you’re giving it, including the ‘disturbance’ at a chosen point.
), subject to the boundary conditions you’re giving it, including the ‘disturbance’ at a chosen point.
At the very least, this makes for a fun and much-studied math problem! The case is called the theory of minimal surfaces. There are big textbooks on this, and also on the general framework that works in higher dimensions: geometric measure theory.
case is called the theory of minimal surfaces. There are big textbooks on this, and also on the general framework that works in higher dimensions: geometric measure theory.
Geometric measure theory is famous for being difficult. I just noticed that on Amazon, Frank Morgan’s Geometric Measure Theory: A Beginner’s Guide has just one review, a two-star review that says (among other things):
On the other hand, Federer’s Geometric Measure Theory has some better reviews, but also a one-star review that reads:
Another review suggests getting both Morgan’s book and Federer’s book, and reading them side by side. And that’s probably good advice!
Anyway, when your minimal surface isn’t ‘too warped’, you can approximately describe its height as a function
obeying the Laplace equation. Then the things I’m saying about singularities in the gravitational field, or electrostatic field, become rather closely related to your observations. I think the big difference is that the gravitational field of a point particle obey the equation
(so, Poisson’s equation with a delta function ‘source’) while the problem you mention is about
except at the origin, where
and the points on the sphere of radius 1, where
on the sphere of radius 1, where
(so, the Laplace equation with some Dirichlet boundary conditions).
Thanks for the reply. What would I do without you? :-)
What happens if the boundary conditions move to infinity? Can an infinite area be minimized?
If even you say that geometric measure theory is difficult, I wonder if I have time to master it in the rest of my life. What is the form of the surfaces for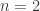 ,
,  , and
, and  ?
?
Phillip wrote:
We face this problem whenever we try to apply the principle of least action to a field on an infinite-sized chunk of spacetime. The way people deal with it is to replace ‘minimization’ by a principle saying that if you change your field within some finite-sized region, the quantity you’re trying to minimize doesn’t change, to first order:
where is our field,
is our field,  is the quantity we wish to minimize (like action or area), and
is the quantity we wish to minimize (like action or area), and 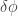 is a change in the field—and we demand
is a change in the field—and we demand  outside some set of finite volume!
outside some set of finite volume!
This makes everything well-defined, usually, and we can derive some differential equation that should satisfy. For area-minimizing surfaces this equation was first found by Lagrange himself.
should satisfy. For area-minimizing surfaces this equation was first found by Lagrange himself.
I don’t think you want to. But you might like to look at a gallery of minimal surfaces. These are typically only area-minimizing in the subtle sense I just described.
I should know some of those, but I don’t!
“I should know some of those, but I don’t!”
Definitely a challenge to the readers here!
No takers? Really?
I came across an interesting paper which does real mathematical physics on a stretched 2-dimensional rubber sheet (like those sometimes used to demonstrate gravity and/or which are confused with embedding diagrams). Some interesting tidbits:
“there does not exist a two-dimensional, cylindrically-symmetric surface that will yield rolling marble orbits that are equivalent to the particle orbits of Newtonian gravitation,[3] or for particle orbits that arise in general relativity”
“they found a Kepler-like expression of the form T3 / r2, which is reminiscent of Kepler’s third law for planetary orbits, but with the powers transposed”
“a differential equation that determines the shape of the fabric warped by the mass …nonlinear, ordinary differential equation that cannot be solved analytically” [my emphasis]
https://xkcd.com/895/
Next time we’ll look at what happens to point particles interacting electromagnetically when we take special relativity into account. After that, we’ll try to put special relativity and quantum mechanics together!
For more on the inverse cube force law, see:
• John Baez, The inverse cube force law, Azimuth, 30 August 2015.
To understand what a great triumph this is, one needs to see what could have gone wrong! Suppose space had an extra dimension. In 3-dimensional space, Newtonian gravity obeys an inverse square force law because the area of a sphere is proportional to its radius squared. In 4-dimensional space, the force obeys an inverse cube law. Using a cube instead of a square makes the force stronger at short distances, with dramatic effects. For example, even for the classical 2-body problem, the equations of motion no longer ‘almost always’ have a well-defined solution for all times. For an open set of initial conditions, the particles spiral into each other in a finite amount of time!
The quantum version of this theory is also problematic. The uncertainty principle is not enough to save the day. The inequalities above no longer hold: kinetic energy does not triumph over potential energy. The Hamiltonian is no longer essentially self-adjoint on the set of wavefunctions that I described.
[…] An article by Baez on the inverse cube force law. […]