This summer my students Brendan Fong and Blake Pollard visited me at the Centre for Quantum Technologies, and we figured out how to understand open continuous-time Markov chains! I think this is a nice step towards understanding the math of living systems.
Admittedly, it’s just a small first step. But I’m excited by this step, since Blake and I have been trying to get this stuff to work for a couple years, and it finally fell into place. And we think we know what to do next.
Here’s our paper:
• John C. Baez, Brendan Fong and Blake S. Pollard, A compositional framework for open Markov processes.
And here’s the basic idea…
Open detailed balanced Markov processes
A continuous-time Markov chain is a way to specify the dynamics of a population which is spread across some finite set of states. Population can flow between the states. The larger the population of a state, the more rapidly population flows out of the state. Because of this property, under certain conditions the populations of the states tend toward an equilibrium where at any state the inflow of population is balanced by its outflow.
In applications to statistical mechanics, we are often interested in equilibria such that for any two states connected by an edge, say 
I’m getting tired of saying ‘continuous-time Markov chain’, so from now on I’ll just say ‘Markov process’, just because it’s shorter. Okay? That will let me say the next sentence without running out of breath:
Our paper is about open detailed balanced Markov processes.
Here’s an example:
The detailed balanced Markov process itself consists of a finite set of states together with a finite set of edges between them, with each state 
These populations and rate constants are required to obey an equation called the ‘detailed balance condition’. This equation means that in equilibrium, the flow from
To get an ‘open’ detailed balanced Markov process, some states are designated as inputs or outputs. In general each state may be specified as both an input and an output, or as inputs and outputs multiple times. See how that’s happening in this example? It may seem weird, but it makes things work better.
People usually say Markov processes are all about how probabilities flow from one state to another. But we work with un-normalized probabilities, which we call ‘populations’, rather than probabilities that must sum to 1. The reason is that in an open Markov process, probability is not conserved: it can flow in or out at the inputs and outputs. We allow it to flow both in and out at both the input states and the output states.
Our most fundamental result is that there’s a category 
We compose morphisms in 
with the previously shown morphism 
And here’s our second most fundamental result: the category 
The so-called compactness is also important. This means we can take some inputs of an open Markov process and turn them into outputs, or vice versa. For example, using the compactness of
In fact all the categories in our paper are dagger compact categories, and all our functors preserve this structure. Dagger compact categories are a well-known framework for describing systems with inputs and outputs, so this is good.
The analogy to electrical circuits
In a detailed balanced Markov process, population can flow along edges. In the detailed balanced equilibrium, without any flow of population from outside, the flow along from state
In an electrical circuit made of linear resistors, charge can flow along wires. In equilibrium, without any driving voltage from outside, the current along each wire will be zero. The potentials will be equal at every node.
This sets up an analogy between detailed balanced continuous-time Markov chains and electrical circuits made of linear resistors! I love analogy charts, so this makes me very happy:
| Circuits | Detailed balanced Markov processes |
| potential | population |
| current | flow |
| conductance | rate constant |
| power | dissipation |
This analogy is already well known. Schnakenberg used it in his book Thermodynamic Network Analysis of Biological Systems. So, our main goal is to formalize and exploit it. This analogy extends from systems in equilibrium to the more interesting case of nonequilibrium steady states, which are the main topic of our paper.
Earlier, Brendan and I introduced a way to ‘black box’ a circuit and define the relation it determines between potential-current pairs at the input and output terminals. This relation describes the circuit’s external behavior as seen by an observer who can only perform measurements at the terminals.
An important fact is that black boxing is ‘compositional’: if one builds a circuit from smaller pieces, the external behavior of the whole circuit can be determined from the external behaviors of the pieces. For category theorists, this means that black boxing is a functor!
Our new paper with Blake develops a similar ‘black box functor’ for detailed balanced Markov processes, and relates it to the earlier one for circuits.
When you black box a detailed balanced Markov process, you get the relation between population–flow pairs at the terminals. (By the ‘flow at a terminal’, we more precisely mean the net population outflow.) This relation holds not only in equilibrium, but also in any nonequilibrium steady state. Thus, black boxing an open detailed balanced Markov process gives its steady state dynamics as seen by an observer who can only measure populations and flows at the terminals.
The principle of minimum dissipation
At least since the work of Prigogine, it’s been widely accepted that a large class of systems minimize entropy production in a nonequilibrium steady state. But people still fight about the the precise boundary of this class of systems, and even the meaning of this ‘principle of minimum entropy production’.
For detailed balanced open Markov processes, we show that a quantity we call the ‘dissipation’ is minimized in any steady state. This is a quadratic function of the populations and flows, analogous to the power dissipation of a circuit made of resistors. We make no claim that this quadratic function actually deserves to be called ‘entropy production’. Indeed, Schnakenberg has convincingly argued that they are only approximately equal.
But still, the ‘dissipation’ function is very natural and useful—and Prigogine’s so-called ‘entropy production’ is also a quadratic function.
Black boxing
I’ve already mentioned the category 
A morphism in the category 
A morphism in the category 
In our previous paper, Brendan and I introduced these two categories and a functor between them, the ‘black box functor’:
The idea is that any circuit determines a linear relation between the potentials and net current flows at the inputs and outputs. This relation describes the behavior of a circuit of resistors as seen from outside.
Our new paper introduces a black box functor for detailed balanced Markov processes:
We draw this functor as a white box merely to distinguish it from the other black box functor. The functor 
How do we manage to black box detailed balanced Markov processes? We do it using the analogy with circuits!
The analogy becomes a functor
Every analogy wants to be a functor. So, we make the analogy between detailed balanced Markov processes and circuits precise by turning it into a functor:
This functor converts any open detailed balanced Markov process into an open electrical circuit made of resistors. This circuit is carefully chosen to reflect the steady-state behavior of the Markov process. Its underlying graph is the same as that of the Markov process. So, the ‘states’ of the Markov process are the same as the ‘nodes’ of the circuit.
Both the equilibrium populations at states of the Markov process and the rate constants labelling edges of the Markov process are used to compute the conductances of edges of this circuit. In the simple case where the Markov process has exactly one edge from any state
where:
• 
• 
• 
The detailed balance condition for Markov processes says precisely that the matrix
A triangle of functors
If you paid careful attention, you’ll have noticed that I’ve described a triangle of functors:
And if you know anything about how category theorists think, you’ll be wondering if this diagram commutes.
In fact, this triangle of functors does not commute! However, a general lesson of category theory is that we should only expect diagrams of functors to commute up to natural isomorphism, and this is what happens here:
The natural transformation 
The functors 
in fact an isomorphism of vector spaces, which converts potential-current pairs into population-flow pairs in a manner that depends on the
But here’s the key point. The naturality of 
is any morphism in 
Since 
This equation has a clear intuitive meaning! It says that to compute the behavior of a detailed balanced Markov process, namely 
What we really do
So that’s a sketch of what we do, and I hope you ask questions if it’s not clear. But I also hope you read our paper! Here’s what we actually do in there. After an introduction and summary of results:
• Section 3 defines open Markov processes and the open master equation.
• Section 4 introduces detailed balance for open Markov
processes.
• Section 5 recalls the principle of minimum power
for open circuits made of linear resistors, and explains how to black box them.
• Section 6 introduces the principle of minimum dissipation for open detailed balanced Markov processes, and describes how to black box these.
• Section 7 states the analogy between circuits and detailed balanced Markov processes in a formal way.
• Section 8 describes how to compose open Markov processes, making them into the morphisms of a category.
• Section 9 does the same for detailed balanced Markov processes.
• Section 10 describes the ‘black box functor’ that sends any open detailed balanced Markov process to the linear relation describing its external behavior, and recalls the similar functor for circuits.
• Section 11 makes the analogy between between open detailed balanced Markov processes and open circuits even more formal, by making it into a functor. We prove that together with the two black box functors, this forms a triangle that commutes up to natural isomorphism.
• Section 12 is about geometric aspects of this theory. We show that the linear relations in the image of these black box functors are Lagrangian relations between symplectic vector spaces. We also show that the master equation can be seen as a gradient flow equation.
• Section 13 is a summary of what we have learned.
Finally, Appendix A is a quick tutorial on decorated cospans. This is a key mathematical tool in our work, developed by Brendan in an earlier paper.
Azimuth 
Got some broken images there…
I don’t see any problems.
Well, it’s fixed now. Not sure what happened.
Sorry to be thick, but I don’t get it. In the first Markov process, apart from the fact that you used the plural, “outputs”, when pointing to the circle with a 2 in it at the right of the diagram, how are we meant to know that this “was specified as an output twice”? And similarly, how do we know that the circle with a 2 in it at the left of the second Markov process counts as two inputs?
I also have no idea what the specific implications would be of a state being an n-fold input or output. If a population is initially flowing into a state in process A that is nominated as a 3-fold output, how does that population flow within the composite Markov process BA in which it somehow has to be spread between 3 different states that were 3 different input states of process B? Or can a 3-fold output only be joined to a 3-fold input, rather than 3 separate 1-fold inputs?
Greg wrote:
Whoops! In fact, these pictures don’t illustrate that subtle issue.
This business about states being multiple inputs or outputs is one of those nitpicky technical details that turns out to make the machine run more smoothly, but seems only weird and confusing at first.
I’ll eventually answer your questions about that, and you’ll see it’s all very nice. But right now I’m being called to dinner!
Okay, let me answer this:
For starters, let me discuss the case of Markov processes rather than detailed balanced Markov processes, which are slightly more complicated.
For us a Markov process consists of a finite set
of nodes or states, a finite set 
of edges or transitions, maps
assigning each edge its source and target, and a map
assigning a rate constant to each edge. So, we’ve got a graph (a ‘directed multigraph’, to be painfully precise) where nodes are states, edges are transitions between states, and each transition has a rate constant.
To make our Markov process into an open Markov process we simply equip it with two maps
where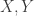
are arbitrary finite sets. Elements of 
are inputs, and the input map 
says how to interpret these inputs as states. Elements of 
are outputs, and the output map 
says how to interpret these outputs as states. This is the stuff that was not drawn clearly in the pictures in this blog article (which I may fix).
Note that we don’t require
and 
to be one-to-one. Nor do we require them to have disjoint ranges. So, a state in 
can correspond to more than one input, or more than one output, or both. I need to convince you that this is a good thing.
For this, I need to say a word about how we compose open Markov processes.
Note that an open Markov process consists in part of maps
In this situation we want to think of our open Markov process as a ‘morphism’ from
to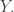 
That means want to be able to compose it with an open Markov process that’s a morphism from 
to some finite set 
, like this:
We do this by ‘gluing the outputs of the first open Markov process to the inputs of the second’. That is, we identify each state of the form
for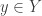 
with the corresponding state 
I hope you can visualize how this will let us build a new graph by gluing together the two we started with—and indeed a new open Markov process! This will be a morphism from 
to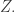 
Now I’m ready to explain why it’s good to let states correspond to more than one input, or more than one output, or both.
A category needs to have identity morphisms. What will an identity morphism be like? It will be a graph with no edges, and thus no need for rate constants. It will have some set
of nodes, each of which is in the image of both the input and output maps! The input and output maps will be identity functions, like this:
I hope you see that composing this with some other open Markov process gives that same open Markov process back. That’s good: composing with an identity morphism should have no effect.
Well, this has been rather long, and I still haven’t explained why it’s good to let the input and output maps fail to be one-to-one. Briefly: we can use composition with these to turn inputs of an open Markov process into outputs, or vice versa. This is the ‘compactness’ stuff mentioned in the blog article.
By now I should have implicitly answered your question, but let’s see:
In my example
what you’re calling a ‘3-fold output’ is a point in
that’s in the image of 3 different points of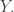 
That is, we have 
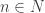with
for exactly three distinct points
When we compose this open Markov process with another, we identify
with all 3 points 
(Typo at top: s,t should have values in N, not X)
Beautiful! It induced in me severe mathematical hallucinations. They only stopped at functors from nCob to Hilb: Is Life a topological stochastico-quantum field theory?
Thanks, Flori – I fixed that typo.
I’m glad you like this stuff. Indeed, I’m taking concepts from topological quantum field theory and adapting them. But instead of chopping spacetime into pieces, I’m chopping ‘space’—or some abstraction thereof, like an electrical circuit—and chopping it into pieces. And instead of doing a quantum theory, and getting linear operators between Hilbert spaces of quantum states, I’m doing a classical theory, and getting linear Lagrangian relations between symplectic vector spaces describing classical boundary conditions. This seems like a good way to go…
So far we’re mainly doing statics, or almost statics, like ‘nonequilibrium steady states’, or problems where you use the Laplace transform to convert an ODE into a mere algebra problem. But with some 2-categories we can do true dynamics.
It turns out I was completely wrong when I wrote:
In fact the pictures in this blog article don’t illustrate that subtle possibility…. which is fine. So, I’ve deleted this parenthetical remark from my blog article!
Thanks for explaining this! And sorry to make you write such a long reply. I ended up looking at the paper as well … and if anyone else reading this is as confused as I was, page 23 of the paper makes it much clearer what happens when you compose Markov processes where some states are n-fold outputs.
Don’t be sorry! I’ve been working hard on this paper for the last 2 months, and now I’m eager to talk about it.
Would you mind saying a bit more about how Markov processes can help explain the math of living systems?
I’ve been working to understand the Markov process/Wiener process/integral (unsure of the distinctions here, clarification welcome) in Laurent Nottale’s work, as a method of transitioning back and forth between quantum and classical realms. I’m also curious to hear more about the Markov process’ relationship to imaginary time and brown noise in the context of understanding the math of living systems…
Lots in there, so feel free to just pick one that might jump out at you. I majored in Physics as an undergrad, but beyond that am largely self-taught in physics and math. I did my gradute work in philosophy of physics and tend to approach from the conceptual/philosophical side before adding the mathematical elaboration, if that helps to frame your response.
Love your blog – thanks!
Kerri wrote:
Since Blake and I are planning to write some papers on this subject, I’ll beg you to wait for those. I’ll definitely blog about them, and I’m really eager to talk about this line of work, but I don’t think it’s a good idea to explain it before I actually do it!
For now I recommend this:
• J. Schnakenberg, Thermodynamic Network Analysis of Biological Systems, Springer, Berlin, 1981.
This paper is more recent and more advanced, but it has lots of references and it’s free:
• Matteo Polettini and Massimiliano Esposito, Irreversible thermodynamics of open chemical networks I: Emergent cycles and broken conservation laws.
Excellent. Thank you!
If I understood correctly then at any time instant one could normalize the “populations” and thus compute things like entropy, relative entropy and information (with respect to the equilibrium population) at any instant. Since open Markov processes are used in thermodynamics I suspect a lot has been studied in that context? Like does e.g. relative information also decrease in an understandable fashion like here, if inputs and outputs are fixed?
Yes, in open Markov processes relative information decreases if the input and output populations are fixed. I forgot to remind everyone that Blake has a paper about this stuff. He blogged about it here:
• Blake Pollard, A Second Law for open Markov processes, Azimuth, 15 November 2014.
Schnakenberg has also written about related things.
I didn’t look at Blakes paper but I looked at the blog post. I feel a bit uncomfortable with the fact that you don’t normalize, I wrote about that in a comment to that blog post. So in some sense I interpreted this as “your approach”, but there may be others, who normalize. I currently have no intuition wether normalizing is important or not I just want to get a better picture of whats going on there. Like for the formula for the relative information I think the normalization was used.
It’s incredibly important for us to not normalize. Our work is all about putting together little Markov processes to form big ones, but you can alternatively think of it as being about taking a big one and breaking it into smaller pieces. If you have some set of states on which the probability distribution is normalized, and you break it into smaller pieces, it will not be normalized on each of these smaller pieces.
Another way to put it is this: if you want to study open systems where probability flows in or out, you can’t demand that the probability distribution sum to 1 at all times. (One of my missions is to generalize everything to open systems.)
For closed systems, conservation laws say some quantity doesn’t change. For open systems, conservation laws merely state that the change in this quantity can be completely accounted for by some kind of flow through the boundary… and that when you glue together two systems to form a larger one, the flow from system A to system B is minus the flow from system B to system A.
Luckily, most of the key properties of Markov processes, entropy etc. easily generalize to the non-normalized case. Blake has been busy doing this, starting with the paper I just mentioned.
I understand that for the composition it may be important not to normalize, but for computing entropies, especially with respect to a comparision to closed systems I could imagine that it makes sense to normalize. At least one could compare non normalized and normlaized approaches. Finally -at least in my understanding- entropy is loosely speaking quite about proportions. I dont have the time to check what it means to give up normalization with respect to the axiomatic approach to entropy. Here for example people seem to generalize discrete probability distributions to socalled Choquet capacities and at least in this article it seems they prefer to normalize for deriving a generalized entropy (I found the paper only “au hasard” and just browsed through it):
But as far as I can tell they don’t say why they restrict themselves.
[…] Let’s see what we get if we ‘black-box’ glycolysis. I’ve written about black-boxing electrical circuits and Markov processes: it’s a way to ignore their inner workings and focus on the relation between inputs and outputs […]
Blake Pollard considers a concrete class of open systems, a very large class called ‘open Markov processes’. He shows that nonequilibrium steady states obey the principle of minimum entropy production only approximately—with the approximation being good for steady states that are near equilibrium!
However, he shows that another minimum principle holds exactly, even for steady states that are far from equilibrium. He calls this the ‘principle of minimum dissipation’.
We actually discussed the principle of minimum dissipation in an earlier paper:
• John Baez, Brendan Fong and Blake Pollard, A compositional framework for Markov processes. (Blog article here.)
But one advantage of Blake’s new paper is that it presents the results with a minimum of category theory. Of course I love category theory, and I think it’s the right way to formalize open systems, but it can be intimidating.
Lately we’ve been thinking about open Markov processes. These are random processes where something can hop randomly from one state to another (that’s the ‘Markov process’ part) but also enter or leave the system (that’s the ‘open’ part).
The ultimate goal is to understand the nonequilibrium thermodynamics of open systems—systems where energy and maybe matter flows in and out. If we could understand this well enough, we could understand in detail how life works. That’s a difficult job! But one has to start somewhere, and this is one place to start.
We have a few papers on this subject:
• Blake Pollard, A Second Law for open Markov processes. (Blog article here.)
• John Baez, Brendan Fong and Blake Pollard, A compositional framework for Markov processes. (Blog article here.)
• Blake Pollard, Open Markov processes: A compositional perspective on non-equilibrium steady states in biology. (Blog article here.)
Blake Pollard is a student of mine in the physics department here at U. C. Riverside. Together with Brendan and me, he developed a category-theoretic approach to Markov processes: random processes where a system hops around between different states. We used Brendan’s general formalism to reduce Markov processes to electrical circuits. Now Blake is going further and using these ideas to tackle chemical reaction networks.
Blake Pollard is a student of mine in the physics department here at U. C. Riverside. Together with Brendan and me, he developed a category-theoretic approach to Markov processes: random processes where a system hops around between different states. We used Brendan’s general formalism to reduce Markov processes to electrical circuits. Now Blake is going further and using these ideas to tackle chemical reaction networks.
At some point I gave Brendan Fong a project: describe the category whose morphisms are electrical circuits. He took up the challenge much more ambitiously than I’d ever expected, developing powerful general frameworks to solve not only this problem but also many others. He did this in a number of papers, most of which I’ve already discussed […]
Kenny Courser and I have been working hard on this paper for months:
• John Baez and Kenny Courser, Coarse-graining open Markov processes.
A while back, Brendan Fong, Blake Pollard and I showed that these constructions make open Markov processes into the morphisms of a symmetric monoidal category:
• A compositional framework for Markov processes, Azimuth, January 12, 2016.
Here Kenny and I go further by constructing a symmetric monoidal double category where the 2-morphisms include ways of coarse-graining open Markov processes. We also extend the previously defined ‘black-boxing’ functor from the category of open Markov processes to this double category.
Two students in the Applied Category Theory 2018 school wrote a blog article about Brendan Fong’s theory of decorated cospans:
• Jonathan Lorand and Fabrizio Genovese, Hypergraph categories of cospans, The n-Category Café, 28 February 2018.
What’s especially interesting to me is that both Jonathan and Fabrizio know some mathematical physics, and they’re part of a group who will be working with me on some problems as part of the Applied Category Theory 2018 school! Brendan and Blake Pollard and I used symplectic geometry and decorated cospans to study the black-boxing of electrical circuits and Markov processes… maybe we should try to go further with that project!
I’m giving a talk on some work I did with Kenny Courser. It’s part of the ACT2020 conference, and it’s happening on 20:40 UTC on Tuesday July 7th, 2020. (That’s 1:40 pm here in California, just so I don’t forget.)
Like all talks at this conference, you can watch it live on Zoom or on YouTube. It’ll also be recorded, so you can watch it later on YouTube too, somewhere here.
You can see my slides now, and read some other helpful things:
• Coarse-graining open Markov processes.