I’m visiting the University of Genoa and talking to two category theorists: Marco Grandis and Giuseppe Rosolini. Grandis works on algebraic topology and higher categories, while Rosolini works on the categorical semantics of programming languages.
Yesterday, Marco Grandis showed me a fascinating paper by his thesis advisor:
• Gabriele Darbo, Aspetti algebrico-categoriali della teoria dei dispotivi, Symposia Mathematica IV (1970), Istituto Nazionale di Alta Matematica, 303–336.
It’s closely connected to Brendan Fong’s thesis, but also different—and, of course, much older. According to Grandis, Darbo was the first person to work on category theory in Italy. He’s better known for other things, like ‘Darbo’s fixed point theorem’, but this piece of work is elegant, and, it seems to me, strangely ahead of its time.
The paper’s title translates as ‘Algebraic-categorical aspects of the theory of devices’, and its main concept is that of a ‘universe of devices’: a collection of devices of some kind that can be hooked up using wires to form more devices of this kind. Nowadays we might study this concept using operads—but operads didn’t exist in 1970, and Darbo did quite fine without them.
The key is the category which has finite sets as objects and ‘corelations’ as morphisms. I explained corelations here:
• Corelations in network theory, 2 February 2016.
Briefly, a corelation from a finite set to a finite set
is a partition of the disjoint union of
and
We can get such a partition from a bunch of wires connecting points of
and
The idea is that two points lie in the same part of the partition iff they’re connected, directly or indirectly, by a path of wires. So, if we have some wires like this:

they determine a corelation like this:

There’s an obvious way to compose corelations, giving a category
Gabriele Darbo doesn’t call them ‘corelations’: he calls them ‘trasduttori’. A literal translation might be ‘transducers’. But he’s definitely talking about corelations, and like Fong he thinks they are basic for studying ways to connect systems.
Darbo wants a ‘universe of devices’ to assign to each finite set a set
of devices having
as their set of ‘terminals’. Given a device in
and a corelation
thought of as a bunch of wires, he wants to be able to attach these wires to the terminals in
and get a new device with
as its set of terminals. Thus he wants a map
If you draw some pictures, you’ll see this should give a functor
Moreover, if we have device with a set of terminals and a device with a set
of terminals, we should be able to set them side by side and get a device whose set of terminals form the set
, meaning the disjoint union of
and
So, Darbo wants to have maps
If you draw some more pictures you can convince yourself that should be a lax symmetric monoidal functor… if you’re one of the lucky few who knows what that means. If you’re not, you can look it up in many places, such as Section 1.2 here:
• Brendan Fong, The Algebra of Open and Interconnected Systems, Ph.D. thesis, University of Oxford, 2016. (Blog article here.)
Darbo does not mention lax symmetric monoidal functors, perhaps because such concepts were first introduced by Mac Lane only in 1968. But as far as I can tell, Darbo’s definition is almost equivalent to this:
Definition. A universe of devices is a lax symmetric monoidal functor
One difference is that Darbo wants there to be exactly one device with no terminals. Thus, he assumes is a one-element set, say
, while the definition above would only demand the existence of a map
obeying a couple of axioms. That gives a particular ‘favorite’ device with no terminals. I believe we get Darbo’s definition from the above one if we further assume
is the identity map. This makes sense if we take the attitude that ‘a device is determined by its observable behavior’, but not otherwise. This attitude is called ‘black-boxing’.
Darbo does various things in his paper, but the most exciting to me is his example connected to linear electrical circuits. He defines, for any pair of objects and
in an abelian category
a particular universe of devices. He calls this the universe of linear devices having
as the object of potentials and
as the object of currents.
If you don’t like abelian categories, think of as the category of finite-dimensional real vector spaces, and let
Electric potential and electric current are described by real numbers so this makes sense.
The basic idea will be familiar to Fong fans. In an electrical circuit made of purely conductive wires, when two wires merge into one we add the currents to get the current on the wire going out. When one wire splits into two we duplicate the potential to get the potentials on the wires going out. Working this out further, any corelation between finite set determines two linear relations, one
relating the currents on the wires coming in to the currents on the wires going out, and one
relating the potentials on the wires going out to the potentials on the wires coming in. Here is the direct sum of
copies of
and so on; the funky arrow indicates that we have a linear relation rather than a linear map. Note that
goes forward while
goes backward; this is mainly just conventional, since you can turn linear relations around, but we’ll see it’s sort of nice.
If we let be the set of linear relations between two objects
we can use the above technology to get a universe of devices where
In other words, a device of this kind is simply a linear relation between the potentials and currents at its terminals!
How does get to be a functor
? That’s pretty easy. We’ve defined it on objects (that is, finite sets) by the above formula. So, suppose we have a morphism (that is, a corelation)
How do we define
To answer this question, we need a function
Luckily, we’ve got linear relations
and
So, given any linear relation we just define
Voilà!
People who have read Fong’s thesis, or my paper with Blake Pollard on reaction networks:
• John Baez and Blake Pollard, A compositional framework for reaction networks.
will find many of Darbo’s ideas eerily similar. In particular, the formula
appears in Lemma 16 of my paper with Blake, where we are defining a category of open dynamical systems. We prove that is a lax symmetric monoidal functor, which is just what Darbo proved—though in a different context, since our
is not linear like his, and for a different purpose, since he’s trying to show
is a ‘universe of devices’, while we’re trying to construct the category of open dynamical systems as a ‘decorated cospan category’.
In short: if this work of Darbo had become more widely known, the development of network theory could have been sped up by three decades! But there was less interest in a general theory of networks at the time, lax monoidal functors were brand new, operads unknown… and, sadly, few mathematicians read Italian.
Darbo has other papers, and so do his students. We should read them and learn from them! Here are a few open-access ones:
• Franco Parodi, Costruzione di un universo di dispositivi non lineari su una coppia di gruppi abeliani, Rendiconti del Seminario Matematico della Università di Padova 58 (1977), 45–54.
• Franco Parodi, Categoria degli universi di dispositivi e categoria delle T-algebre, Rendiconti del Seminario Matematico della Università di Padova 62 (1980), 1–15.
• Stefano Testa, Su un universo di dispositivi monotoni, Rendiconti del Seminario Matematico della Università di Padova 65 (1981), 53–57.
At some point I will scan in G. Darbo’s paper and make it available here.

This is all far beyond my mathematical knowledge, but it did remind me of something silly I’ll risk sharing. It relates to devices in the everyday sense.
Davis’s law of small devices:
A device can be made arbitrarily small if it doesn’t have to work.
If I’m not mistaken, is also known as the partition category. The corresponding algebra (a splendid survey is by Halverson and Ram, https://arxiv.org/abs/math/0401314), where you only consider morphisms between sets of a fixed size
is also known as the partition category. The corresponding algebra (a splendid survey is by Halverson and Ram, https://arxiv.org/abs/math/0401314), where you only consider morphisms between sets of a fixed size  , is the centralizer algebra
, is the centralizer algebra  of the symmetric group,
of the symmetric group,  being its defining representation, when
being its defining representation, when  is at least
is at least 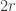 .
.
More precisely, when you compose two morphisms, some blocks may lose contact to the input and the output. In this case, these blocks (let’s say there are of them) are omitted and the result is multiplied with the
of them) are omitted and the result is multiplied with the  -th power of a parameter, usually denoted
-th power of a parameter, usually denoted  .
.
When is small, there is a basis of the centralizer algebra indexed (!) by set partitions into at most
is small, there is a basis of the centralizer algebra indexed (!) by set partitions into at most  blocks.
blocks.
Still, there are some mysterious open questions…
Hey, that’s cool! I hadn’t thought of linearizing this category! This is connected to Blake Stacey’s comment on taking formal linear combinations of morphisms in a category to get a new ‘linear’ category. It’s nice how the representation theory of the symmetric group shows up here. This could be pretty important, at least in applications of network theory to linear systems.
By the way, to use TeX here, you have to enclose the math with
$latex $
with the word ‘latex’ appearing directly after the first dollar sign, no space between, but then a space after it.
Indeed, the idea of Blake Stacey is what Bruce and I try to expand upon in https://arxiv.org/abs/1408.3592 – warning: this paper is still work in progress…
(thank you for fixing my syntax!)
Nice! I hadn’t known, or had forgotten, that you are collaborating with Bruce Westbury. I really like his paper on a diagrammatic approach to normed division algebras (or more precisely, composition algebras).
Nice paper, Martin Rubey, thanks!
Thank you! Just very recently, Georgia Benkart and Tom Halverson got a step further: https://arxiv.org/abs/1707.01410
I am still trying to figure out a refinement, I hope I’ll manage!