
In the fourth talk of the ACT@UCR seminar, Michael Shulman told us how to create nice string diagams for any closed symmetric monoidal category.
Mike had to teach right after his talk, but he rejoined us for discussions later at the Category Theory Community Server, here:
You can view or join the conversation there if you sign in.
You can see his slides here, or download a video of his talk here, or watch the video here:
• April 22, Michael Shulman, Star-autonomous envelopes.
Abstract. Symmetric monoidal categories with duals, a.k.a. compact monoidal categories, have a pleasing string diagram calculus. In particular, any compact monoidal category is closed with [A,B] = (A* ⊗ B), and the transpose of A ⊗ B → C to A → [B,C] is represented by simply bending a string. Unfortunately, a closed symmetric monoidal category cannot even be embedded fully-faithfully into a compact one unless it is traced; and while string diagram calculi for closed monoidal categories have been proposed, they are more complicated, e.g. with “clasps” and “bubbles”. In this talk we obtain a string diagram calculus for closed symmetric monoidal categories that looks almost like the compact case, by fully embedding any such category in a star-autonomous one (via a functor that preserves the closed structure) and using the known string diagram calculus for star-autonomous categories. No knowledge of star-autonomous categories will be assumed.
His talk is based on this paper:
• Michael Shulman, Star-autonomous envelopes.
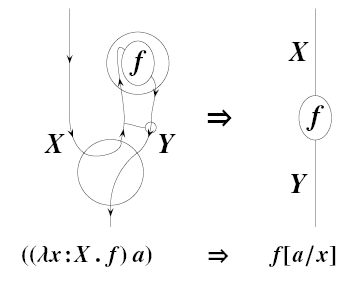
This subject is especially interesting to me since Mike Stay and I introduced string diagrams for closed monoidal categories in a somewhat ad hoc way in our Rosetta Stone paper—but the resulting diagrams required clasps and bubbles:
This is the string diagram for beta reduction in the cartesian closed category coming from the lambda calculus.

Will a recording of this be available? Seems relevant to linguistics (for glue semantics=semantic composition by linear logic for ling. structures that aren’t trees), but don’t fancy my chances of effecting a Zoom capture at 3AM (Eastern Aus Time)
Yes, you can see it on YouTube now—look at the blog article again. I should have said that. Every lecture in the ACT@UCR seminar series will show up on YouTube later that same day.
A key issue is how to express the bijection fundamental to the lifting property (used to express Kan extensions 2-categorically) using string diagrams.
An interesting discussion of this issue, well-motivated by the lambda-calculus, is at:
“Kan Extensions for Program Optimization, Or: Art and Dan Explain An Old Trick” by Ralf Hinze
Click to access Kan.pdf