
As an undergrad I learned a lot about partial derivatives in physics classes. But they told us rules as needed, without proving them. This rule completely freaked me out. If derivatives are kinda like fractions, shouldn’t this equal 1?
Let me show you why it’s -1.
First, consider an example:

This example shows that the identity is not crazy. But in fact it
holds the key to the general proof! Since is a coordinate system we can assume without loss of generality that
. At any point we can approximate
to first order as
for some constants
. But for derivatives the constant
doesn’t matter, so we can assume it’s zero.
Then just compute!

There’s also a proof using differential forms that you might like
better. You can see it here, along with an application to
thermodynamics:
But this still leaves us yearning for more intuition — and for me, at least, a more symmetrical, conceptual proof. Over on Twitter, someone named
Postdoc/cake provided some intuition using the same example from thermodynamics:
Using physics intuition to get the minus sign:
- increasing temperature at const volume = more pressure (gas pushes out more)
- increasing temperature at const pressure = increasing volume (ditto)
- increasing pressure at const temperature = decreasing volume (you push in more)
Jules Jacobs gave the symmetrical, conceptual proof that I was dreaming of:
This proof is more sophisticated than my simple argument, but it’s very pretty, and it generalizes to higher dimensions in ways that’d be hard to guess otherwise.
He uses some tricks that deserve explanation. As I’d hoped, the minus signs come from the anticommutativity of the wedge product of 1-forms, e.g.
But what lets us divide quantities like this? Remember, are all functions on the plane, so
are 1-forms on the plane. And since the space of 2-forms at a point in the plane is 1-dimensional, we can divide them! After all, given two vectors in a 1d vector space, the first is always some number times the second, as long as the second is nonzero. So we can define their ratio to be that number.
For Jacobs’ argument, we also need that these ratios obey rules like
But this is easy to check: whenever are vectors in a 1-dimensional vector space, division obeys the above rule. To put it in fancy language, nonzero vectors in any 1-dimensional real vector space form a ‘torsor’ for the multiplicative group of nonzero real numbers:
• John Baez, Torsors made easy.
Finally, Jules used this sort of fact:
Actually he forgot to write down this particular equation at the top of his short proof—but he wrote down three others of the same form, and they all work the same way. Why are they true?
I claim this equation is true at some point of the plane whenever are smooth functions on the plane and
doesn’t vanish at that point. Let’s see why!
First of all, by the inverse function theorem, if at some point in the plane, the functions
and
serve as coordinates in some neighborhood of that point. In this case we can work out
in terms of these coordinates, and we get
or more precisely
Thus
so
as desired!



I encourage my Calculus students not to fear thinking of derivatives as ratios, but partial derivatives mess this up. You can still think of them as ratios using the trick with higher-order exterior forms that Jules Jacobs used, but that's a little heavy for the beginning of the multivariable course. So instead I emphasize the subscript indicating what is to be held fixed (even though it's nowhere to be found in the textbook). can even be broken into
can even be broken into  and you can move those partial differentials around freely in an algebraic expression, but you can't cancel
and you can move those partial differentials around freely in an algebraic expression, but you can't cancel  .
.
Neat!
John, you were an undergrad at Princeton.
Who taught your Advanced Calculus, or whatever the multi-variable calculus course was called, and what textbook did they use?
(Nickerson, Spencer, and Steenrod?)
Another popular text back then was Tom Apostol, Mathematical Analysis: A Modern [for 1957!] Approach to Advanced Calculus.
Anyhow, thanks very much for your illuminating discussion of this situation!
I took that course at George Washington University when I was a senior in high school, and apparently the textbook was unmemorable. In practice, I got good at this stuff from taking physics courses, and reading Feynman’s Lectures on Physics.
Well, that’s certainly interesting. Thanks for explaining that. I had wondered why you so often discussed learning math from physics texts.
BTW, texts at one time popular for some approximation to that course were:
1957 Apostol, Mathematical Analysis
1959 Nickerson, Spencer, and Steenrod, Advanced Calculus (Princeton Math 303-304)
1965 Fleming, Functions of Several Variables
(1965 Spivak, Calculus on Manifolds (very concise notes))
1968 Loomis & Sternberg, Advanced Calculus (Harvard Math 55)
1968 Lang, Analysis I, 1983, 1997 Undergraduate Analysis
Just thought I’d mention those texts in case anyone cares to opine on them.
(I wonder what text Toby uses.)
Re Feynman, let me put in a plug for a most excellent, and free!!, on-line version of his lectures:
https://www.feynmanlectures.caltech.edu/.
Like John, I also took multivariable calculus at my local university while I was in high school. I don't remember who the author of the textbook was, but I don't think that it was substantially different from the textbooks in common use at state universities in the USA today. I really learnt the subject the next year, reading Spivak's Calculus on Manifolds in the university's library. (First I read his regular calculus textbook, then Calculus on Manifolds, then his 5-volume magnum opus on differential geometry, although I didn't finish the last or understand all of what I did read of it.)
As for what I use, I teach this course at my local community college, from an ordinary textbook that we get from our contracted publisher, along with course notes that I've written that look a bit more under the hood. You can find the latter at http://tobybartels.name/MATH-2080/2021FA/ (or start at http://tobybartels.name/MATH-2080/ for a more up-to-date version if you're reading this in 2022 or later).
There is a not-so-well-known book by Michael Spivak that is worth mentioning:
Physics for Mathematicians: Mechanics I.
Concerning that book, Spivak’s friend, mentor, and colleague Richard S. Palais wrote:
After extensive and thorough coverage of hidden assumptions in the subject, Spivak moves forward to a treatment of Lagrangian and Hamiltonian mechanics, relying on his books on DG.
Here is another proof using forms; no intuition, just algebra.
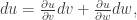


 in the right-hand side. Taking into account
in the right-hand side. Taking into account  and
and 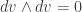 , we find
, we find
 But
But  and
and 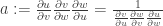 , so we get
, so we get 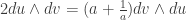 , whence
, whence  .
.
Wedge the first two equations with each other and use the third to replace
Thanks. Neither my proof nor Jules Jacobs’ nor the argument in the video used ‘intuition’, though my quick proof sketch didn’t fill in the details of every step, e.g. justifying that you can work to first order at a point.
I too yearn for an intuitive proof and I regret that I don’t have one, as I tried to indicate in my comment.
Oh, sorry—for some silly reason I thought you were using “intuition” in the derogatory sense, like “lack of rigor”. Of course one wants a rigorous proof that also provides a good intuition for why the result is true!
The functional dependence among ,
,  and
and  defines a surface. The normal direction to the surface is given by the gradients
defines a surface. The normal direction to the surface is given by the gradients  or
or  . Since these must be parallel we have
. Since these must be parallel we have  and
and  . The first is satisfied trivially, while the second, upon multiplication by
. The first is satisfied trivially, while the second, upon multiplication by 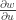 yields the required the identity. The geometric intuition is that however we look at the surface the normal direction is the same.
yields the required the identity. The geometric intuition is that however we look at the surface the normal direction is the same.
The way I learned (and taught) it, based on having some identity relation , was just to use implicit differentiation – ie using the chain rule on the LHS of
, was just to use implicit differentiation – ie using the chain rule on the LHS of  to get
to get 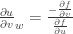 . The “intuition” is then just that implicit differentiation always introduces a minus sign compared to what you’d get by simply “cancelling differentials”.
. The “intuition” is then just that implicit differentiation always introduces a minus sign compared to what you’d get by simply “cancelling differentials”.
On the question of derivatives acting like fractions, you should see the paper “Total and Partial Differentials as Algebraically Manipulable Entities”.
https://arxiv.org/abs/2210.07958