42

In The Hitchhiker’s Guide to the Galaxy by Douglas Adams, the number 42 is the “Answer to the Ultimate Question of Life, the Universe, and Everything”. But he didn’t say what the question was!

Since today is Towel Day, let me reveal that now.

If you try to get several regular polygons to meet snugly at a point in the plane, what’s the most sides any of the polygons can have? The answer is 42.

The picture shows an equilateral triangle, a regular heptagon and a regular 42-gon meeting snugly at a point. If you do the math, you’ll see the reason this works is that

\displaystyle{ \frac{1}{3} + \frac{1}{7} + \frac{1}{42} = \frac{1}{2} }

There are actually 10 solutions of

\displaystyle{ \frac{1}{p} + \frac{1}{q} + \frac{1}{r} = \frac{1}{2} }

with p \le q \le r, and each of them gives a way for three regular polygons to snugly meet at a point. But this particular solution features the biggest number possible!

But why is this so important? Well, it turns out that if you look for natural numbers a, b, c that make

\displaystyle{ \frac{1}{a} + \frac{1}{b} + \frac{1}{c} }

as close to 1 as possible, while still less than 1, the very best you can do is 1/2 + 1/3 + 1/7. It comes within 1/42 of equalling 1, since

\displaystyle{ \frac{1}{3} + \frac{1}{7} + \frac{1}{42} = \frac{1}{2} }

And why is this important? Well, suppose you’re trying to make a doughnut with at least two holes that has the maximum number of symmetries. More precisely, suppose you’re trying to make a Riemann surface with genus g \ge 2 that has the maximum number of symmetries. Then you need to find a highly symmetrical tiling of the hyperbolic plane by triangles whose interior angles are \pi/a, \pi/b and \pi/c , and you need

\displaystyle{ \frac{1}{a} + \frac{1}{b} + \frac{1}{c} < 1 }

for these triangles to fit on the hyperbolic plane.

For example, if you take a = 2, b = 3, c = 7 you get this tiling:

A clever trick then lets you curl up the hyperbolic plane and get a Riemann surface with at most

\displaystyle{ \frac{2(g-1)}{1 - \frac{1}{a} - \frac{1}{b} - \frac{1}{c}} }

symmetries.

So, to get as many symmetries as possible, you want to make 1 - \frac{1}{a} - \frac{1}{b} - \frac{1}{c} as small as possible! And thanks to what I said, the best you can do is

\displaystyle{ 1 - \frac{1}{2} - \frac{1}{3} - \frac{1}{7} = \frac{1}{42} }

So, your surface can have at most

84(g-1)

symmetries. This is called Hurwitz’s automorphism theorem. The number 84 looks mysterious when you first see it — but it’s there because it’s twice 42.

In particular, the famous mathematician Felix Klein studied the most symmetrical doughnut with 3 holes. It’s a really amazing thing, called Klein’s quartic curve:

It has

84 \times 2 = 168

symmetries. That number also looks mysterious when you first see it. Of course it’s the number of hours in a week, but the real reason it’s there is because it’s four times 42.

If you carefully count the triangles in the picture above, you’ll get 56. However, these triangles are equilateral, or at least they would be if we could embed Klein’s quartic curve in 3d space without distorting it. If we drew all the smaller triangles whose interior angles are \pi/2, \pi/3 and \pi/7, each equilateral triangle would get subdivided into 6 smaller triangles, and there would be a total of 6 \times 56 = 336 triangles. But of course

336 = 8 \times 42

Half of these smaller triangles would be ‘left-handed’ and half would be ‘right-handed’, and there’d be a symmetry sending a chosen triangle to any other triangle of the same handedness, for a total of

168 = 4 \times 42

symmetries (that is, conformal transformations, not counting reflections).

But why is this stuff the answer to the ultimate question of life, the universe, and everything? I’m not sure, but I have a crazy theory. Maybe all matter and forces are made of tiny little strings! As they move around, they trace out Riemann surfaces in spacetime. And when these surfaces are as symmetrical as possible, reaching the limit set by Hurwitz’s automorphism theorem, the size of their symmetry group is a multiple of 42, thanks to the math I just described.

Puzzles

Puzzle 1. Consider solutions of

\displaystyle{ \frac{1}{p} + \frac{1}{q} + \frac{1}{r} = \frac{1}{2} }

with positive integers p \le q \le r, and show that the largest possible value of r is 42.

Puzzle 2. Consider solutions of

\displaystyle{ \frac{1}{a} + \frac{1}{b} + \frac{1}{c} < 1}

with positive integers a, b, c, and show that the largest possible value of \frac{1}{a} + \frac{1}{b} + \frac{1}{c} is 1 - \frac{1}{42}.

Acknowledgments and references

For more details, see my page on Klein’s quartic curve, and especially the section on incredibly symmetrical surfaces. Sums of reciprocals of natural numbers are called ‘Egyptian fractions’, and they have deep connections to geometry; for more on this see my article on Archimedean tilings and Egyptian fractions.

The picture of a triangle, heptagon and 42-gon (also known as a tetracontakaidigon) was made by Tyler, and you can see all 17 ways to get 3 regular polygons to meet snugly at a vertex on Wikipedia. Of these, only 11 can occur in a uniform tiling of the plane. The triangle, heptagon and 42-gon do not tile the plane, but you can see some charming attempts to do something with them on Kevin Jardine’s website Imperfect Congruence:


The picture of Klein’s quartic curve was made by Greg Egan, and you should also check out his page on Klein’s quartic curve.


“Good Morning,” said Deep Thought at last.
“Er…good morning, O Deep Thought” said Loonquawl nervously, “do you have…er, that is…”
“An Answer for you?” interrupted Deep Thought majestically. “Yes, I have.”
The two men shivered with expectancy. Their waiting had not been in vain.
“There really is one?” breathed Phouchg.
“There really is one,” confirmed Deep Thought.
“To Everything? To the great Question of Life, the Universe and everything?”
“Yes.”
Both of the men had been trained for this moment, their lives had been a preparation for it, they had been selected at birth as those who would witness the answer, but even so they found themselves gasping and squirming like excited children.
“And you’re ready to give it to us?” urged Loonsuawl.
“I am.”
“Now?”
“Now,” said Deep Thought.
They both licked their dry lips.
“Though I don’t think,” added Deep Thought. “that you’re going to like it.”
“Doesn’t matter!” said Phouchg. “We must know it! Now!”
“Now?” inquired Deep Thought.
“Yes! Now…”
“All right,” said the computer, and settled into silence again. The two men fidgeted. The tension was unbearable.
“You’re really not going to like it,” observed Deep Thought.
“Tell us!”
“All right,” said Deep Thought. “The Answer to the Great Question…”
“Yes…!”
“Of Life, the Universe and Everything…” said Deep Thought.
“Yes…!”
“Is…” said Deep Thought, and paused.
“Yes…!”
“Is…”
“Yes…!!!…?”
“Forty-two,” said Deep Thought, with infinite majesty and calm. – Douglas Adams

This entry was posted on Saturday, May 25th, 2013 at 3:44 pm and is filed under mathematics. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.

51 Responses to 42

  1. Jon Awbrey says:
    25 May, 2013 at 4:00 pm

    Not to mention Jackie Robinson …

    Reply
  2. John Baez says:
    25 May, 2013 at 8:57 pm

    One interesting thing is that it’s not true for every g ≥ 2 that we can find a complex structure on the g-holed torus, making it into a Riemann surface, that has a symmetry group of size 84(g-1). My first draft of this post was a bit misleading about this, because I was confused.

    We can find one for the 3-holed torus, but apparently not for the 2-holed torus—what’s the best we can do in that case?

    As I mentioned, the 3-holed torus has a complex structure whose symmetry group is PSL(2,7), with 168 = 84 × 2 elements. This is Klein’s quartic curve, discovered in 1878.

    The next case that works is apparently the 7-holed torus, which can be given a complex structure whose symmetry group PSL(2,8), with 504 = 84 × 6 elements. This is the Fricke–Macbeath curve, discovered by Fricke in 1899.

    Then comes the 14-holed torus, which can be given three different complex structures with 1092 = 84 × 13 symmetries. These are called the first Hurwitz triplet. Somehow they arise from the fact that in the ring of algebraic integers in some field, the prime 13 splits as a product of three distinct prime ideals.

    So, it’s a complicated and interesting subject.

    Reply
    • westy31 says:
      29 May, 2013 at 9:48 pm

      A picture of a genus 2 object with 12 heptagons:

      Glue together the tetrahedral ends to close the surface. Although each heptagon is identically situated in the figure, the 7 sides of a heptagon do not see identical landscapes. So its not Platonic, nevertheless interesting.

      Gerard

      Reply
    • Zeno Rogue (@ZenoRogue) says:
      23 November, 2018 at 3:22 pm

      It appears that counting symmetries is not the only reasonable way to determine the winner in the “most symmetric surface” contest. The most symmetric shape on the plane is the circle, as shown by the biggest ratio of the radius (i.e. a line from the center to the boundary) to the area. All surfaces of the given genus have the same area, so we could argue that the winner is the surface with the largest systole (which is a bit similar to the radius).

      For genus 3, we have the Klein Quartic based on {7,3} which wins in symmetry counting, but we also have Schmutz’s M(3) which is based on {12,3}. If you are inside the surface, what you see is the covering hyperbolic plane: in the Klein quartic you see 14 (closest) copies of yourself arranged symmetrically around you, in M(3) you see only 12 of them, but the layout in M(3) is more symmetric: in KQ the distance is 4.080620 if you are standing in the center of the heptagon and 3.935946 if you are standing optimally (and that number is the systole); in M(3) the distance is 4.317779 in the center of dodecagon and 3.983305 optimally.

      For genus 2 we have Bolza’s Surface which is based on {8,3} and also has the greatest systole, for genus 4 we have Bring’s surface based on {5,4} with 58(4-1) automorphisms and Schmutz’s M(4) based on {12,3} with 122(4-1) automorphisms. M(4) again wins in terms of systole.

      Wikipedia lists the maximum number of isometries for each genus from 2 to 4: https://en.wikipedia.org/wiki/Riemann_surface#Isometries_of_Riemann_surfaces I have learned about M(3) and M(4) from pages on Klein’s Quartic and Bring’s Curve pages respectively.

      I have just implemented MacBeath’s Surface, Bring’s Surface, M(3), M(4), so I know what they look like :) I already had Klein Quartic and a surface which turned out to be one of the first Hurwitz triplet (one with the smallest systole, unfortunately).

      (By look like, I mean the universal cover with orbits marked… I think this is much more informative than a “donut with g holes” display)

      Reply
  3. Bruce McNeill says:
    25 May, 2013 at 10:26 pm

    I thought the Q was 7×6

    Reply
    • Graham Jones says:
      26 May, 2013 at 9:29 am

      I remember 7×8.

      Reply
      • G. says:
        27 May, 2013 at 8:11 am

        No, its “What do you get if you multiply six by nine?” :)

        Reply
      • John Baez says:
        28 May, 2013 at 12:56 am

        If you’re interested in 7 × 8, read this article of mine. It’s about a 7-dimensional shape with 56 corners, sometimes (though rarely) called the hecatonicosihexapentacosiheptacontihexaexon.

        For some reason ever since my wife left for a trip to England I’ve been in the mood for the goofy sort of math I used to work on.

        Reply
    • Bruce Smith says:
      27 May, 2013 at 4:24 pm

      Somewhere in the 4th or 5th book it’s hinted (ambiguously) that the Q was “pick a number, any number”.

      Reply
  4. meditationatae says:
    25 May, 2013 at 10:29 pm

    I noticed in the hyperbolic tiling by heptagons (on the page at math.ucr.edu) that one gets from a heptagon numbered k to another one numbered k through four heptagon “hops”: from one heptagon to an adjacent one on to another, and so on. It also appears that from a heptagon numbered k, one can always get to a second heptagon numbered k in four “hops”. Is it a general rule that for the periodic hyperbolic tilings like the one for the Klein quartic, that folding them up can be associated with some complex projective curve (Riemann surface)? What values are possible for the genus g, i.e. number of holes? Great post …

    Reply
    • John Baez says:
      25 May, 2013 at 11:03 pm

      meditationate wrote:

      Is it a general rule that for the periodic hyperbolic tilings like the one for the Klein quartic, that folding them up can be associated with some complex projective curve (Riemann surface)?

      Yes. There are some general phenomena going on here, and people know a huge amount about them, but I’m having a bit of trouble saying exactly what they all are.

      First, any solution of

      \displaystyle{ \frac{1}{a} + \frac{1}{b} + \frac{1}{c} <1}

      gives a highly symmetrical tiling of hyperbolic space by triangles. The symmetry group of this tiling is discrete subgroup of the symmetry group of the hyperbolic plane, called a hyperbolic Coxeter group. It’s really worthwhile looking at some examples, because they’re beautiful:

      • Hyperbolic tiling, Wikipedia.

      I showed you the (2,3,7) tiling, coming from

      \displaystyle{ \frac{1}{2} + \frac{1}{3} + \frac{1}{7} = \frac{41}{42} < 1 }

      but the (2,4,5) tiling is also nice:

      It comes from

      \displaystyle{ \frac{1}{2} + \frac{1}{4} + \frac{1}{5} = \frac{19}{20} < 1 }

      which is the ‘second best’ attempt at getting a number that’s almost but not quite 1 as the sum of three reciprocals of integers.

      Anyway, if we have any discrete group \Gamma of the symmetry group of the hyperbolic plane we can get a Riemann surface by taking the quotient of the hyperbolic plane by the action of this \Gamma. So, the answer to your question is “yes”.

      But to get the Klein quartic this way, we shouldn’t let \Gamma be the full symmetry group of the (2,3,7) triangular tiling. Instead, we want a subgroup that’s ‘1/336 as big’, so we get a surface that has 336 of these triangles on it—and thus 56 = 336/6 of the larger ‘equilateral’ triangles shown here:

      or equivalently, the 24 = 336/14 heptagons you mentioned.

      Sorry if I’m drowning you with irrelevant detail! The point I’m trying to make is this: the tiling of hyperbolic space by triangles that comes from a solution of

      \displaystyle{ \frac{1}{a} + \frac{1}{b} + \frac{1}{c} <1}

      does not uniquely determine a Riemann surface. It has a symmetry group, and any subgroup of this symmetry group gives a Riemann surface. And I don’t understand the whole range of possibilities nearly as well as I’d like to.

      What values are possible for the genus g, i.e. number of holes?

      This is a complicated question if we fix a tiling by triangles and then ask which genuses (genii?) we can get. Over here I said that in the (2,3,7) case the first genus we can get is 3, then 7, then 13….

      Reply
      • meditationatae says:
        26 May, 2013 at 11:36 pm

        Ah… Now I understand better what you mean by 1/336 as big. You call the discrete subgroup acting on the hyperbolic plane \Gamma. Could it be that the hyperbolic plane \mathbb{H} has a so-called “fundamental domain” , say U, such that U comprises 336 triangles and \Gamma through its action on \mathbb{H} tiles the hyperbolic plane with pieces congruent to U?

        Reply
        • John Baez says:
          28 May, 2013 at 12:01 am

          Mediationatae wrote:

          Ah… Now I understand better what you mean by “1/336 as big”.

          Technically I meant that the full symmetry group of the tiling, say \Gamma', has a subgroup \Gamma of index 336. In other words, the quotient \Gamma'/\Gamma has 336 elements.

          I was avoiding math jargon since I don’t know you. But it sounds like you understand math jargon.

          Could it be that the hyperbolic plane \mathbb{H} has a so-called “fundamental domain”, say U, such that U comprises 336 triangles and \Gamma through its action on \mathbb{H} tiles the hyperbolic plane with pieces congruent to U?

          I think that’s right. Here’s what I can remember if I think hard.

          Let me restrict attention to orientation-preserving and angle-preserving maps, i.e. conformal transformations. The group \mathrm{PSL}(2,\mathbb{C}) acts on \mathbb{H} as conformal transformations via this formula:

          \displaystyle{ z \mapsto \frac{a z + b}{c z + d} }

          where

          \displaystyle{ \left( \begin{array}{cc} a & b \\ c & d \end{array}\right) }

          is any complex matrix with determinant 1.

          The group \mathrm{PSL}(2,\mathbb{C}) has a discrete subgroup \mathrm{PSL}(2,\mathbb{Z}) consisting of guys where 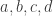a,b,c,d are integers. This in turn has a normal subgroup called \Gamma(7), consisting of guys where the entries of

          \displaystyle{ \left( \begin{array}{cc} a & b \\ c & d \end{array}\right) }

          are congruent to the entries of the identity matrix mod 7.

          The Klein quartic is the quotient space

          \mathbb{H}/\Gamma(7)

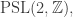          But since \Gamma(7) is a normal subgroup of \mathrm{PSL}(2,\mathbb{Z}), the quotient group

          \displaystyle{ \mathrm{PSL}(2,\mathbb{Z})/\Gamma(7) = \mathrm{PSL}(2,\mathbb{Z}/7) }

          acts as symmetries of Klein’s quartic curve. And, this group has 168 elements!

          There’s a fundamental domain for the action of \mathrm{PSL}(2,\mathbb{Z}) on Klein’s quartic curve consisting of two right triangles stuck back-to-back. We can tile Klein’s quartic curve with 168 of these triangles. I’m talking about the right triangles coming from this picture:

          But if we allow orientation-reversing angle-preserving transformations, we get a 336-element group acting on Klein’s quartic curve, namely \mathrm{PGL}(2,\mathbb{Z}), and this has a right triangle as its fundamental domain. So, we can also tile Klein’s quartic curve with 336 of these triangles.

          I know I didn’t answer your question. But I think information should help you answer your question! I’d answer it if I could, but I’m having some trouble.

  5. mitchellporter says:
    26 May, 2013 at 2:23 am

    Alejandro Rivero likes to point out that there are 96 fermionic states in the standard model, and if we treat the top as “massive” and the rest as “almost massless”, then there are 84 “almost massless” states. (A quark counts as 12 states because it’s 4 Dirac states times 3 colors.) I should ask him to comment…

    Reply
    • Alejandro Rivero says:
      26 May, 2013 at 11:22 am

      Yep, my usual remark is that there are 84 “almost massless” states, those without the top quark, and that there are also 84 “massive states”, those without the neutrino.

      But I am afraid that in my case the connection, if any, will surface via the usual representation theory, looking at the 84 states which are the source of the M2-Brane plus the other 84 which are the source of its dual, the M5-Brane. The states of the M2-Brane source are also known as the states of the antisymmetric tensor that complements the 44 degrees of freedom of the graviton in D=11, so that 84+44=128.

      Of course, it could happen that the maximality of Klein’s quartic curve and/or these sums of inverses were related to the maximality of D=11 supergravity, but I do not see how.

      Reply
  6. Graham Jones says:
    26 May, 2013 at 9:36 am

    Eric Weinstein thinks we live in a 14-dimensional observerse.

    http://www.guardian.co.uk/science/2013/may/23/eric-weinstein-answer-physics-problems
    http://www.guardian.co.uk/science/blog/2013/may/23/roll-over-einstein-meet-weinstein

    I was wondering whether to post this in the Azimuth forum (in a long-running thread), but since 42=3×14, I guess it belongs here.

    Reply
    • John Baez says:
      28 May, 2013 at 1:02 am

      I used to hang out with Eric Weinstein back in the early 90’s when I was on a 2-year leave from UCR to spend more time with Lisa in Cambridge Massachusetts. I emailed him asking for a copy of the work which started this hullabaloo (bizarrely, there seems to be no way to find out what he’s actually done). But I got a reply today saying he’d have to think about his next move.

      Reply
  7. AJ says:
    26 May, 2013 at 10:50 am

    Are these 17 ways to make three regular polygons meet snugly at a point related to the 17 possible distinct wallpaper groups?

    Reply
    • John Baez says:
      28 May, 2013 at 12:24 am

      That’s a fascinating question. The number 17 doesn’t show up all that often in math.

      I have no idea if the two appearances are related! But I have an idea for how to try to tackle this… let me try.

      Reply
      • arch1 says:
        4 June, 2013 at 8:28 pm

        John, I am leery of correcting someone who can create fascinating technical content faster and deeper than I can consume it, but if I understand the wikipedia article, the number of ways *three* regular polygons can meet is 10, while the number of ways *any number of* regular polygons can meet is 17 (21, if we distinguish between different cyclic orderings of the polygons).

        Reply
      • John Baez says:
        4 June, 2013 at 8:51 pm

        Thanks for that correction! Speed is no guarantee of accuracy. I fixed the blog article and also the longer version on my homepage.

        My attempt to link the two appearances of the number 17 hit a roadblock even before noticing this problem. There’s an interesting numerical way of showing that there are 17 wallpaper groups: it’s Conway’s Magic Theorem. However, I can’t figure out how to link this to the 17 different ways to find n whole numbers whose reciprocals add up to one less than n/2.

        By the way, the triples of regular polygons meeting snugly at a point that do give tilings of the plane:

        1/6 + 1/6 + 1/6 = 1/2
        1/4 + 1/6 + 1/12 = 1/2
        1/4 + 1/8 + 1/8 = 1/2
        1/3 + 1/12 + 1/12 = 1/2

        have a simple numerical feature in common which distinguishes them from the triples that don’t:

        1/5 + 1/5 + 1/10 = 1/2
        1/4 + 1/5 +1/20 = 1/2
        1/3 + 1/10 + 1/15 = 1/2
        1/3 + 1/9 + 1/18 = 1/2
        1/3 + 1/8 + 1/24 = 1/2
        1/3 + 1/7 + 1/42 = 1/2

        Puzzle: what is this feature and why?

        Anyone who gets stuck can read the Wikipedia article…

        Reply
  8. John Bodeen says:
    26 May, 2013 at 7:04 pm

    It’s also the only combination such that the two smaller numbers are prime

    Reply
  9. quasi says:
    26 May, 2013 at 8:06 pm

    Tutto ciò è meraviglioso. [42!]

    Reply
  10. Technology Watch says:
    26 May, 2013 at 9:21 pm

    […] 42 (wordpress.com) […]

    Reply
  11. John says:
    26 May, 2013 at 9:28 pm

    “…Felix Klein studied the most symmetrical doughnut with 3 holes. It’s a really amazing thing, called Klein’s quartic curve”

    Why does the image appear to have 4 holes?

    Reply
  12. Newt0311 says:
    26 May, 2013 at 11:49 pm

    And the fact that 42 is the ascii code for ‘*’ which has been used for decades as the shell marker for “anything and everything” surely has nothing to do with it…

    (just joking. Great article.)

    Reply
  13. some says:
    27 May, 2013 at 2:00 am

    a=1, b=2….h=8…, m=13… t=20…z=26.

    m+a+t+h = 13 + 1 + 20 + 8 = 42

    Reply
  14. tPenguinLTG says:
    27 May, 2013 at 4:09 am

    Reblogged this on `The Penguin' says… and commented:

    If I remember correctly, Douglas Adams chose ’42’ because he needed a random, unimportant-sounding, funny number. And the question? The Earth was destroyed five minutes before it could get to it.

    Reply
  15. meditationatae says:
    27 May, 2013 at 7:44 am

    Concerning the discrete subgroup of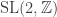 \mathrm{SL}(2,\mathbb{Z}) connected to folding the hyperbolic plane into the Klein Quartic, a 5-page document by Julia Matsieva, “The Klein Quartic”, available as a PDF download, was helpful to me.

    Reply
  16. Simon says:
    27 May, 2013 at 2:31 pm

    With a little sketch I verified that the sum of internal angels of a polygon with n corners is (n-2)\times 180 as I vaguely remembered from highschool. So the angle in the corner of a regular polygon is (1-\frac{2}{n}) \times 180 and if we attach the three polygons you suggested we get

    \frac{1}{3} \times 180 + \frac{5}{7} \times 180 + \frac{40}{42} \times 180 = 360

    This can be shown to be equivalent to your equation:

    \frac{1}{3} + \frac{1}{7} + \frac{1}{47} = \frac{1}{2}

    yet I feel like I missed the important part, did I? What is it?

    Reply
    • John Baez says:
      28 May, 2013 at 12:42 am

      Everything you did is fine… and important. But here’s the special thing about the number 42.

      There are lots of ways to write \frac{1}{2} as the sum of 3 reciprocals, and each one gives a way for 3 regular polygons to meet at a corner. For example, we have

      \frac{1}{4} + \frac{1}{8} + \frac{1}{8} = \frac{1}{2}

      and using your ideas we can rewrite this as

      \frac{2}{4} \times 180 + \frac{6}{8} \times 180 + \frac{6}{8} \times 180 = 360

      which says that the interior angles of a square and two octagons add up to 360°. So, we get this:

      Similarly,

      \frac{1}{5} + \frac{1}{5} + \frac{1}{10} = \frac{1}{2}

      gives this:

      But what’s special about 42 is that it’s the biggest number that can appear in a formula like this. So, it gives us a picture like this having a polygon with the largest possible number of sides!

      It’s a fun puzzle to show this. It’s best to try it when you’re taking a long bus ride, your flight is delayed, or you’ve been put in jail for a crime you didn’t commit. But if you get stuck and can’t do it, go here.

      Reply
  17. Baez’s “42″ – Solving the first puzzle | Spin Foam says:
    27 May, 2013 at 5:10 pm

    […] In a blog post, John Baez proposes the following puzzle: […]

    Reply
  18. Bill says:
    27 May, 2013 at 6:00 pm

    The question was “What is six times seven?” if I remember correctly. It was also the number of letters in the apology that Arthur and Ford found later. I believe this was in Life, the Universe and Everything (3rd in the trilogy) but it has been a long time since I read the series.

    Reply
    • tPenguinLTG says:
      28 May, 2013 at 2:32 am

      Actually, it was “What do you get if you multiply six by nine?”, formed by randomly picking out Scrabble tiles from a bag. This is from The Restaurant at the End of the Universe (2nd in the trilogy).
      Source

      Reply
      • GrayGaffer says:
        28 May, 2013 at 3:03 am

        Notice that 42 is also the wrong answer. Typical.

        The Scrabble scene is also the closing scene of the BBC serialized TV show.

        Reply
  19. John Baez says:
    28 May, 2013 at 12:53 am

    I almost didn’t post this blog article, because it’s so unrelated to the core mission of the Azimuth Project. But now I’m sort of glad I did, because it was the most popular article in a long time! Here’s a graph of the number of hits per hour on this blog, in the recent time period ending now:

    The usual hit rate is almost negligible compared to this spike!

    Of course it’s slightly annoying that more people are interested in jokes about the number 42 than in saving the planet. But since in the book the Earth was destroyed before anyone discovered what question had 42 as its answer, maybe there’s some connection.

    And as some cynics say, “all publicity is good publicity.”

    Reply
  20. Jon Awbrey says:
    28 May, 2013 at 2:12 am

    Here are two ways of looking at the “doubly recursive factorization” of 42.

    Details at OEIS • Riffs and Rotes

    Reply
  21. Weekly links for May 27 | God plays dice says:
    28 May, 2013 at 4:05 am

    […] John Baez on (the number) 42. […]

    Reply
  22. meditationatae says:
    28 May, 2013 at 8:16 am

    I’ve thought a bit about translations and rotations about a fixed point in the hyperbolic plane, since they probably generate the full group of orientation-preserving isometries. It seems to me that from some vantage point in the hyperbolic plane, it makes sense to think about the Horizon, and walking “straight” towards a “point” on the Horizon. But there’s something weird about “parallel” lines: instead of being a constant distance apart, in most or almost all cases they might have a “region” where their “close” whereas moving away along a parallel, we’ld see the other parallel getting increasingly distant.
    David Bernier, alias meditationatae .

    Reply
    • John Baez says:
      28 May, 2013 at 11:45 pm

      The hyperbolic plane is an example of a symmetric space. For any such space, if we fix a point and a tangent vector at that point, we get a 1-parameter group of symmetries of the space, called ‘transvections’, which are a bit like translations, and which move the chosen point in the chosen direction.

      I think these are the ‘translations’ you’re talking about. For any point in any connected symmetric space, the symmetry group of that space is generated by the rotations around that point (that is, the symmetries fixing that point), together with the transvections for that point.

      Reply
  23. John Baez says:
    28 May, 2013 at 2:32 pm

    It turns out that 42 is one of a sequence of numbers with similar properties. I learned this from a cryptic clue offered by Håkan Holgersson over on G+:

    Oh! This made me think about Cahen’s constant again. Hope it is good thing.

    Reading about Cahen’s constant on Wikipedia led me to Sylvester’s sequence. Here’s the deal.

    Let’s use a ‘greedy algorithm’ to seek Egyptian fractions—that is, sums of reciprocals of positive integers—that are close to 1.

    So, we start writing down a sequence of Egyptian fractions where at each stage we add a new term chosen to be as large as possible while still keeping the sum smaller than 1:

    \displaystyle{ \frac{1}{2} < 1 }

    \displaystyle{ \frac{1}{2} + \frac{1}{3} < 1 }

    \displaystyle{ \frac{1}{2} + \frac{1}{3} + \frac{1}{7} < 1 }

    \displaystyle{ \frac{1}{2} + \frac{1}{3} + \frac{1}{7} + \frac{1}{43} < 1 }

    \displaystyle{ \frac{1}{2} + \frac{1}{3} + \frac{1}{7} + \frac{1}{43} + \frac{1}{1807} < 1 }

    etcetera.

    The first interesting fact is that if at any stage we subtract one from the last denominator, we get an Egyptian fraction that sums to 1:

    \displaystyle{ \frac{1}{1} = 1 }

    \displaystyle{ \frac{1}{2} + \frac{1}{2} = 1}

    \displaystyle{ \frac{1}{2} + \frac{1}{3} + \frac{1}{6} = 1 }

    \displaystyle{ \frac{1}{2} + \frac{1}{3} + \frac{1}{7} + \frac{1}{42} = 1}

    \displaystyle{ \frac{1}{2} + \frac{1}{3} + \frac{1}{7} + \frac{1}{43} + \frac{1}{1806} = 1}

    etcetera.

    The second interesting fact is that this sequence of numbers, called Sylvester’s sequence:

    s_0 = 2, s_1 = 3, s_2 = 7, s_3 = 43, s_4 = 1807, s_5 = 3263443, \dots

    has a simple recursive definition. Namely, each term is 1 more than the product of all the previous terms!

    \displaystyle{ s_{n+1} = 1 + \prod_{i = 0}^{n} s_i }

    Equivalently,

    \displaystyle{ s_{n+1} = s_n(s_n - 1) + 1 }

    Sylvester’s sequence has various interesting mathematical properties. But, I don’t know if any of the interesting geometrical properties of the number 42, described in this blog entry, generalize to other Sylvester numbers. Anyone know anything good about 1806?

    Reply
    • AJ says:
      28 May, 2013 at 3:48 pm

      The numbers 2, 6, 42 and 1806 are all “primary pseudoperfect numbers”. The interesting thing is that only these first four primary pseudoperfect numbers correspond to the first four numbers in Sylvester’s sequence, which brings us to “Znám’s problem”, that has been proven to be unsolvable for exactly the first 4 numbers of Sylvester’s sequence (while it is solvable for each k ≥ 5).

      I wonder whether this could again be connected to “Hurwitz’s theorem” and its 4 dimensions (as opposed to “Hurwitz’s automorphisms theorem” that is referenced above).

      Reply
    • Greg Egan says:
      28 May, 2013 at 11:00 pm

      Suppose you want the internal angles between the edges of your polygons to add up to a positive integer multiple of 360 degrees. If you have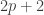 2p+2 reciprocals that sum to 1, and one of those reciprocals is \frac{1}{2}, you can fit vertices of polygons with all the other denominators as their numbers of sides together so that they sum to p full rotations.

      So for example, for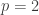 p=2, 2p+2=6, using the second through sixth terms of Sylvester’s sequence you could fit a triangle, a heptagon, a 43-gon, an 1807-gon and a 3,263,442-gon (subtracting 1 from the last term) together to form a local double cover of the flat plane.

      I wonder if you could get some kind of interesting hyperbolic Riemann surface by omitting one of the polygons, as you can with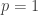 p=1.

      Reply
  24. Blake Stacey says:
    28 May, 2013 at 2:54 pm

    Hmmm.

    \displaystyle \frac{1}{a} + \frac{1}{b} + \frac{1}{c} < 1

    gives a triangular tiling of hyperbolic space, while

    \displaystyle \frac{1}{a} + \frac{1}{b} + \frac{1}{c} > 1

    gives the ADE classification. (See Eq. (21) of Capelli and Zuber (2009).)

    Reply
    • John Baez says:
      29 May, 2013 at 12:39 am

      Yes! I wrote a lot about this in week182 of This Week’s Finds. I’m trying to gradually gather all my Egyptian fraction material in one place and integrate the exposition. Right now it’s in 3 places:

      • Archimedean tilings and Egyptian fractions.

      • week182: ADE classifications, Egyptian fractions and tilings of the plane, sphere and hyperbolic plane.

      • 42: the special role of the number 42.

      The last one has a big appendix at the end, not included in this blog article.

      Reply
  25. David Harden says:
    22 June, 2013 at 8:11 pm

    When you say 1092 symmetries, do those form a group isomorphic to PSL(2,13)? That group is interesting because it’s the smallest finite simple nonabelian group which isn’t factorable:

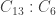    A finite group G is called factorable if G = HK where H and K are both proper subgroups of G. If G is factorable, H and K may be assumed, without loss of generality, to be maximal subgroups of G. But the maximal subgroups of PSL(2,13) are isomorphic to A_{4} , C_{13}:C_6 , and dihedral groups of order 12 or 14. The only possibility that might work out, order-wise, is C_13:C_6 and a dihedral group of order 14 — but these contain an element of order 2 in common, so factorability fails.

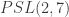    Any transitive permutation group on a prime-power number of points (say it’s a power of the prime p) which is not cyclic is factorable, since H may be chosen to be a point stabilizer and K may be chosen to be a Sylow p-subgroup of G. This covers the nonabelian simple groups A_5 (transitive on 5 points), PSL(2,7) (transitive on 7 or 8 points), PSL(2,8) (transitive on 9 points), and PSL(2,11) (transitive on 11 points). For A_6 , both H and K can be chosen to be isomorphic to A_5 (so then any automorphism of A_6 taking H to K is outer, as an automorphism of S_6 ).

    Factorability is interesting for those of us who want to find newer (and maybe easier) proofs of statements — such as a proof of the conjugacy of complements in Schur-Zassenhaus which avoids the appeal to the Odd Order Theorem. I think a minimal (in terms of the order of the complement) counterexample has unfactorable complements, though I need to be more careful before asserting that.

    Reply
  26. 42 | Third Perspective says:
    17 May, 2014 at 4:50 am

    42

    The answer for life, universe and everything. Since long people believed that Douglas Adams had just made that up, but that was not the case. The guy was truly a genius, and that is what I am going to write here. […]

    Reply

You can use Markdown or HTML in your comments. You can also use LaTeX, like this: $latex E = m c^2 $. The word 'latex' comes right after the first dollar sign, with a space after it.

This site uses Akismet to reduce spam. Learn how your comment data is processed.