Large Countable Ordinals (Part 2)

Last time I took you on a road trip to infinity. We zipped past a bunch of countable ordinals

$\omega , \; \omega^\omega,\; \omega^{\omega^\omega}, \;\omega^{\omega^{\omega^\omega}}, \dots$

and stopped for gas at the first one after all these. It’s called $\epsilon_0.$ Heuristically, you can imagine it like this:

$\epsilon_0 = \omega^{\omega^{\omega^{\omega^{\cdot^{\cdot^{\cdot}}}}}}$

More rigorously, it’s the smallest ordinal $x$ obeying the equation

$x = \omega^x$

Beyond ε_o

But I’m sure you have a question. What comes after $\epsilon_0$ ?

Well, duh! It’s

$\epsilon_0 + 1$

Then comes

$\epsilon_0 + 2$

and then eventually we get to

$\epsilon_0 + \omega$

and then

$\epsilon_0 + \omega^2 ,\dots, \epsilon_0 + \omega^3,\dots \epsilon_0 + \omega^4,\dots$

and after a long time

$\epsilon_0 + \epsilon_0 = \epsilon_0 2$

and then eventually

$\epsilon_0^2$

and then eventually….

Oh, I see! You wanted to know the first really interesting ordinal after $\epsilon_0.$

Well, this is a matter of taste, but you might be interested in $\epsilon_1.$ This is the first ordinal after $\epsilon_0$ that satisfies this equation:

$x = \omega^x$

How do we actually reach this ordinal? Well, just as $\epsilon_0$ was the limit of this sequence:

$\omega , \; \omega^\omega,\; \omega^{\omega^\omega}, \;\omega^{\omega^{\omega^\omega}}, \dots$

$\epsilon_1$ is the limit of this:

$\epsilon_0 + 1, \; \omega^{\epsilon_0 + 1}, \; \omega^{\omega^{\epsilon_0 + 1}}, \; \omega^{\omega^{\omega^{\epsilon_0 + 1}}},\dots$

You may wonder what I mean by the ‘limit’ of an increasing sequence of ordinals. I just mean the smallest ordinal greater than or equal to every ordinal in that sequence. Such a thing is guaranteed to exist, since if we treat ordinals as well-ordered sets, we can just take the union of all the sets in that sequence.

Here’s a picture of $\epsilon_1,$ taken from David Madore’s interactive webpage:

In what sense is $\epsilon_1$ the first "really interesting" ordinal after $\epsilon_0$ ?

For one thing, it’s first that can’t be built out of $1, \omega$ and $\epsilon_0$ using finitely many additions, multiplications and exponentiations. In other words, if we use Cantor normal form to describe ordinals (as explained last time), and allow expressions involving $\epsilon_0$ as well as $1$ and $\omega,$ we get a notation for all ordinals up to $\epsilon_1.$

What’s the next really interesting ordinal after $\epsilon_1$ ? As you might expect, it’s called $\epsilon_2.$ This is the next solution of

$x = \omega^{x}$

and it’s defined to be the limit of this sequence:

$\epsilon_1 + 1, \; \omega^{\epsilon_1 + 1}, \;\omega^{\omega^{\epsilon_1 + 1}}, \; \omega^{\omega^{\omega^{\epsilon_1 + 1}}},\dots$

Maybe now you get the pattern. In general, $\epsilon_{\alpha}$ is the
$\alpha$ th solution of $x = \omega^{x}.$ We can define this, if we’re smart, for any ordinal $\alpha.$

So, we can keep driving on through fields of ever larger ordinals:

$\epsilon_2,\dots, \epsilon_{3},\dots, \epsilon_{4}, \dots$

and eventually

$\epsilon_{\omega}$

which is the first ordinal bigger than $\epsilon_0, \epsilon_1, \epsilon_2, \dots$

Let’s stop and take a look!

Nice! Okay, back in the car…

$\epsilon_{\omega+1},\dots, \epsilon_{\omega+2},\dots, \epsilon_{\omega+1},\dots$

and then

$\epsilon_{\omega^2},\dots , \epsilon_{\omega^3},\dots, \epsilon_{\omega^4},\dots$

and then

$\epsilon_{\omega^{\omega}},\dots, \epsilon_{\omega^{\omega^{\omega}}},\dots$

As you can see, this gets boring after a while: it’s suspiciously similar to the beginning of our trip through the ordinals. The same ordinals are now showing up as subscripts in this epsilon notation. But we’re moving much faster now, since I’m skipping over much bigger gaps, not bothering to mention all sorts of ordinals like

$\epsilon_{\omega^{\omega}} + \epsilon_{\omega 248} + \omega^{\omega^{\omega + 17}} + 1$

Anyway… while we’re zipping along, I might as well finish telling you the story I started last time. My friend David Sternlieb and I were driving across South Dakota on Route 80. We kept seeing signs for the South Dakota Tractor Museum. When we finally got there, we were driving pretty darn fast, out of boredom—about 85 miles an hour. And guess what happened then!

Oh — wait a minute—this one is sort of interesting:

$\displaystyle{ \epsilon_{\epsilon_0} }$

Then come some more like that:

$\epsilon_{\epsilon_1},\dots, \epsilon_{\epsilon_2},\dots \epsilon_{\epsilon_3},\dots$

until we reach this:

$\epsilon_{\epsilon_{\omega}}$

and then

$\epsilon_{\epsilon_{\omega^{\omega}}},\dots, \epsilon_{\epsilon_{\omega^{\omega^{\omega}}}},\dots$

As we keep speeding up, we see:

$\epsilon_{\epsilon_{\epsilon_0}},\dots \epsilon_{\epsilon_{\epsilon_{\epsilon_0}}},\dots \epsilon_{\epsilon_{\epsilon_{\epsilon_{\epsilon_0}}}},\dots$

So, anyway: by the time we got that tractor museum, we were driving really fast. And, all we saw as we whizzed by was a bunch of rusty tractors out in a field! It was over in a split second! It was a real anticlimax — just like this anecdote, in fact.

But that’s just the way it is when you’re driving through these ordinals! Every ordinal, no matter how large, looks pretty pathetic and small compared to the ones ahead — so you keep speeding up, looking for something ‘really new and different’. But when you find one, it turns out to be part of a larger pattern, and soon that gets boring too.

For example, when we reach the limit of this sequence:

$\epsilon_0, \epsilon_{\epsilon_0}, \epsilon_{\epsilon_{\epsilon_0}}, \epsilon_{\epsilon_{\epsilon_{\epsilon_0}}}, \epsilon_{\epsilon_{\epsilon_{\epsilon_{\epsilon_0}}}},\dots$

our notation fizzles out again, since this is the first solution of

$x = \epsilon_{x}$

We could make up a new name for this ordinal, like $\zeta_0.$ I don’t think this name is very common, though I’ve seen it. We could call it the Tractor Museum of Countable Ordinals.

Now we can play the whole game again, defining the zeta number $\zeta_{\alpha}$ to be the $\alpha$ th solution of

$x = \epsilon_x$

sort of like how we defined the epsilons. This kind of equation, where something equals some function of itself, is called a fixed point equation.

But since we’ll have to play this game infinitely often, we might as well be more systematic about it!

The Veblen hierarchy

As you can see, we keep running into new, qualitatively different types of ordinals. First we ran into the powers of omega. Then we ran into the epsilons, and then the zetas. It’s gonna keep happening! For each type of ordinal, our notation fizzles out when we reach the first ‘fixed point’— when the xth ordinal of this type is actually equal to x.

So, instead of making up infinitely many Greek letters for different types of ordinals let’s index them… by ordinals! For each ordinal $\gamma$ we’ll have a type of ordinal. We’ll let $\phi_\gamma(\alpha)$ be the $\alpha$ th ordinal of type $\gamma.$

We can use the fixed point equation to define $\phi_{\gamma+1}$ in terms of $\phi_{\gamma}.$ In other words, we start off by defining

$\phi_0(\alpha) = \omega^{\alpha}$

and then define

$\phi_{\gamma+1}(\alpha)$

to be the $\alpha$ th solution of

$x = \phi_{\gamma}(x)$

where we start counting at $\alpha = 0,$ so the first solution is called the ‘zeroth’.

We can even make sense of $\phi_\gamma(\alpha)$ when $\gamma$ itself is infinite! Suppose $\gamma$ is a limit of smaller ordinals. Then we define $\phi_\gamma(x)$ to be the limit of $\phi_\beta(x)$ as $\beta$ approaches $\gamma.$ I’ll make this more precise next time.

We get infinitely many different types of ordinals, called the Veblen hierarchy. So, concretely, the Veblen hierarchy starts with the powers of $\omega:$

$\phi_0(\alpha) = \omega^\alpha$

and then it goes on to the ‘epsilons’:

$\phi_1(\alpha) = \epsilon_\alpha$

and then it goes on to what I called the ‘zetas’:

$\phi_2(\alpha) = \zeta_\alpha$

But that’s just the start!

The Feferman–Schütte ordinal

Boosting the subscript $\gamma$ in $\phi_\gamma(\alpha)$ increases the result much more than boosting $\alpha,$ so let’s focus on that and just let $\alpha = 0.$ The Veblen hierarchy contains ordinals like this:

$\phi_{\omega}(0), \; \phi_{\omega+1}(0), \; \phi_{\omega+2}(0), \dots$

and then ordinals like this:

$\phi_{\omega^2}(0), \; \phi_{\omega^3}(0), \; \phi_{\omega^4}(0), \dots$

and then ordinals like this:

$\phi_{\omega^\omega}(0), \; \phi_{\omega^{\omega^\omega}}(0), \; \phi_{\omega^{\omega^{\omega^{\omega}}}}(0), \dots$

and then this:

$\phi_{\epsilon_0}(0), \phi_{\epsilon_{\epsilon_0}}(0), \phi_{\epsilon_{\epsilon_{\epsilon_0}}}(0), \dots$

where of course I’m skipping huge infinite stretches of ‘boring’ ones. But note that

$\phi_{\omega}(0) = \phi_{\phi_0(0)}(0)$

and

$\phi_{\epsilon_0}(0) = \phi_{\phi_1(0)}(0)$

and

$\phi_{\zeta_0}(0) = \phi_{\phi_2(0)}(0)$

In short, we can plug the phi function into itself—and we get the biggest effect if we plug it into the subscript!

So, if we’re in a rush to reach some really big countable ordinals, we can try these:

$\phi_0(0), \; \phi_{\phi_0(0)}(0) , \; \phi_{\phi_{\phi_0(0)}(0)}(0), \dots$

But the limit of these is an ordinal $x$ that has

$x = \phi_x(0)$

This is called the Feferman–Schütte ordinal and denoted $\Gamma_0.$

In fact, the Feferman–Schütte ordinal is the smallest solution of

$x = \phi_x(0)$

Since this equation is self-referential, we can’t describe Feferman–Schütte ordinal using the Veblen hierarchy—at least, not without using the Feferman–Schütte ordinal!

Indeed, some mathematicians have made a big deal about this ordinal, claiming it’s

the smallest ordinal that cannot be described without self-reference.

This takes some explaining, and it’s somewhat controversial. After all, there’s a sense in which every fixed point equation is self-referential. But there’s a certain precise sense in which the Feferman–Schütte ordinal is different from previous ones.

Anyway, you have admit that this is a very cute description of the Fefferman–Schuette ordinal: “the smallest ordinal that cannot be described without self-reference.” Does it use self-reference? It had better—otherwise we have a contradiction!

It’s a little scary, like this picture:

More importantly for us, the Veblen hierarchy fizzles out when we hit the Feferman–Schuette ordinal. Let me say what I mean by that.

Veblen normal form

The Veblen hierarchy gives a notation for ordinals called the Veblen normal form. You can think of this as a high-powered version of Cantor normal form, which we discussed last time.

Veblen normal form relies on this result:

Theorem. Any ordinal $\beta$ can be written uniquely as

$\beta = \phi_{\gamma_1}(\alpha_1) + \dots + \phi_{\gamma_{k}}(\alpha_k)$

where $k$ is a natural number, each term is less than or equal to the previous one, and $\alpha_i < \phi_{\gamma_i}(\alpha_i)$ for all $i.$

Note that we can also use this theorem to write out the ordinals $\beta_i$ and $\gamma_i$ , and so on, recursively. So, it gives us a notation for ordinals.

However, this notation is only useful when all the ordinals $\alpha_i, \gamma_i$ are less than the ordinal $\beta$ that we’re trying to describe. Otherwise we need to already have a notation for $\beta$ to express $\alpha$ in Veblen normal form!

So, the power of this notation eventually fizzles out. And the place where it does is Feferman–Schütte ordinal. Every ordinal less than this can be expressed in terms of $0$ , addition, and the function $\phi,$ using just finitely many symbols!

The moral

As I hope you see, the power of the human mind to see a pattern and formalize it gives the quest for large countable ordinals a strange quality. As soon as we see a systematic way to generate a sequence of larger and larger ordinals, we know this sequence has a limit that’s larger then all of those! And this opens the door to even larger ones….

So, this whole journey feels a bit like trying to outrace our car’s own shadow as we drive away from the sunset: the faster we drive, the faster it shoots ahead of us. We’ll never win.

On the other hand, we’ll only lose if we get tired.

So it’s interesting to hear what happens next. We don’t have to give up. The usual symbol for the Feferman–Schütte ordinal should be a clue. It’s called $\Gamma_0.$ And that’s because it’s just the start of a new series of even bigger countable ordinals!

I’m dying to tell you about those. But this is enough for today.

This entry was posted on Monday, July 4th, 2016 at 1:00 am and is filed under mathematics. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.

46 Responses to Large Countable Ordinals (Part 2)

Marek14 says:

4 July, 2016 at 4:32 am

A question that comes in mind is: can we actually find any example of an ordered set corresponding to such ordinals, OTHER than the ordinal itself? For example, a set of all natural numbers, followed by set of all pairs in lexicographic order, then all triplets, quadruplets, etc… is still just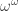 $\omega^\omega$ . To get to epsilon, we could imagine similar lexicographic ordering of finite sequences of finite sequences, and of finite sequences of finite sequences of finite sequences, up to arbitrarily many levels of nesting, But beyond that…

Reply
- John Baez says:
  
  4 July, 2016 at 4:59 am
  
  There’s an order-preserving isomorphism between the set ordinals up to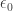 $\epsilon_0$ and the set of finite rooted trees, with a certain nice ordering on them. This is the basis of the hydra game, which you can play online here if you can convince your browser it’s safe to run this Java applet. (I promise: it’s safe.)
  
  It’s also possible to explicitly describe a subset of the real line which, with the usual ordering, is isomorphic to the set of ordinals up to $\epsilon_0.$ That’s how David Madore drew the picture here:
  
  Click on the picture, and then click on the names of ordinals, to explore this further.
  
  However, I don’t know if you’ll consider these structures to be different from “the ordinal itself”. Whenever two mathematical structures are isomorphic, it’s a bit subjective to decide whether they are “the same” or “different”.
  
  I should add that the main use, so far, of countable ordinals above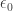 $\epsilon_0$ is to measure the strength of axiom systems. You can see an explanation and lots of examples here:
  
  • Wikipedia, Ordinal analysis.
  
  Proof theorists keep needing larger countable ordinals to measure the strength of stronger axiom systems! For example, it seems nobody has yet found a good notation for countable ordinals large enough to measure the strength of Zermelo—Fraenkel set theory:
  
  • Scott Aaronson, Is there a computable ordinal encoding the proof strength of ZF? Is it knowable?, MathOverflow, 26 April 2014.
  
  Henry Towsner’s short answer is:
  
  Finding an explicit description of the ordinal for ZFC is an active problem in proof theory, but progress has been very slow..
  
  Reply
  - Marek14 says:
    
    4 July, 2016 at 5:19 am
    
    Well, for the subset of real line, the question is whether each ordinal can be actually assigned a specific real number. A picture by itself isn’t much.
    
    If you have an interval, then you can put omega in it by filling it with an infinite sequence — for <0,1), the sequence of 0, 1/2, 3/4, 7/8, etc. would be sufficient.
    
    To get omega^2, you’d iterate this, putting another omega-worth to intervals <0,1/2), <1/2,3/4), <3/4,7/8), etc. For omega^omega, you’d fit omega into <0,1/2), omega^2 into <1/2, 3/4), omega^3 into <3/4,7/8), etc. But can the above definition of epsilon give an explicit assignment of a real (well, rational, probably) number for every ordinal below epsilon?
    
    Reply
    - Royce Peng says:
      
      4 July, 2016 at 7:33 am
      
      I actually wrote an answer to this question on Math Stack Exchange: see
      
      http://math.stackexchange.com/questions/165151/question-of-an-isomorphism-of-epsilon-0-and-a-subset-of-the-rationals/200616#200616.
      
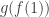      It turns out, though, that any countable ordinal can be embedded into the rationals! Given a countable ordinal $\alpha$ , we can define a bijection $f:\mathbb{N} \mapsto \alpha$ . Start by setting $g(f(0)) = \frac{1}{2}$ . Set $g(f(1))$ to either 1/4 or 3/4, depending on whether or not 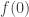$f(0)$ is bigger than 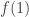$f(1)$ . Say it is bigger. Then set $g(f(2))$ to be either 1/4 if it f(2) is less than f(0), 5/8 if f(2) is between f(0) and f(1), and 7/8 if f(2) is bigger than f(1). 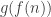And just continue in that fashion: each time, set $g(f(n))$ in the middle of the interval where f(n) is supposed to be (considering 0 and 1 to be -infinity and infinity). At the end you will have the ordinal $\alpha$ represented as a set of dyadic rationals betwen 0 and 1.
      
      What about uncountable ordinals? Unfortunately, those cannot be embedded in the real numbers; after each ordinal, there is a next one, which must be some positive distance to the right. So if we could embed an uncountable ordinal in the real numbers, to each ordinal in the set we could associate a rational number in the interval between that ordinal and the next. But there are only countably many rational numbers, a contradiction.
  - John Baez says:
    
    4 July, 2016 at 7:06 am
    
    Marek14 wrote:
    
    But can the above definition of epsilon give an explicit assignment of a real (well, rational, probably) number for every ordinal below epsilon?
    
    Yes, there are various explicit ways to do this. To see one way, click on this:
    
    and then type “CTRL-u” to see the Javascript program that drew the picture. But personally, since I don’t read Javascript very well, I’d find it more fun to make up my own way!
    
    Reply
- John Baez says:
  
  4 July, 2016 at 7:27 am
  
  Oh, and here’s another way to get a well-ordered set that’s isomorphic to a fairly large ordinal.
  
  Consider all functions
  
  $f \colon [1,\infty) \to [1,\infty)$
  
  built up from the functions $1$ and $x$ by addition, multiplication and exponentiation. So, functions like this:
  
  $\displaystyle{ x^{x^{x + x} + x} x + x + x + 1 }$
  
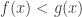  Say $f < g$ if $f(x) < g(x)$ for all sufficiently large $x.$ In 1973 Ehrenfeucht proved this ordering was a well-ordering. So, this set of functions, with this ordering, corresponds to some ordinal.
  
  Which ordinal? Skolem proved that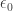 $\epsilon_0$ is a lower bound. In 1978, Levitz proved that 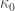$\kappa_0$ is an upper bound.
  
  Skolem guessed that the right answer is $\epsilon_0.$ This certainly seems like the obvious guess, given how these functions:
  
  $x^{x^x} x + x + x + 1$
  
  look a lot like the ordinals below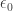 $\epsilon_0$ :
  
  $\omega^{\omega^\omega} \omega + \omega + \omega + 1$
  
  Reply
  - Royce Peng says:
    
    4 July, 2016 at 7:49 am
    
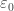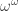    Yep, that leads to the trivial lower bound of $\varepsilon_0$ . The partial results of Levitz, Van den Dries and Dahn are (or at least include) $2^x$ corresponds to $\omega^\omega$ (this is very easy), and that 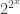$2^{2^x}$ corresponds to 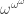$\omega^{\omega^\omega}$ . (This is probably less easy.)
    
    But wait, wasn’t the upper bound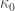 $\kappa_0$ and not $\kappa_1$ ?
    
    Reply
    - Royce Peng says:
      
      4 July, 2016 at 8:01 am
      
      Whoops, I keep forgetting to write “latex”. Is there a way to edit posts?
    - John Baez says:
      
      4 July, 2016 at 8:15 am
      
      Alas, no. But the management usually fixes things.
  - John Baez says:
    
    4 July, 2016 at 7:58 am
    
    Sorry, I meant $\kappa_0.$ Fixed.
    
    I also introduced a mistake when I misunderstood the result in this paper:
    
    • Lou van Dries and Hilbert Levitz, On Skolem’s exponential functions below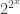 $2^{2^x}$ , Trans. Amer. Math. Soc. 286 (1984), 339–349.
    
    I’ve fixed that now.
    
    Reply
- Royce Peng says:
  
  4 July, 2016 at 8:39 am
  
  Another very nice well-ordered set are the “Fusible numbers”. See here: http://www.mathpuzzle.com/fusible.pdf for a very nice presentation of the fusible numbers, although a couple of things in the slides are incorrect.
  
  Basically, the idea is that you have an infinite set of fuses that each take 1 hour to burn, and the fusible numbers are those numbers of hours that you can time by burning the fuses in various ways. So you can time 1/2 hour by light a single fuse at one end. You can time 3/4 of an by lighting fuse 1 at both ends and fuse 2 at one end at time 0, and lighting the other end of fuse 2 when fuse 1 burns out.
  
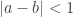  Mathematically the fusible numbers are defined as the smallest set which contains 0 and is closed under the operation $a,b \mapsto \frac{a+b+1}{2}$ provided that $|a-b| < 1$ . This correpsonds to lighting one end of a fuse at time a and the other at time b, so it will burn out at time $\frac{a+b+1}{2}.$
  
  A relatively simple argument proves that the fusible numbers are well-ordered, so again we can ask what ordinal the fusible numbers correspond to. We can identify a subset of the fusible numbers with order type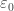 $\varepsilon_0$ , so that is a lower bound for the order type of the entire set. It is conjectured that the order type is exactly 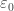$\varepsilon_0$ , but we don’t know for sure; so the situation is much like the situation for the problem of Skolem.
  
  Another interesting fact about fusible numbers: If we define $a(x)$ as the next fusible number after x, and 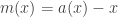$m(x) = a(x) - x$ , then m(x) will be a power of 1/2 (when x is a fusible number). So if we let $f(x) = -\log_2 (m(x))$ and focus on when x is a natural number, f(x) will be a very fast-growing function of x. 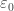If a conjecture by Junyan Xu for the fusible numbers is true, then the fusible numbers will have order type $\varepsilon_0$ and it appears that f will grow at the rate close to $F_{\varepsilon_0}(x)$ , where F is the fast-growing hierarchy. 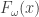This is a very fast-growing function; $F_\omega (x)$ already grows a rate equal to the Ackermann function!
  
  If Xu’s conjecture is false, then the order type of the fusible numbers could be larger, and the function f could grow even faster.
  
  Reply
  - John Baez says:
    
    4 July, 2016 at 9:16 am
    
    Cool! It’s always fun to see very fast-growing functions “in nature”.
    
    Reply
John Baez says:

4 July, 2016 at 5:03 am

Here are some puzzles in ordinal arithmetic. If you’re a super-expert, maybe you should let other people try them:

Puzzle 1. What is $\omega^{\epsilon_0}$ ?

Puzzle 2. What is ${\epsilon_0}^\omega$ ?

Puzzle 3. What is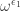 $\omega^{\epsilon_1}$ ?

Puzzle 4. What is ${\epsilon_1}^\omega$ ?

Puzzle 5. What is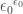 ${\epsilon_0}^{\epsilon_0}$ ?

Puzzle 6. What is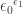 ${\epsilon_0}^{\epsilon_1}$ ?

Puzzle 7. What is ${\epsilon_1}^{\epsilon_0}$ ?

Puzzle 8. What is ${\epsilon_1}^{\epsilon_1}$ ?

Reply
- Marek14 says:
  
  4 July, 2016 at 5:29 am
  
  Well, let’s see…
  
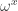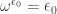  1 and 3 are trivial. Epsilons are fixed points of $\omega^x$ , so $\omega^{\epsilon_0} = \epsilon_0$ and $\omega^{\epsilon_1} = \epsilon_1$ .
  
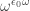  2 and 4: ${\epsilon_0}^\omega$ is ${\omega^{\epsilon_0}}^\omega$ , or $\omega^{{\epsilon_0}+1}$ , similarly ${\epsilon_1}^\omega$ is $\omega^{{\epsilon_1}+1}$ .
  
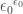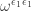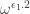  5 and 8: Similarly, we get that ${\epsilon_0}^{\epsilon_0}$ is ${\omega^{\epsilon_0}}^{\epsilon_0}$ , or $\omega^{{\epsilon_0}.2}$ and ${\epsilon_1}^{\epsilon_1}$ is ${\omega^{\epsilon_1}}^{\epsilon_1}$ , or $\omega^{{\epsilon_1}.2}$ .
  
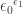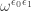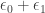  6: ${\epsilon_0}^{\epsilon_1}$ is is ${\omega^{\epsilon_0}}^{\epsilon_1}$ , or $\omega^{{\epsilon_0}+{\epsilon_1}}$ – but ${\epsilon_0}+{\epsilon_1}$ is simply ${\epsilon_1}$ , so it’s $\omega^{{\epsilon_1}}$ , or simply ${\epsilon_1}$ .
  
  7: Through analogical construction, we get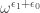 $\omega^{{\epsilon_1}+{\epsilon_0}}$ . We can’t simplify ${\epsilon_1}+{\epsilon_0}$ any further, so we probably can’t get a more succinct representation.
  
  Reply
  - Royce Peng says:
    
    4 July, 2016 at 6:10 am
    
    2, 4, 5, 7, and 8 aren’t quite right, unless you switch at some point from talking about the ordinal to talking about the exponent.
    
    Reply
    - Marek14 says:
      
      4 July, 2016 at 7:41 am
      
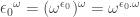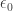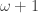
      Yeah, that was incorrect. ${\epsilon_0}^\omega = (\omega^{\epsilon_0})^\omega = \omega^{{\epsilon_0}.\omega}$ . If $\epsilon_0$ is an exponential tower of $\omega$ $\omega$ ‘s, then this is a tower of $\omega+1$ $\omega$ ‘s. So, for 4, we get
      
      $\omega^{{\epsilon_1} \cdot \omega}$
      
      for 5 we get
      
      $\displaystyle{ \omega^{{\epsilon_0}^2} }$
      
      for 8
      
      $\omega^{{\epsilon_1}^2}$
      
      and for 7
      
      $\omega^{{\epsilon_1} \cdot {\epsilon_0}}.$
      
      I made a mistake in 6 as well, but the final result should still stay since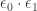 ${\epsilon_0}\cdot{\epsilon_1}$ should still equal $\epsilon_1$ .
    - Royce Peng says:
      
      4 July, 2016 at 7:53 am
      
      Correct, but those are not in (iterated) Cantor Normal Form; you have to keep going until you everything is either addition or exponentiation with base $\omega$ .
    - Marek14 says:
      
      4 July, 2016 at 7:57 am
      
      Not sure how to do that — after all, they all involve epsilons; aren’t Cantor Normal forms of epsilons already infinite? I could iterate it like that, but I’m not sure how to write the result; never used LaTeX before today, though it’s similar to equation tools in some text editors I used when translating books in the past.
    - Royce Peng says:
      
      4 July, 2016 at 8:05 am
      
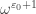      Indeed, the epsilon numbers cannot be reduced, so you just leave them as they are. However, numbers like $\varepsilon_0 \cdot \omega$ are not epsilon numbers, so they should be reduced (in this case to $\omega^{\varepsilon_0 + 1}$ ).
    - John Baez says:
      
      4 July, 2016 at 8:09 am
      
      I described Cantor normal form last time:
      
      Theorem. Every ordinal $\alpha$ can be uniquely written as
      
      $\alpha = \omega^{\beta_1} c_1 + \omega^{\beta_2}c_2 + \cdots + \omega^{\beta_k}c_k$
      
      where $k$ is a natural number, $c_1, c_2, \ldots, c_k$ are positive integers, and $\beta_1 > \beta_2 > \cdots > \beta_k \geq 0$ are ordinals.
      
      This works for every ordinal, but if you apply it to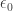 $\epsilon_0$ you get
      
      $\epsilon_0 = \omega^{\epsilon_0}$
      
      which isn’t very helpful. So, we can agree to leave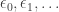 $\epsilon_0, \epsilon_1, \dots$ alone instead of applying this theorem to them. However, the theorem says we can always take expressions like
      
      ${\epsilon_0}^\omega$
      
      or
      
      $\epsilon_0 \,\omega$
      
      and rewrite them using the theorem.
      
      Of course the proof of the theorem is more informative than the mere statement of the theorem, since it says how to rewrite these expressions!
    - Marek14 says:
      
      4 July, 2016 at 8:18 am
      
      OK, so if we use normal form with epsilons, we have:
      
      Puzzle 1.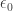 $\epsilon_0$
      
      Puzzle 2. $\omega^{\omega^{{\epsilon_0}+1}}$
      
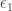
      Puzzle 3. $\epsilon_1$
      
      Puzzle 4. $\omega^{\omega^{{\epsilon_1}+1}}$
      
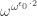
      Puzzle 5. $\omega^{\omega^{{\epsilon_0}\cdot 2}}$
      
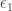
      Puzzle 6. $\epsilon_1$
      
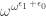
      Puzzle 7. $\omega^{\omega^{{\epsilon_1}+{\epsilon_0}}}$
      
      Puzzle 8. $\omega^{\omega^{{\epsilon_1} \cdot 2}}$
    - Royce Peng says:
      
      4 July, 2016 at 8:22 am
      
      Correct!
- Rob Superty says:
  
  4 July, 2016 at 8:34 am
  
  Hi – I’d like to give it a shot.
  
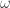  So firstly, when counting up with ordinals, I find it handy to avoid forms like $\varepsilon_0^2$ and instead to think of everything in powers of $\omega$ unless at a fixed point of 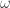$\omega$ (i.e., a pure epsilon number).
  
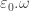  So that means when getting up through the ordinals $\varepsilon_0.2$ , $\varepsilon_0.3$ , …, I would stop at $\varepsilon_0.\omega$ and instead express that as 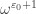$\omega^{\varepsilon_0+1}$ , because it is the next power of 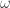$\omega$ after the first fixed point, $\varepsilon_0=\omega^{\varepsilon_0}$ . Just feels a bit tidier to me.
  
  So that being said, I’d express those 8 expressions as powers of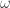 $\omega$ unless they are epsilon numbers. My answers are as follows:
  
  1) $\omega^{\varepsilon_0} = \varepsilon_0$
  2) $\varepsilon_0^\omega = (\omega^{\varepsilon_0})^\omega = \omega^{\omega^{\varepsilon_0+1}}$
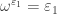
  3) $\omega^{\varepsilon_1} = \varepsilon_1$
  4) $\varepsilon_1^\omega = (\omega^{\varepsilon_1})^\omega = \omega^{\omega^{\varepsilon_1+1}}$
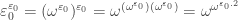
  5) $\varepsilon_0^{\varepsilon_0} = (\omega^{\varepsilon_0})^{\varepsilon_0}=\omega^{(\omega^{\varepsilon_0})}{^{(\omega^{\varepsilon_0})}}=\omega^{\omega^{\varepsilon_0.2}}$
  6) $\varepsilon_0^{\varepsilon_1}=\varepsilon_1$
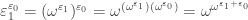
  7) $\varepsilon_1^{\varepsilon_0} = (\omega^{\varepsilon_1})^{\varepsilon_0}=\omega^{(\omega^{\varepsilon_1})}{^{(\omega^{\varepsilon_0})}}=\omega^{\omega^{\varepsilon_1+\varepsilon_0}}$
  8) $\varepsilon_1^{\varepsilon_1} = (\omega^{\varepsilon_1})^{\varepsilon_1}=\omega^{(\omega^{\varepsilon_1})}{^{(\omega^{\varepsilon_1})}}=\omega^{\omega^{\varepsilon_1.2}}$
  
  Hope that all renders properly!
  
  Reply
  - Rob Superty says:
    
    4 July, 2016 at 8:36 am
    
    Ah! A touch too late :)
    
    Reply
  - John Baez says:
    
    4 July, 2016 at 8:43 am
    
    It’s never too late! When two people independently get the same answer, it increases the spectators’ confidence that the answer is right.
    
    Reply
Marek14 says:

4 July, 2016 at 8:24 am

Now, you have written that ${\epsilon_1}$ is the limit of the sequence

$\epsilon_0 + 1, \; \omega^{\epsilon_0 + 1}, \; \omega^{\omega^{\epsilon_0 + 1}}, \; \omega^{\omega^{\omega^{\epsilon_0 + 1}}},\dots$

So, what is, say, limit of this similar sequence:

$\epsilon_0 + 2, \; \omega^{\epsilon_0 + 2}, \; \omega^{\omega^{\epsilon_0 + 2}}, \; \omega^{\omega^{\omega^{\epsilon_0 + 2}}},\dots$ ?

Should it be greater than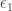 $\epsilon_1$ , but probably smaller than $\epsilon_2$ ?

Second question: all the limit ordinals constructed so far are supremas of some infinite sequences, i.e. sequences with $\omega$ members. Are there countable ordinals that require longer sequences? Or can all ordinals below $\omega_1$ (the first uncountable ordinal, which of course cannot be expressed in countable terms) be expressed using sequences with $\omega$ members?

Reply
- Rob Superty says:
  
  4 July, 2016 at 8:51 am
  
  Hi Marek – my instinct would be that the sequence you reference would still only indicate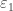 $\varepsilon_1$ , but I’ll leave it to the experts to explain/confirm. Interestingly, 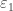$\varepsilon_1$ can also be represented by an infinite tower of $\varepsilon_0$ . One thing I find fascinating is the surreal number system, which gives meaning to forms like $\varepsilon_{-1}$ and $\varepsilon_{1/2}$ . But that’s a huge topic in itself! I’d recommend Gonshor’s Introduction to the Theory of Surreal Numbers if you’d like to learn more.
  
  Reply
  - Marek14 says:
    
    4 July, 2016 at 9:10 am
    
    Oh, I’m familiar with those. Some people admired actors or singers in their teens; my idol was Conway, ever since I found a copy of Winning Ways in a local university library.
    
    Reply
- John Baez says:
  
  4 July, 2016 at 8:52 am
  
  Marek14 wrote:
  
  So, what is, say, the limit of this similar sequence:
  
  $\epsilon_0 + 2, \; \omega^{\epsilon_0 + 2}, \; \omega^{\omega^{\epsilon_0 + 2}}, \; \omega^{\omega^{\omega^{\epsilon_0 + 2}}},\dots$ ?
  
  Should it be greater than $\epsilon_1$ , but probably smaller than $\epsilon_2$ ?
  
  This is a good puzzle. I’ll just give a small hint.
  
  Let’s call the limit of this sequence $x.$ It’s pretty easy to see that
  
  $x = \omega^x$
  
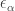  So, by definition, $x$ is an epsilon number. If it’s the $\alpha$ th epsilon number, we call it $\epsilon_\alpha$ .
  
  So, it can’t be greater than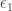 $\epsilon_1$ and smaller than 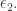$\epsilon_2.$ There are no epsilon numbers between these two!
  
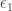  On the other hand, $x$ is certainly greater than or equal to $\epsilon_1$ , which is the limit of
  
  $\epsilon_0 + 1, \; \omega^{\epsilon_0 + 1}, \; \omega^{\omega^{\epsilon_0 + 1}}, \; \omega^{\omega^{\omega^{\epsilon_0 + 1}}},\dots$
  
  After all, each term in the sequence you gave is greater than or equal to the corresponding term in this sequence.
  
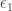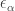  So, $x$ is either $\epsilon_1$ , $\epsilon_2$ , or $\epsilon_\alpha$ for some $\alpha > 2$ .
  
  At this point I will shut up and let others continue.
  
  Reply
- Royce Peng says:
  
  4 July, 2016 at 8:53 am
  
  If we call the first sequence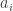 $a_i$ and the second sequence 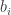$b_i$ , notice that
  
  $a_1 < b_1 < a_2 < b_2 < a_3 < b_3 \ldots$ .
  
  So it should be clear that any ordinal larger than all of the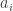 $a_i$ will also be larger than all of the 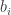$b_i$ and vice versa, so of course the smallest such ordinal will be the same for both.
  
  Remember that an ordinal $\alpha$ is countably infinite if and only if there is a bijection f from the natural numbers to $\alpha$ . So if $\alpha$ is limit, we can form a sequence of length $\omega$ by starting with f(0), then selecting the first f(n) that is greater than it, then the next greater ordinal, and so on. This is obviously a sequence of length $\omega$ , and it will have limit $\alpha$ , since for any ordinal $\beta < \alpha$ , we will at some point pass $\beta$ in the sequence, at which point we will either select $\beta$ , or pass it by because we have already exceeded it.
  
  Reply
bjonas says:

4 July, 2016 at 4:52 pm

Your description of the Veblen normal form is a bit confused, it mixes alpha and beta.

Reply
- John Baez says:
  
  5 July, 2016 at 2:51 am
  
  Thanks, I’ll check that out and fix if it needed.
  
  Reply
- John Baez says:
  
  5 July, 2016 at 2:58 am
  
  I don’t see a mistake here:
  
  Theorem. Any ordinal $\beta$ can be written uniquely as
  
  $\beta = \phi_{\gamma_1}(\alpha_1) + \dots + \phi_{\gamma_{k}}(\alpha_{k})$
  
  where $k$ is a natural number, each term is less than or equal to the previous one, and $\alpha_{i} < \phi_{\gamma_{i}}(\alpha_i)$ for all $i.$
  
  Reply
  - Anonymous says:
    
    6 July, 2016 at 2:43 am
    
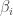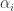    The paragraphs after that refer to $\beta_i$ as $\alpha_i$ (and to $\alpha$ as $\beta$ )
    
    Reply
    - John Baez says:
      
      6 July, 2016 at 5:22 am
      
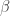      Got it! Thanks. Fixed.
      
      By the way, Wikipedia says that in Veblen normal form we have
      
      $\alpha_i < \phi_{\gamma_i}(\alpha_i)$
      
      but I’m afraid we might only have
      
      $\alpha_i \le \phi_{\gamma_i}(\alpha_i)$
      
      when $\beta$ reaches or exceeds the small Veblen ordinal, which is a fixed point of all the functions $\phi_\gamma.$
      
      What’s the Veblen normal form of the small Veblen ordinal? I feel I only understand Veblen normal form for ordinals below this.
    - Royce Peng says:
      
      6 July, 2016 at 7:07 am
      
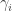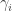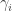      We can always have $\alpha_i < \varphi_{\gamma_i}(\alpha_i)$ , by choosing $\gamma_i$ to be as large as possible. (We can choose a maximal $\gamma_i$ since the set of possible values is closed; but if $\alpha_i = \varphi_{\gamma_i}(\alpha_i)$ then we can increase $\gamma_i$ by one.)
      
      The Veblen normal form for any strongly critical ordinal $\latex \alpha$ such as the Small Veblen Ordinal is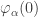 $\varphi_\alpha(0)$ .
    - John Baez says:
      
      6 July, 2016 at 8:53 am
      
      Thanks! Now I feel dumb, because I should have been able to figure that out. But that’s very helpful and reassuring.
Refurio Anachro says:

4 July, 2016 at 9:03 pm

Wow. You really made this one roll, John. I have to admit, I thought about collecting stuff for a book as well, but reading this post I might end up preferring to suggest yours. Fancy! And no, that wouldn’t stop me.

Reply
- John Baez says:
  
  5 July, 2016 at 3:06 am
  
  Thanks! It was your post on the Feferman–Schütte ordinal that revived my interest in explaining these ordinals:
  
  https://plus.google.com/+RefurioAnachro/posts/KNabqFVa8SM
  
  (It’s cool how a G+ post automatically shows up here; I’d never tried that trick before.)
  
  Reply
Royce Peng says:

5 July, 2016 at 5:48 am

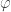Near the end you say that every ordinal less than the Feferman-Schutte ordinal can be expressed in terms of $1, +$ , and the $\varphi$ function. The 1 should be replaced by 0 I think.

Also, I think ordinal neophytes will be at a loss on how to get things like $\varepsilon_\omega$ and $\varphi_\omega(\alpha)$ ; perhaps you could add some detail there?

Reply
- John Baez says:
  
  5 July, 2016 at 8:29 am
  
  Royce wrote:
  
  The 1 should be replaced by 0 I think.
  
  You’re right!
  
  perhaps you could add some detail there?
  
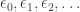
  Hmm, I don’t want to turn this road trip into a textbook… and the advantage of blog articles is that people can ask questions… but I’ll mention that $\epsilon_\omega$ is the first ordinal bigger than $\epsilon_0, \epsilon_1, \epsilon_2, \dots$
  
  Next time I’ll talk about some of this stuff a bit more formally.
  
  Reply
  - Marek14 says:
    
    5 July, 2016 at 9:57 am
    
    Well, maybe it would be easier to say that $\epsilon_\omega = \epsilon_0 + \epsilon_1 + \epsilon_2 + \dots$ ?
    
    Reply
    - Royce Peng says:
      
      5 July, 2016 at 10:05 am
      
      That might be more concise, but perhaps more confusing to the uninitiated. (I think it’s less clear that the ordinal defined by that expression is closed under omega exponentiation, for example.)
    - John Baez says:
      
      5 July, 2016 at 12:30 pm
      
      If I said
      
      $\epsilon_\omega = \epsilon_0 + \epsilon_1 + \epsilon_2 + \cdots$
      
      someone might point out that I haven’t defined an infinite sum of ordinals, or even pointed to a definition.
      
      Of course the definition of this infinite sum is that it’s the limit of
      
      $\epsilon_0, \; \epsilon_0 + \epsilon_1, \; \epsilon_0 + \epsilon_1 + \epsilon_2, \dots$
      
      but that seems more complicated than saying $\epsilon_\omega$ is the limit of
      
      $\epsilon_0, \; \epsilon_1, \; \epsilon_2, \dots$
Large Countable Ordinals (Part 3) | Azimuth says:

7 July, 2016 at 1:00 am

Last time we saw how to name a lot of countable ordinals using an idea developed by Veblen. In fact, all ordinals less than the ‘Feferman–Schütte ordinal’. This time I’ll explain Veblen’s idea more precisely and go even further, still using Veblen’s work.

Reply
Non-standard Models of Arithmetic 8 | Diagonal Argument says:

17 May, 2019 at 8:53 pm

Getting back to the Paris-Harrington theorem: the original proof used non-standard models of PA. (Kanamori and McAloon soon simplified it; the treatment in the recent book by Katz and Reimann is particularly easy to follow.) That’s the one I want to look at here.

But since you had such fun with ordinals here (and here and here), I better add that Ketonen and Solovay later gave a proof based on the ε₀ stuff and the hierarchy of fast-growing functions. (The variation due to Loebl and Nešetřil is nice and short.) We should talk about this sometime! I wish I understood all the connections better. (Stillwell’s Roads to Infinity offers a nice entry point, though he does like to gloss over details.)

Reply

You can use Markdown or HTML in your comments. You can also use LaTeX, like this: $latex E = m c^2 $. The word 'latex' comes right after the first dollar sign, with a space after it. Cancel reply

Enter your comment here...

Fill in your details below or click an icon to log in:

Email (required) (Address never made public)

Name (required)

Website

You are commenting using your WordPress.com account. ( Log Out / Change )

You are commenting using your Facebook account. ( Log Out / Change )

Cancel

Connecting to %s

This site uses Akismet to reduce spam. Learn how your comment data is processed.

	John Bonnett on Dividing a Square into 7 Simil…
	Ike Nassi on The Future of Physics
	Keith Harbaugh on The Future of Physics
	First Approximation on The Future of Physics
	Grandpa D on The Future of Physics
	Phillip Helbig on The Future of Physics
	Wyrd Smythe on The Future of Physics
	ken Abbott on The Future of Physics
	John Baez on Galois’ Fatal Duel
	Wolfgang on Galois’ Fatal Duel

Azimuth