Last time we saw why it’s devilishly hard to give names to large countable ordinals.
An obvious strategy is to make up a function from ordinals to ordinals that grows really fast, so that
is a lot bigger than the ordinal
indexing it. This is indeed a good idea. But something funny tends to happen! Eventually
catches up with
In other words, you eventually hit a solution of
This is called a fixed point of At this point, there’s no way to use
as a name for
unless you already have a name for
So, your scheme fizzles out!
For example, we started by looking at powers of the smallest infinite ordinal. But eventually we ran into ordinals
that obey
There’s an obvious work-around: we make up a new name for ordinals that obey
We call them epsilon numbers. In our usual nerdy way we start counting at zero, so we call the smallest solution of this equation and the next one
and so on.
But eventually we run into ordinals that are fixed points of the function
meaning that
There’s an obvious work-around: we make up a new name for ordinals that obey
But by now you can guess that this problem will keep happening, so we’d better get systematic about making up new names! We should let
and let be the
th fixed point of
Oswald Veblen, a mathematician at Princeton, came up with this idea around 1908, based on some thoughts of G. H. Hardy:
• Oswald Veblen, Continuous increasing functions of finite and transfinite ordinals, Trans. Amer. Math. Soc. 9 (1908), 280–292.
He figured out how to define even when the index
is infinite.
Last time we saw how to name a lot of countable ordinals using this idea: in fact, all ordinals less than the ‘Feferman–Schütte ordinal’. This time I want go further, still using Veblen’s work.
First, however, I feel an urge to explain things a bit more precisely.
Veblen’s fixed point theorem
There are three kinds of ordinals. The first is a successor ordinal, which is one more than some other ordinal. So, we say is a successor ordinal if
for some The second is 0, which is not a successor ordinal. And the third is a limit ordinal, which is neither 0 nor a successor ordinal. The smallest example is
Every limit ordinal is the ‘limit’ of ordinals less than it. What does that mean, exactly? Remember, each ordinal is a set: the set of all smaller ordinals. We can define the limit of a set of ordinals to be the union of that set. Alternatively, it’s the smallest ordinal that’s greater than or equal to every ordinal in that set.
Now for Veblen’s key idea:
Veblen’s Fixed Point Theorem. Suppose a function from ordinals to ordinals is:
• strictly increasing: if then
and
• continuous: if is a limit ordinal,
is the limit of the ordinals
where
Then must have a fixed point.
Why? For starters, we always have this fact:
After all, if this weren’t true, there’d be a smallest with the property that
since every nonempty set of ordinals has a smallest element. But since
is strictly increasing,
so would be an even smaller ordinal with this property. Contradiction!
Using this fact repeatedly, we get
Let be the limit of the ordinals
Then by continuity, is the limit of the sequence
So equals
Voilà! A fixed point!
This construction gives the smallest fixed point of . There are infinitely many more, since we can start not with
but with
and repeat the same argument, etc. Indeed if we try to list these fixed points, we find there is one for each ordinal.
So, we can make up a new function that lists these fixed points. Just to be cute, people call this the derivative of so that
is the
th fixed point of
Beware: while the derivative of a polynomial grows more slowly than the original polynomial, the derivative of a continuous increasing function
from ordinals to ordinals generally grows more quickly than
It doesn’t really act like a derivative; people just call it that.
Veblen proved another nice theorem:
Theorem. If is a continuous and strictly increasing function from ordinals to ordinals, so is
So, we can take the derivative repeatedly! This is the key to the Veblen hierarchy.
If you want to read more about this, it helps to know that a function from ordinals to ordinals that’s continuous and strictly increasing is called normal. ‘Normal’ is an adjective that mathematicians use when they haven’t had enough coffee in the morning and aren’t feeling creative—it means a thousand different things. In this case, a better term would be ‘differentiable’.
Armed with that buzzword, you can try this:
• Wikipedia, Fixed-point lemma for normal functions.
Okay, enough theory. On to larger ordinals!
The Feferman–Schütte barrier
First let’s summarize how far we got last time, and why we got stuck. We inductively defined the th ordinal of the
th kind by:
and
meaning that is the
th fixed point of
This handles the cases where is zero or a successor ordinal. When
is a limit ordinal we let
be the
th ordinal that’s a fixed point of all the functions
for
Last time I explained how these functions give a nice notation for ordinals less than the Feferman–Schütte ordinal, which is also called
This ordinal is the smallest solution of
So it’s a fixed point, but of a new kind, because now the appears as a subscript of the
function.
We can get our hands on the Feferman–Schütte ordinal by taking the limit of the ordinals
(If you’re wondering why we use the number 0 here, instead of some other ordinal, I believe the answer is: it doesn’t really matter, we would get the same result if we used any ordinal less than the Feferman–Schütte ordinal.)
The ‘Feferman–Schütte barrier’ is the combination of these two facts:
• On the one hand, every ordinal less than
can be written as a finite sum of guys
where
and
are even smaller than
Using this fact repeatedly, we can get a finite expression for any ordinal less than the Feferman–Schütte ordinal in terms of the
function, addition, and the ordinal 0.
• On the other hand, if and
are less than
then
is less than
So we can’t use the
function to name the Feferman–Schütte ordinal in terms of smaller ordinals.
But now let’s break the Feferman–Schütte barrier and reach some bigger countable ordinas!
The Γ function
The function is strictly increasing and continuous as a function of
So, using Veblen’s theorems, we can define
to be the
th solution of
We can then define a bunch of enormous countable ordinals:
and still bigger ones:
and even bigger ones:
and even bigger ones:
But since is just
we can reach much bigger countable ordinals with the help of the
function:
and we can do vastly better using the function itself:
The limit of all these is the smallest solution of
As usual, this ordinal is still countable, but there’s no way to express it in terms of the function and smaller ordinals. So we are stuck again.
In short: we got past the Feferman–Schütte barrier by introducing a name for the th solution of
We called it
This made us happy for about two minutes…
…. but then we ran into another barrier of the same kind. ![]()
So what we really need is a more general notation: one that gets us over not just this particular bump in the road, but all bumps of this kind! We don’t want to keep randomly choosing goofy new letters like We need something systematic.
The multi-variable Veblen hierarchy
We were actually doing pretty well with the function. It was nice and systematic. It just wasn’t powerful enough. But if you’re trying to keep track of how far you’re driving on a really long trip, you want an odometer with more digits. So, let’s try that.
In other words, let’s generalize the function to allow more subscripts. Let’s rename
and call it
. The fact that we’re using two subscripts says that we’re going beyond the old
functions with just one subscript. The subscripts 1 and 0 should remind you of what happens when you drive more than 9 miles: if your odometer has two digits, it’ll say you’re on mile 10.
Now we proceed as before: we make up new functions, each of which enumerates the fixed points of the previous one:
and so on. In general, we let
and when is a limit ordinal, we let
Are you confused?
How could you possibly be confused???
Okay, maybe an example will help. In the last section, our notation fizzled out when we took the limit of these ordinals:
The limit of these is the smallest solution of But now we’re writing
so this limit is the smallest fixed point of
So, it’s
We can now ride happily into the sunset, defining for all ordinals
Of course, this will never give us a notation for ordinals with
But we don’t let that stop us! This is where the new extra subscript really comes in handy. We now define to be the
th solution of
Then we drive on as before. We let
and when is a limit ordinal, we say
I hope you get the idea. Keep doing this!
We can inductively define for all
and
Of course, these functions will never give a notation for solutions of
To describe these, we need a function with one more subscript! So let be the
th solution of
We can then proceed on and on and on, adding extra subscripts as needed.
This is called the multi-variable Veblen hierarchy.
Examples
To help you understand the multi-variable Veblen hierarchy, I’ll use it to describe lots of ordinals. Some are old friends. Starting with finite ones, we have:
•
•
and so on, so we don’t need separate names for natural numbers… but I’ll use them just to save space.
•
•
and so on, so we don’t need separate names for and its powers, but I’ll use them just to save space.
•
•
•
•
•
•
•
where I should remind you that is a name for the
th solution of
•
•
•
• is the limit of
• is called the Ackermann ordinal.
Apparently Wilhelm Ackermann, the logician who invented a very fast-growing function called Ackermann’s function, had a system for naming ordinals that fizzled out at this ordinal.
The small Veblen ordinal
There are obviously lots more ordinals that can be described using the multi-variable Veblen hierarchy, but I don’t have anything interesting to say about them. And you’re probably more interested in this question: what’s next?
The limit of these ordinals
is called the small Veblen ordinal. Yet again, it’s a countable ordinal. It’s the smallest ordinal that cannot be named in terms of smaller ordinals using the multi-variable Veblen hierarchy…. at least, not the version I described. And here’s a nice fact:
Theorem. Every ordinal less than the small Veblen ordinal can be written as a finite expression in terms of the multi-variable
function, addition, and 0.
For example,
is equal to
On the one hand, this notation is quite tiresome to read. On the other hand, it’s amazing that it gets us so far!
Furthermore, if you stare at expressions like the above one for a while, and think about them abstractly, they should start looking like trees. So you should find it easy to believe that ordinals less than the small Veblen ordinal correspond to trees, perhaps labelled in some way.
Indeed, this paper describes a correspondence of this sort:
• Herman Ruge Jervell, Finite trees as ordinals, in New Computational Paradigms, Lecture Notes in Computer Science 3526, Springer, Berlin, 2005, pp. 211–220.
However, I don’t think his idea is quite same as what you’d come up with by staring at expressions like
Beyond the small Veblen ordinal
We’re not quite done yet. The modifier ‘small’ in the term ‘small Veblen ordinal’ should make you suspect that there’s more in Veblen’s paper. And indeed there is!
Veblen actually extended his multi-variable function to the case where there are infinitely many variables. He requires that all but finitely many of these variables equal zero, to keep things under control. Using this, one can set up a notation for even bigger countable ordinals! This notation works for all ordinals less than the large Veblen ordinal.
We don’t need to stop here. The large Veblen ordinal is just the first of a new series of even larger countable ordinals!
These can again be defined as fixed points. Yes: it’s déjà vu all over again. But around here, people usually switch to a new method for naming these fixed points, called ‘ordinal collapsing functions’. One interesting thing about this notation is that it makes use of uncountable ordinal. The first uncountable ordinal is called and it dwarfs all those we’ve seen here.
We can use the ordinal collapsing function to name many of our favorite countable ordinals, and more:
• is
the smallest solution of
• is
the Feferman–Schütte ordinal.
• is the Ackermann ordinal.
• is the small Veblen ordinal.
• is the large Veblen ordinal.
• is called the Bachmann–Howard ordinal. This is the limit of the ordinals
I won’t explain this now. Maybe later! But not tonight. As Bilbo Baggins said:
The Road goes ever on and on
Out from the door where it began.
Now far ahead the Road has gone,
Let others follow it who can!
Let them a journey new begin,
But I at last with weary feet
Will turn towards the lighted inn,
My evening-rest and sleep to meet.
For more
But perhaps you’re impatient and want to begin a new journey now!
The people who study notations for very large countable ordinals tend to work on proof theory, because these ordinals have nice applications to that branch of logic. For example, Peano arithmetic is powerful enough to work with ordinals up to but not including , so we call
the proof-theoretic ordinal of Peano arithmetic. Stronger axiom systems have bigger proof-theoretic ordinals.
Unfortunately this makes it a bit hard to learn about large countable ordinals without learning, or at least bumping into, a lot of proof theory. And this subject, while interesting in principle, is quite tough. So it’s hard to find a readable introduction to large countable ordinals.
The bibliography of the Wikipedia article on large countable ordinals gives this half-hearted recommendation:
Wolfram Pohlers, Proof theory, Springer 1989 ISBN 0-387-51842-8 (for Veblen hierarchy and some impredicative ordinals). This is probably the most readable book on large countable ordinals (which is not saying much).
Unfortunately, Pohlers does not seem to give a detailed account of ordinal collapsing functions. If you want to read something fun that goes further than my posts so far, try this:
• Hilbert Levitz, Transfinite ordinals and their notations: for the uninitiated.
(Anyone whose first name is Hilbert must be born to do logic!)
This is both systematic and clear:
• Wikipedia, Ordinal collapsing functions.
And if you want to explore countable ordinals using a computer program, try this:
• Paul Budnik, Ordinal calculator and research tool.
Among other things, this calculator can add, multiply and exponentiate ordinals described using the multi-variable Veblen hierarchy—even the version with infinitely many variables!

Some more puzzles. I don’t know the answers to all of these. In all cases there will be more than one correct way to write the answer, so your goal can be either to find the simplest, or to use one of the ‘normal forms’ I’ve described. Depending on what you’re trying to do, you may decide that the question is already the best answer. Please say what you’re trying to do!
Puzzle 1. What is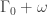 ?
?
Puzzle 2. What is ?
?
Puzzle 3. What is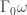 ?
?
Puzzle 4. What is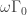 ?
?
Puzzle 5. What is ?
?
Puzzle 6. What is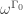 ?
?
Puzzle 7. What is ?
?
Puzzle 8. What is ?
?
Puzzle 9. What is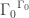 ?
?
Puzzle 10. What is ?
?
Puzzle 11. What is ?
?
Puzzle 12. What is ?
?
For the next ones, let be the small Veblen ordinal.
be the small Veblen ordinal.
Puzzle 13. What is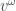 ?
?
Puzzle 14. What is ?
?
Well, for 2, 4, 6, and 8,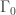 is so big it “swallows” the other term, so all of these will be
is so big it “swallows” the other term, so all of these will be 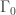 . Similarly for 11 and 14, since
. Similarly for 11 and 14, since  will be a fixed point of
will be a fixed point of 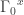 and small Veblen ordinal will be definitely a fixed point of
and small Veblen ordinal will be definitely a fixed point of 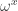 .
.
Puzzle 1 is a sum — we can’t do much about that,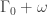 is probably the best we can do.
is probably the best we can do.
Puzzle 3: Since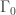 must be a fixed point of
must be a fixed point of 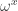 , we can rewrite the puzzle as
, we can rewrite the puzzle as 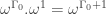 .
.
Similar logic says that Puzzle 5 is . And in fact, as long as we have just a simple exponential term…
. And in fact, as long as we have just a simple exponential term…
Puzzle 7: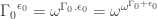
Puzzle 9: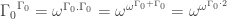
Puzzle 10: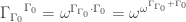
Puzzle 12:
And even Puzzle 13 is nothing more than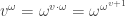 .
.
Basically: for ordinals beyond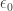 , these exponentiations are trivial.
, these exponentiations are trivial.
I really wish there was an edit tool, or at least a preview mode…
Me too!
The definitions and
and  when
when  is a limit ordinal are incorrect; for example,
is a limit ordinal are incorrect; for example,  for all
for all  . The description that you give right after (that
. The description that you give right after (that  is the
is the  th ordinal that is a fixed point of
th ordinal that is a fixed point of 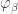 for all
for all  ) is probably the simplest way to define
) is probably the simplest way to define  .
.
Oh, darn, I hoped that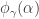 defined the correct way, would wind up being continuous in the variable
defined the correct way, would wind up being continuous in the variable  . But it’s just continuous in the variable
. But it’s just continuous in the variable 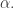
Thanks! I’ll fix that.
Various issues connected to this made me shy away from giving a precise recursive definition of the multi-variable Veblen function. I found the definition here incomprehensible: in particular, something about the location of all those zeroes in the third clause confuses me. If I patiently work out some examples maybe it will make sense. And if I’d carefully read that passage I would have seen
Were you involved in writing this Wikipedia article? It’s basically very good.
Now that I think about it, you can have continuity in the variable , by defining
, by defining  just like you said. Then we will have
just like you said. Then we will have  , so the new notation will reach just as far as the old one. Unfortunately, this makes other things less nice, for example
, so the new notation will reach just as far as the old one. Unfortunately, this makes other things less nice, for example  will not normal, and neither will
will not normal, and neither will  , so for example we can have things like
, so for example we can have things like  . But it’s an interesting alternative!
. But it’s an interesting alternative!
In the third clause of the multi-variable function definition, the number of zeroes is the same, but shifted over one to the right; this is just a consequence of the fact that the enumerating variable is the rightmost one, while the variable that we are taking fixed points of is the one right after the last nonzero variable. So for example (using to denote the last nonzero variable)
to denote the last nonzero variable)
and so on.
I wasn't involved with the Wikipedia article; for some reason I haven't gotten around to editing Wikipedia, although I use it very often. It looks like Gro-Tsen was heavily involved with the countable ordinal articles, though.
I think I have to plead guilty for writing this “incomprehensible” definition, and I think I remember being rather unhappy about it and hoping to find a better formulation later. Apparently, three years later, this has not happened. And the definition for transfinitely many variables is, arguably, even worse: I even wrote in the edit comment that I wasn’t able to word it in a simple way.
On the other hand, I also wrote the “ordinal collapsing function” Wikipedia article, which many people seem to have found useful. So all hope is not lost for my expository skills. ☺
Your expository skills are very good! The one issue I have with the article is the uncertain way you describe fundamental sequences for when
when  has uncountable cofinality. I think the “nice” way to handle this is to define fundamental sequences for ordinals of uncountable cofinality as well, and use those to define
has uncountable cofinality. I think the “nice” way to handle this is to define fundamental sequences for ordinals of uncountable cofinality as well, and use those to define  when
when  has uncountable cofinality. On the other hand, uncountable fundamental sequences may be confusing for the audience, so I’m not sure which approach is better.
has uncountable cofinality. On the other hand, uncountable fundamental sequences may be confusing for the audience, so I’m not sure which approach is better.
Gro-Tsen: your writeup of ordinal collapsing functions is so good that I barely see the point in blogging about this concept! It has a reputation for being advanced and difficult, but you have made it clear, attractive and exciting. This is Wikipedia at its best.
I still hope to blog about ordinal collapsing functions someday, just to bring greater attention to this concept. But right now, my blog article would be just a portion of that Wikipedia article, expanded with extra fluff.
Right now the only way I see to comprehend the recursive definition of the multi-variable Veblen function is to give lots of examples, as I started to do in this blog article. I may take Royce’s examples above and copy them into Wikipedia. Someday I may rewrite the explanation in this blog article and try to improve it. (I keep dreaming of a book about this stuff….)
I think the “odometer” analogy may be useful. If you try to explain how to add one to a number written in base 10, it sounds fairly complicated, due to the numbers that can end in arbitrarily long strings of 9’s. And yet most children are able to learn it… though some wind up hating math.
Since John is giving references, I’d like to self-promote my own series of articles on ordinal notations:
http://googology.wikia.com/wiki/User_blog:Deedlit11/Ordinal_Notations_I:_Up_to_the_Schutte_Klammersymbolen
http://googology.wikia.com/wiki/User_blog:Deedlit11/Ordinal_notations_II:_Up_to_the_Bachmann-Howard_ordinal
http://googology.wikia.com/wiki/User_blog:Deedlit11/Ordinal_Notations_III:_Collapsing_Higher_Cardinalities
http://googology.wikia.com/wiki/User_blog:Deedlit11/Ordinal_Notations_IV:_Up_to_a_weakly_inaccessible_cardinal
http://googology.wikia.com/wiki/User_blog:Deedlit11/Ordinal_Notations_V:_Up_to_a_weakly_Mahlo_cardinal
http://googology.wikia.com/wiki/User_blog:Deedlit11/Ordinal_Notations_VI:_Up_to_a_weakly_compact_cardinal
The first article describes ordinals up to the Large Veblen Ordinal, the second goes up to the Bachmann-Howard Ordinal, and the remaining four go far beyond. Unlike John’s articles I probably fail to avoid the trap of “reading like a textbook”, but I tried to explain the notations as well as I can. Anyway, I’d appreciate any comments, even critical ones!
For some other introductions to large countable ordinals, we have
which is actually an introduction to “ridiculously huge (finite) numbers”, but morphs into talking about transfinite ordinals, since in the later parts he mainly uses the fast-growing hierarchy to create large finite numbers. I believe the ordinals start in part 5. It’s a very gentle introduction, only going up to the Feferman-Schutte ordinal, but he also talks about related topics like Goodstein sequences, Friedman’s long finite sequences and the TREE function.
David Metzler also has a playlist for ordinal numbers specifically:
Mark Giroux also has a Youtube series on large countable ordinals:
The presentation isn’t quite as nice as Metzler’s, but he goes considerably farther, beyond the Bachmann-Howard ordinal.
Here is a written description of some ordinal notations:
http://quibb.blogspot.com/p/infinity-series-portal.html
although the description of ordinal collapsing functions of higher cardinalities isn’t quite right.
Thanks for all these references! I’ve already made use of some material on Googology, which you probably had a hand in. But I don’t think I’ve seen your own personal explanations. I’m eager to read them!
Mind you, it’s not like I’m opposed to textbooks. There really needs to be a good textbook on this material. The business of writing an ‘entertaining’ account should come later: then it can refer to the textbook. But apparently no such textbook exists.
What I’d really like to do is write a paper that’s entertaining and yet has enough detail to be fully self-contained. This can be hard: to be entertaining you have to omit some details, but to be self-contained you have to put them in.
My strategy for dealing with this is to use the “spiral approach”: first giving a rough account and then refining it a bit at a time.
This makes for a really absorbing story when it’s done right, but it can be frustrating for people who want full precision right away—e.g. trained mathematicians, not normal human beings.
One solution to this problem is to have links to something like a glossary, which defines everything precisely in a terse way. On my blog I try to give Wikipedia links to accomplish that task… but I dream of writing self-contained accounts that have those glossaries built in.
If I ever get more serious about writing about large ordinals, I’ll definitely ask you for help. I’d love to write a book on this stuff. Unfortunately I’d love to do lots of things, so most of my projects will remain half-assed and incomplete. But I’m planning to take some of my favorite expository writing, polish it up a little but not so much that the task becomes huge, and put it on the arXiv.
@John Baez
You are definitely nailing the entertainment part! I feel like there should be an entire wiki-like portal which, from the get-go, attempts to explain this stuff that way, including such a glossary function and everything. It would be amazing!
I hesitate to ask, but what did you think of my articles? Comprehensible, or not?
I think they’re an invaluable resource. I sort of understand them. I bet I could really understand them if I really put my mind to it. I bet I actually will someday! But I’m getting busy on another project, so it may take a while.
I find that I most enjoy explanations that use lots of well-crafted English prose. Many mathematicians, and proof theorists in particular, seem to be averse to saying what they’re actually thinking. You have to stare at their formulas and guess what they’re up to do—it’s a bit like that game of pantomime where someone mutely gestures in complicated ways, you rack your brains, and gradually it dawns on you: they’re trying to indicate a bicycle. Of course as a professional mathematician I’m used to this, but it’s tiring.
So, for example, if Gro-Tsen had only written:
I would not be complimenting him on his explanation of ordinal collapsing functions. But he prefaced this by describing the same idea in English:
and then he came out and explained the actual point:
Seeing the same idea explained in three different ways makes it possible for me to understand it very quickly, almost ‘instantly’. I don’t have the feeling that I’m decoding hieroglyphics: instead, my eye flickers over the text and the idea shoots straight into my brain.
The third, supposedly ‘obscure’ description is the clearest to me—but it’s important that I can go back to the other two and see that yes, this is how you formalize that idea. And other readers, more fond of formalism, will be greatly reassured by seeing all that set-builder notation. Different people learn in different ways.
Here’s a question, Royce. When you start using large cardinals like weakly inaccessible cardinals, Mahlo cardinals etc. to construct notations for countable ordinals, do you need to add large cardinal axioms to ZFC to prove that the resulting countable ordinals actually exist?
On the one hand it seems plausible, since you’re acting like these large cardinals exist.
On the other hand I sometimes get the feeling that the use of uncountable cardinals to create notations for countable ordinals is just a ‘convenient notational trick’. Maybe you don’t really need those cardinals, maybe you just need some symbols that follow certain rules.
I’m assuming all the countable ordinals you’re getting notations for are computable. Is that right?
It would be somewhat irksome if the structure of computable ordinals depended on large cardinal axioms. But I guess I should not be surprised: large cardinals have a nasty way of reaching down from the sky and affecting ordinary mathematics.
This reminds me of Yudkowsky’s winning solution to the xkcd contest for naming the largest computable natural number. He won it using the large cardinal axiom I0. Nobody knows if this axiom is relatively consistent with ZFC. If it’s not, I believe something bad happens to his ‘huge computable natural number’. (I can’t figure out what: maybe it doesn’t exist, or it becomes very small….)
So I’ll ask: what happens to those large countable ordinals you’re talking about, if the large cardinals you’re using to notate them turn out to be inconsistent with ZFC?
Hmm, this is somewhat tricky. It certainly seems to me that all these uncountable cardinals could be replaced by any set of ordinals, provided that the ordinals are “far enough apart”. So for example, just needs to be bigger than those ordinals which we currently identify as the countable ordinals (which of course is a set that keeps getting bigger as we keep extending the notation),
just needs to be bigger than those ordinals which we currently identify as the countable ordinals (which of course is a set that keeps getting bigger as we keep extending the notation),  just needs to be bigger than any ordinal that we are currently identifying as having cardinality
just needs to be bigger than any ordinal that we are currently identifying as having cardinality  , and so on. Now, those comparison rules get more and more complicated as we go to stronger and stronger notations, but it will still be a recursive relation, so we do indeed get the notation for a recursive ordinal – assuming the existence of those large cardinals.
, and so on. Now, those comparison rules get more and more complicated as we go to stronger and stronger notations, but it will still be a recursive relation, so we do indeed get the notation for a recursive ordinal – assuming the existence of those large cardinals.
Without the large cardinals, we can still define those comparison rules, but then we don’t have the background theory to easily prove that we get ordinals in the end. So, we still need to prove that the relation is a well-ordering. Unfortunately, this seems like a difficult task indeed.
For example, Taranovsky (http://web.mit.edu/dmytro/www/other/OrdinalNotation.htm) and Hyp Cos (https://stepstowardinfinity.wordpress.com/array/) define very strong notations (going beyond the weakly compact notation I described in my last blog post) without using large cardinals: Taranovsky defines a (relatively simple) comparison relation for his notation, whereas Hyp Cos defines the “limit ordinals” of his notation as the limit of other notations. (so basically he defines fundamental sequences.) The major open problem for both is proving that they are well-ordered.
A possible solution: Use recursive analogs of large cardinals! So instead of weakly inaccessible cardinals use recursively inaccessible ordinals, instead of weakly Mahlo cardinals use recursively Mahlo ordinals, and instead of weakly compact cardinals use -reflecting ordinals. I think this should solve the problem of defining the notation and at least knowing that it is well-ordered; the problem, according to Rathjen, is that the things you need to prove about the notation for their use in ordinal analysis become much harder. Rathjen talks about this in:
-reflecting ordinals. I think this should solve the problem of defining the notation and at least knowing that it is well-ordered; the problem, according to Rathjen, is that the things you need to prove about the notation for their use in ordinal analysis become much harder. Rathjen talks about this in:
Click to access WELL.pdf
I suspect that Taranovsky’s notations do not live up to their claims, although I asked the question on MathOverflow and nobody was willing to come forward and take a stand. More specifically, I think Taranovsky missed the fact (which is what makes ordinal analysis very delicate beyond Π₃-reflection) that to deal with Π₄-reflection we need to account for those ordinals which are Π₂-reflecting on a set of Π₃-reflecting ordinals, which means we need to go beyond collapsing functions and talk of collapsing hierarchies, and the technical difficulties are colossal.
As far as I was able to tell, the largest constructive countable ordinals to have been described in the mainstream mathematical literature is in Jan-Carl Stegert’s 2010 thesis, “Ordinal Proof Theory of Kripke-Platek Set Theory Augmented by Strong Reflection Principles” (he’s a student of Wolfram Pohlers’s, but no longer doing mathematics), building on ideas introduced by Rathjen (“An Ordinal Analysis of Stability“) but which contained technical errors. The description of the ordinal notation is impressively complex. Stegert deals essentially with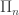 -reflection and a transfinite generalization thereof; this is still below
-reflection and a transfinite generalization thereof; this is still below  -comprehension. The case of
-comprehension. The case of  -reflection had been dealt (along different lines) in Christopher Duchhardt’s thesis (also a student of Pohlers’s).
-reflection had been dealt (along different lines) in Christopher Duchhardt’s thesis (also a student of Pohlers’s).
Yes, I too am suspicious of Taranovsky’s conjectures, as they seem quite extravangant. However, my analysis agreed with his claim that -reflection is reached quite early, even in the second level of his main notation. So it does appear to be quite a strong notation, at least at my “amateur” level.
-reflection is reached quite early, even in the second level of his main notation. So it does appear to be quite a strong notation, at least at my “amateur” level.
Concerning the mathematical literature, Rathjen has written a three part series of papers on the ordinal analysis of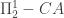 . The first paper is the one that you linked on the ordinal analysis of stability, which is as far as Stegert studied; however, Stegert found technical errors as you mention. The second is An Ordinal Analysis of Parameter Free Pi-1-2-Comprehension, which is gives an ordinal notation for the “parameter free” version of
. The first paper is the one that you linked on the ordinal analysis of stability, which is as far as Stegert studied; however, Stegert found technical errors as you mention. The second is An Ordinal Analysis of Parameter Free Pi-1-2-Comprehension, which is gives an ordinal notation for the “parameter free” version of 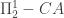 just as it says. I don’t know if the technical errors in the first paper migrate up to this one, or if the potential errors cause the ordinal notation to fail, but if not, this would seem to be the strongest published ordinal notation that I am aware of. Note that the definition of his collapsing function runs over 30 pages! The third paper is an analysis of full
just as it says. I don’t know if the technical errors in the first paper migrate up to this one, or if the potential errors cause the ordinal notation to fail, but if not, this would seem to be the strongest published ordinal notation that I am aware of. Note that the definition of his collapsing function runs over 30 pages! The third paper is an analysis of full 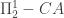 , but unfortunately this was never published; perhaps the technical difficulties became too much for any referee to verify.
, but unfortunately this was never published; perhaps the technical difficulties became too much for any referee to verify.
A researcher in the same area is Toshiyasu Arai, who also claimed to achieve an ordinal analysis of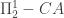 , but this is also apparently unpublished. I don’t know what the strongest ordinal notation is that he published; on the arXiv he has a paper on
, but this is also apparently unpublished. I don’t know what the strongest ordinal notation is that he published; on the arXiv he has a paper on 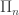 reflection, where he describes a ordinal notation initially defined elsewhere. Unlike Rathjen and Stegert, he uses a souped up version of Takeuti’s ordinal diagrams; although I understand Takeuti’s od’s, I can’t make sense of what’s going on here. At least the definition is far shorter than Rathjen’s.
reflection, where he describes a ordinal notation initially defined elsewhere. Unlike Rathjen and Stegert, he uses a souped up version of Takeuti’s ordinal diagrams; although I understand Takeuti’s od’s, I can’t make sense of what’s going on here. At least the definition is far shorter than Rathjen’s.
Gro-Tsen, can you make heads or tails of any of the ordinal notations of Rathjen/Arai/Stegert/Duchhardt? I still hold on to the fleeting hope that someone will explain it to me well enough for me to have at least some idea of what is going on. Duchhardt’s ordinal notation avoids the reflection instances / reflection configurations/ projection configurations of Rathjen and Stegert, so I understand every little bit of it, but I don’t understand why he defines it as he does or how it actually works.
Another strong published notation, which is actually my favorite ordinal notation, is patterns of resemblance; they were defined by Timothy Carlson way back in 1997 but they haven’t received a lot of attention. Carlson’s main introductory papers on first order patterns and second order patterns are a fun read. But I recommend anyone interested start with Samuel Alexander’s elementary introduction here. First order patterns reach , or the proof theoretic ordinal of
, or the proof theoretic ordinal of 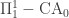 ; Carlson conjectures that the full system reaches
; Carlson conjectures that the full system reaches 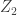 ! So perhaps second order patterns could reach
! So perhaps second order patterns could reach  ? No one knows yet. But patterns of resemblance could potentially be the strongest known notation.
? No one knows yet. But patterns of resemblance could potentially be the strongest known notation.
So that is the state of the art as far as I know; but the strongest notations I think I can understand are the notations of Taranosky and Hyp Cos, and to a lesser extent second order arithmetic patterns of resemblance.
(Replying to Royce Peng’s comment on 9 July, 2016 at 1:09 am)
First, I should note that I’m also an amateur (I’m an algebraic geometer). I was considering implementing some of these ordinal notation systems (perhaps add them to Sage as a data type), but the one in Stegert’s thesis is so complex that I gave up before I even started. I did manage to get to the point where it made at least some sort of sense (at least the one in part I, i.e., for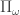 -reflection), not so much that I’d be able to explain it, but at least enough to wrap my mind around the fact that the complexity is not gratuitous. It helps a lot that between parts I and II he gives simplified versions of the system with increasing complexity: I remember going through exercises of trying to convert ordinal notations from Rathjen’s Proof Theory of Reflection to get a feel of how it works. (Interesting exercises involve writing notations for ordinals like “the first fixed point of
-reflection), not so much that I’d be able to explain it, but at least enough to wrap my mind around the fact that the complexity is not gratuitous. It helps a lot that between parts I and II he gives simplified versions of the system with increasing complexity: I remember going through exercises of trying to convert ordinal notations from Rathjen’s Proof Theory of Reflection to get a feel of how it works. (Interesting exercises involve writing notations for ordinals like “the first fixed point of 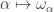 ” or “the first such fixed point above the first limit of inaccessible cardinals”, and similar.)
” or “the first such fixed point above the first limit of inaccessible cardinals”, and similar.)
I also have no idea of what happened with Rathjen’s papers. The footnote 4 on page 4 of Stegert’s thesis seems to say that the two first papers (“An ordinal analysis of stability” and “An ordinal analysis of parameter-free -comprehension”) both have technical errors, and the promised third does not seem to exist even as a preprint, so I had gathered that the author gave up on achieving full
-comprehension”) both have technical errors, and the promised third does not seem to exist even as a preprint, so I had gathered that the author gave up on achieving full  -comprehension, but I have no special knowledge here.
-comprehension, but I have no special knowledge here.
Thanks for the other references. I hadn’t heard about Carlson’s “patterns”, but I’ll definitely try to understand how they work. As for Arai’s ordinal diagrams, I must say I find their definition even more unreadable than that of Stegert’s collapsing hierarchies, but maybe it’s a matter of taste.
It would be great to see an article or post describing what little you do know about Stegert’s notation, but I certainly understand if you can’t do it. I’m currently trying to decipher the smaller ordinal notations in his Review section, but I’m not having much success since I can’t make heads or tails of his reflection instances/configurations.
I did once write to Rathjen and asked him about his third paper. He replied that it exists, but didn’t go into further detail. I suppose there is again the question of whether the technical errors that Stegert discovered invalidates this ordinal notation as well.
I do think patterns of resemblance would be a great notation to make a computer implementation of (probably only up to second order for now). But, I’m getting ahead of things.
If ZFC+I0 is unsound for Pi_1 statements, it might prove that a particular nonhalting machine halts, which would result in Yudkowsky’s algorithm running a nonhalting machine forever. If ZFC+I0 is inconsistent then it will prove all nonhalting machines halt, so Yudkowsky’s algorithm will definitely run forever.
Thanks!
I think there should be a contest to name the largest natural number by describing an algorithm to compute it which is provably guaranteed to termininate if ZFC is consistent. Or maybe just PA, or even some weaker system of arithmetic. We can have different contests for different axiom systems. But leaving the axioms open seems to reduce the challenge to finding the most powerful large cardinal axiom that 9 out of 10 set theorists suspect is consistent.
This new challenge has some difficulties. For example, I believe that Yudkowsky’s algorithm halts (since I believe ZFC+I0 is 1-consistent), so I believe that one can prove in ZFC that Yudkowsky’s algorithm halts, by just “following the procedure to completion”.
If we wish to stay within the spirit of the category, we could for instance just replace ZFC+I0 with ZFC. Now the obvious proof that this halts requires ZFC + “ZFC is 1-consistent”, not ZFC + “ZFC is consistent”, but this brings up another difficulty; if something is provable in ZFC, it is provable in a weaker theory than ZFC (call it T) such that ZFC proves the 1-consistency of T. (Or, at least I’m pretty sure that this is true.)
For example, suppose we submit Hydra^googol(googol) in the PA category (see http://googology.wikia.com/wiki/Kirby-Paris_hydra). Now, PA does not prove that arbitrary hydras reduce to zero in finite time. But, the weaker theory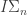 proves that hydras of height n or less always reduce to zero, so Hydra(googol) halts has a clear proof in
proves that hydras of height n or less always reduce to zero, so Hydra(googol) halts has a clear proof in  , and Hydra^2(googol) halts has a clear proof in
, and Hydra^2(googol) halts has a clear proof in 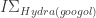 and so on. So if you have a function “just beyond” theory T, you can argue your way around it.
and so on. So if you have a function “just beyond” theory T, you can argue your way around it.
Royce wrote:
Heh. Clever. I distinguish between 1) believing that I could prove something if I carried out an incomprehensibly lengthy procedure and 2) actually exhibiting a proof. There are many things I believe I could prove, but I don’t say I’ve proved them until I have.
Anyway, this is fertile ground for argument. Clearly people who are more willing to believe things will be better able to believe they’ve named larger numbers. But I am not dogmatic: I’m willing to entertain many different contests, with different rules for what counts as success.
But I am not dogmatic: I’m willing to entertain many different contests, with different rules for what counts as success.
A rule that I would like would be to disallow entries that “busy beaver” their way out of a strong theory or strong language, like Yudkowsy does for ZFC+I0 and Loader does for the Calculus of Constructions in the Bignum Bakeoff. So basically we would be trying to find the strongest notation using explicit recursion; that’s where the fun is! (Unless of course someone finds another powerful paradigm, which would also be interesting.)
The large cardinals are definitely not necessary to define the notations (after all, the notations are ultimately character strings handled by a Turing machine). They are prima facie required to show that the notations are indeed ordinal notations (i.e., that they are well-founded). But as Royce Peng points out, it should be possible to prove the same thing using “recursively large” ordinals (recursively inaccessible, recursively Mahlo, etc.) ordinals instead, and ZFC proves their existence. In fact, that is the “correct” thing to use, because for example the collapse of where
where  is inaccessible, is the proof-theoretic ordinal of Kripke-Platek + “the class of ordinals is recursively inaccessible”, so the system Kripke-Platek + “there exists a recursively inaccessible ordinal” has precisely the strength to prove that the ordinal notation system makes sense.
is inaccessible, is the proof-theoretic ordinal of Kripke-Platek + “the class of ordinals is recursively inaccessible”, so the system Kripke-Platek + “there exists a recursively inaccessible ordinal” has precisely the strength to prove that the ordinal notation system makes sense.
The need for large cardinals/large recursive ordinals is causing problems for me in trying to create my own extensions of the -reflecting ordinal notation. Since that notation has one thinning operation, the natural extension would be to have many; for that, I imagine we could have a thinning operation of
-reflecting ordinal notation. Since that notation has one thinning operation, the natural extension would be to have many; for that, I imagine we could have a thinning operation of  -indescribability for each
-indescribability for each  , rather than just stationarity. But then, I want to extend to many variables, so I want some notion of
, rather than just stationarity. But then, I want to extend to many variables, so I want some notion of  -indescribability, and then perhaps
-indescribability, and then perhaps 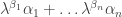 -indescribability for some dominating ordinal
-indescribability for some dominating ordinal  , mirroring the notation for the Bachmann-Howard ordinal. But I don’t know any large cardinal hierarchy that suffices. So I’m at the mercy of what large cardinal notions are available, which is frustrating since all I really care about is the relative size of these large ordinals, and not their large cardinal properties.
, mirroring the notation for the Bachmann-Howard ordinal. But I don’t know any large cardinal hierarchy that suffices. So I’m at the mercy of what large cardinal notions are available, which is frustrating since all I really care about is the relative size of these large ordinals, and not their large cardinal properties.
Gro-Tsen, your article on ordinal collapsing functions was key for my current curiosity. Splendid work!
John asked about ordinal collapsing functions:
I had the same question nagging me, and begun to call it a working hypothesis instead. I’m still trying to wrap my head around the cool discussion following your head-on question. You people are too generous!
Those are really cool links, Royce Peng! I’ll need some time for those. Soon. And to spend some more on googlogy. And to write a post on oodle theory…
Thanks! Oodle theory was actually created by a friend of mine. I’d be genuinely interested in what logicians would think about oodle theory philosophically. It was created for the purpose of the “Name the largest number” game, but it is potentially more significant than that, since it concerns truth and expressivity of set theory.
The multi-variable Veblen hierarchy really reminds me of Jonathan Bowers’ notation for large numbers, which eventually starts using multidimensional arrays.
After all, does the sequence of indices have to be simply infinite? It could have a structure of a general ordinal itself, where ordinals beyond can be expressed on two lines, ordinals below
can be expressed on two lines, ordinals below 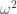 as a 2-dimensional matrix of indices, orginals below
as a 2-dimensional matrix of indices, orginals below  as a 3-dimensional matrix…
as a 3-dimensional matrix…
Yes, you could certainly write ordinals that way! But there is a better notation for transfinite indices, which I imagine John will describe in his next article.
Royce: this next article may take years to appear, so let me ask: what exactly are you talking about?
I was thinking about Schutte’s notation (which is referred to as Klammersymbole) that looks like:
where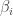 refers to the index of the variable
refers to the index of the variable 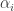 . Or we could use Veblen’s notation of
. Or we could use Veblen’s notation of  , but it’s pretty similar. (Veblen’s notation has some peculiarities that I’d rather avoid, but we could use the same format.)
, but it’s pretty similar. (Veblen’s notation has some peculiarities that I’d rather avoid, but we could use the same format.)
From your previous articles it looked like you were going to go up to the Large Veblen ordinal, but perhaps I was being presumptuous.
Well, if it will take several years, it should be calle “Large Countable Ordinals, Part “.
“.
Hello, I have a question on fixed points for the multivariate Veblen functions.
Is it true that all of the following are equal to ?
?
a) ?
? ?
? ?
?
b)
c)
I think the answer is yes – to get different numbers you would have to add a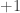 in analogy with
in analogy with 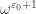 , so
, so 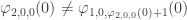 , for example.
, for example.
Thank you!
Rob
Yes, all true.
Thank you Royce!
One follow up if you don’t mind.
Does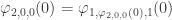 ?
?
No; if , then by definition
, then by definition
Over on G+, Pol Nasam asked some interesting questions:
An ordinal is computable or if we can find a 1-1 correspondence between ordinals less than
is computable or if we can find a 1-1 correspondence between ordinals less than  and natural numbers and write a computer program that decides whether the
and natural numbers and write a computer program that decides whether the  th of these ordinals is less than the
th of these ordinals is less than the  th one.
th one.
When is
is  this is trivial, because we can say the
this is trivial, because we can say the  th ordinal less than
th ordinal less than  is just
is just 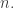
The fun starts with larger countable ordinals where we need more cleverness to find a 1-1 correspondence between ordinals less than
where we need more cleverness to find a 1-1 correspondence between ordinals less than  and natural numbers.
and natural numbers.
In these more interesting cases, the 1-1 correspondence cannot be order-preserving.
There is a countable ordinal called the Church–Kleene ordinal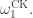 Every ordinal less than the Church–Kleene ordinal is computable. But Church–Kleene ordinal itself is not computable, and neither is any larger ordinal.
Every ordinal less than the Church–Kleene ordinal is computable. But Church–Kleene ordinal itself is not computable, and neither is any larger ordinal.
Yes, this is exactly what the continuum hypothesis says.
I know what you mean by saying that the game becomes boring, but I think that’s wrong. It’s not boring, it’s fascinating!
It’s fascinating because even though the structure of computable ordinals seems boringly repetitive, it’s impossible to get a complete precise grasp on “the large-scale structure of all of them”.
Of course there’s a lot we can say about them. Every ordinal is either zero, a successor ordinal, or a limit ordinal. Cantor normal form helps us understand the ordinals in a more detailed way, and Veblen normal form helps us even more. But none of these ideas give a complete picture of the computable ordinals!
One keeps thinking… for a while, anyway… that one should be able to develop a complete picture of all the computable ordinals. But what’s a ‘complete picture’? It might mean a notation that allows you to name all such ordinals and decide which one is bigger than which. You might also want to know how to do arithmetic with all these ordinals.
That would be nice. But unfortunately while this is possible for all ordinals less than any particular computable ordinal, it’s not possible for all computable ordinals! The reason is that the Church–Kleene ordinal is not itself computable.
What does this mean, actually? It means that as we go to larger and larger computable ordinals, we need to keep developing more and more clever notations. There cannot be any completely systematic way to proceed all the way up to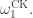 New ingenuity keeps being required!
New ingenuity keeps being required!
Indeed it seems that right now, the only important application of large computable ordinals is to measure the strength of formal systems. But I bet there are other applications that have not yet been discovered.
If you play the game and find yourself repeating the same procedure over and over again, then you’re doing it wrong – or at least, you could be doing it better, since you could just describe the procedure and take the infinite limit.
Of course, you might then start describing a procedure, taking the limit, describing a procedure, taking the limit… and this might actually be the start of a larger procedure that you could take the limit of! So, the game is very much trying to think “outside of the box” that your procedures are currently stuck in – but the first step is to recognize the box that you’re in.
I think if I were to play this game with no knowledge about large ordinal notations, I would probably do better than the average joe, but I doubt I would get as far as the Bachmann-Howard ordinal – maybe not even the Small Veblen ordinal. But once you see the construction, it is quite simple. So this really is a game of having good ideas, not just repeating the same thing over and over.
All of that goes for the “name the largest natural number you can” game as well. But people think that that game is stupid, because “You can always just add one.”
Here are some applications of / problems involving large countable ordinals.
John has already mentioned their use in ordinal analyses of various theories. It should be pointed out that the purpose of an ordinal analysis is more than just finding the proof theoretic ordinal of the theory, according to the people who do them – but I’m not really equipped to expound further on this.
You also seem some large countable ordinals in papers about term rewriting systems. Lepper has written a nice survey dissertation on the subject. Large countable ordinals appear both in the order types of these systems, and in their depth and size complexity. Apparently the order types of totally terminating rewrite systems are upper bounded by the Small Veblen ordinal, and their depth complexity is upper bounded by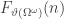 . According to Andreas Weiermann’s paper on the Hydra battle, any natural pointwise termination ordering for the Hydra battle rewrite system must have order type equal to the Bachmann–Howard ordinal. So some large countable ordinals do appear in this subject.
. According to Andreas Weiermann’s paper on the Hydra battle, any natural pointwise termination ordering for the Hydra battle rewrite system must have order type equal to the Bachmann–Howard ordinal. So some large countable ordinals do appear in this subject.
The partition calculus is basically Ramsey theory for infinite ordinals and cardinals, so countable ordinals are found here as well. Andres Caicedo has a nice post about them; here is a paper he has written on the subject.
John has mentioned the exponential polynomials of Skolem in the comments of another article in this series, and I have mentioned fusible numbers; both structures are conjectured to have order type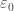 , but both are open problems.
, but both are open problems.
The ordinals can be given the operations of nimber addition and nimber multiplication, and this turns the ordinals into a proper class field. A natural question to ask is which ordinals form algebraically closed fields. Conway proved that the algebraic closure of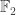 is
is 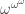 , so that is the smallest one; Hendrik Lenstra talks about it in Nimber Multiplication, and conjectures that the next algebraically closed ordinal is the Small Veblen ordinal. (he gives an unusual notation for it in the paper.)
, so that is the smallest one; Hendrik Lenstra talks about it in Nimber Multiplication, and conjectures that the next algebraically closed ordinal is the Small Veblen ordinal. (he gives an unusual notation for it in the paper.)
If we let LO be the class of countable linear orders, and we order LO by embeddability, then Fraisse’s conjecture states that LO is a well-quasi-order under this ordering. This conjecture was proven by Richard Laver (in fact, he proved that LO was a BQO). In this paper by Marcone and Montalban, they define the Hausdorff rank of a linear order, which will be some ordinal, and define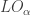 to be the set of countable linear orders with Hausdorff rank less than
to be the set of countable linear orders with Hausdorff rank less than  . They also define the length of a WQO to be the supremum of the order types of all linear extensions of the WQO. The question they then ask is, “What is the length of
. They also define the length of a WQO to be the supremum of the order types of all linear extensions of the WQO. The question they then ask is, “What is the length of 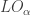 for various ordinals
for various ordinals  ?” They show that
?” They show that  has length
has length  , interestingly enough, which they use to show that Fraisse’s conjecture restricted to linear orders of finite Hausdorff rank is provable in
, interestingly enough, which they use to show that Fraisse’s conjecture restricted to linear orders of finite Hausdorff rank is provable in  “
“ is well-ordered”. But the lengths of other
is well-ordered”. But the lengths of other 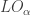 is an open problem as far as I know.
is an open problem as far as I know.
If I think of other examples, I’ll let you guys know.
By the time your post reached me (my blog, and my email) the non-working links were actually missing. So I can’t fix them without some help.
For example:
If you post the URLs for those missing links, I’ll stick them in your original comment, and delete our little discussion here, and everything will seem perfect to people who read this conversation in the 25th century: they’ll never know we weren’t perfect!
I cannot wrap my head around the fact that the ordinals of this series are countable and yet “Peano arithmetic is powerful enough to work with ordinals up to but not including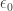 ”..
”..
Maybe it’s because you haven’t internalized the ideas surrounding Gödel’s incompleteness theorem, which says there are lots of questions about arithmetic that aren’t decidable in Peano arithmetic.
In fact, there are lot of ‘obviously true’ statemements about arithmetic that are not provable in Peano arithmetic! The most famous example is the fact that every Goodstein sequence is eventually zero—or in other words, you can always win the game Hercules and the Hydra (click on the link to actually play the game). This is a fairly down-to-earth fact about arithmetic that is easy to understand, easy to prove using induction up to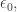 but not provable in Peano arithmetic.
but not provable in Peano arithmetic.
Why can’t we formalize induction up to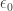 in Peano arithmetic? It’s because Gentzen proved the consistency of Peano arithmetic using induction up to
in Peano arithmetic? It’s because Gentzen proved the consistency of Peano arithmetic using induction up to  If Peano arithmetic could handle induction up to
If Peano arithmetic could handle induction up to 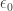 it could prove itself consistent. By Gödel’s second incompleteness theorem this would imply Peano arithmetic is inconsistent!
it could prove itself consistent. By Gödel’s second incompleteness theorem this would imply Peano arithmetic is inconsistent!
Even crazier, any recursively enumerable and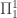 -sound theory cannot handle recursive ordinals past a certain point, i.e. it cannot prove large recursive ordinals are indeed well-ordered. So, if ZFC+I0 is
-sound theory cannot handle recursive ordinals past a certain point, i.e. it cannot prove large recursive ordinals are indeed well-ordered. So, if ZFC+I0 is 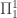 -sound, it cannot prove sufficiently large recursive ordinals are well-ordered!
-sound, it cannot prove sufficiently large recursive ordinals are well-ordered!
Cool! Take one of those recursive ordinals. Could we argue that there are recursively enumerable extensions of ZFC+I0 that can prove that ordinal is well-ordered? Could we argue that one of these must be an extension of the form ZFC+X where X is a large cardinal axiom even strong than I0?
My ‘reasoning’, if you want to dignify it by that name, is very sketchy here—especially in the second step, which relies on the hope that large cardinal axioms are all we ever need to prove that larger and larger recursive ordinals are well-ordered. And I’m leaving out the stuff about -soundness, mainly because I’m not smart enough to see its role. Feel free to stick it in if it helps!
-soundness, mainly because I’m not smart enough to see its role. Feel free to stick it in if it helps!
I’m mainly just wondering if the ‘inexhaustibility’ of large recursive ordinals can be fed back somehow to get a corresponding ‘inexhaustibility’ of large cardinal axioms.
Certainly there are recursively enumerable extensions of ZFC+I0 that prove an ordinal is well-ordered, because we could brutishly add the axiom “
is well-ordered, because we could brutishly add the axiom “ is well-ordered”! But, whether this can be done with large cardinal axioms only is a very interesting question. A major problem is that the term “large cardinal axiom” is not really a formally defined term. I’m sure there have been attempts to rigorously define the notion of LCA, for example I believe Woodin has attempted a definition; but I don’t know how successful any such attempts are considered to be. I imagine Andres would know more about this, if he reads this post. Also, there might be more information if we replace “prove all recursive ordinals are well-ordered” with “prove all arithmetic sentences” or “prove all sentences in (class F)”.
is well-ordered”! But, whether this can be done with large cardinal axioms only is a very interesting question. A major problem is that the term “large cardinal axiom” is not really a formally defined term. I’m sure there have been attempts to rigorously define the notion of LCA, for example I believe Woodin has attempted a definition; but I don’t know how successful any such attempts are considered to be. I imagine Andres would know more about this, if he reads this post. Also, there might be more information if we replace “prove all recursive ordinals are well-ordered” with “prove all arithmetic sentences” or “prove all sentences in (class F)”.
A possibly interesting wrinkle: In ZFC, we know that the large cardinal axioms have an upper bound of since this has been proven to be inconsistent. But that axiom has not been proven to be inconsistent in ZF, so
since this has been proven to be inconsistent. But that axiom has not been proven to be inconsistent in ZF, so  could well be consistent, and even
could well be consistent, and even 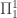 -sound, so it would have a recursive proof-theoretic ordinal; so the march toward the Church-Kleene ordinal continues onward in ZF, whereas that march in ZFC has already finished down below! I guess that’s not paradoxical, but it’s certainly an interesting twist.
-sound, so it would have a recursive proof-theoretic ordinal; so the march toward the Church-Kleene ordinal continues onward in ZF, whereas that march in ZFC has already finished down below! I guess that’s not paradoxical, but it’s certainly an interesting twist.
Concerning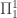 -soundness: In Rathjen’s “The Realm of Ordinal Analysis” (see https://www1.maths.leeds.ac.uk/~rathjen/realm.pdf), he proves (Theorem 2.21) that
-soundness: In Rathjen’s “The Realm of Ordinal Analysis” (see https://www1.maths.leeds.ac.uk/~rathjen/realm.pdf), he proves (Theorem 2.21) that
i) If a theory T is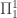 -sound, its proof theoretic ordinal is less than the Church-Kleene ordinal
-sound, its proof theoretic ordinal is less than the Church-Kleene ordinal
ii) If a theory T contains and its proof theoretic ordinal is less than the Church-Kleene ordinal, then T is
and its proof theoretic ordinal is less than the Church-Kleene ordinal, then T is 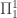 -sound.
-sound.
But part ii) means that, if we have a theory T that is at least as strong as , then all we have to do is add some
, then all we have to do is add some 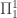 axiom that is false for the natural numbers; this makes T
axiom that is false for the natural numbers; this makes T 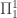 -unsound, so by part ii) its proof theoretic ordinal must be the Church-Kleene ordinal! For example,
-unsound, so by part ii) its proof theoretic ordinal must be the Church-Kleene ordinal! For example, 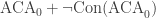 will work just fine.
will work just fine.
Derivative? You say it’s popular? Who {cursing removed} came up with the idea of calling f’ ‘derivative’? It’s where I see your later remark hit a nail straight:
(Did I see you use that exact wording before?)
However, in this case I really like the irony the word brings into this particular discourse. It’s also a nice surreal defense against part-time disbelievers.
Noooo!
Haha, good one! I find it quite remarkable how neat and orderly things get with a sufficiently powerful notation, considering the complications without.
Oh cool, there’s even a lookout section where these get mentioned. And proof theory! I’m enthused!
While we’re at it, thanks for digging up the more recognizable name for what has been haunting me earlier. And especially for the nice listings. And puzzles!
for what has been haunting me earlier. And especially for the nice listings. And puzzles!
Refurio wrote:
Yes, I’ve written about this material before in various places (“week236” of This Week’s Finds, and my bigness series on G+), so here I’m just trying to organize that material, explain it better, and go a wee bit further. I’m reusing all the jokes that seemed funny the first time I made them. As my father-in-law used to say, “a good joke, like wine, improves with age”. But mainly for the person telling it.
I think a jusification for the word ‘derivative’ might be the following: that you are deriving f’ from f, and, besides, f’ tells you informatoin about the speed of f, as you get to know its fixed points!
David Madore (aka Gro-Tsen) sent me a very interesting email, which he’s given me permission to quote here:
Very nice! I would very much like to see this countable ordinal roadmap, is there any way to post or upload it?
I hadn’t known that computation models that compute over transfinite times had been described prior to Hamkins and Lewis’s Infinite Time Turing Machines. Gro-Tsen, do you know where the supremum of the writable ordinals, eventually writable ordinals, and accidentally writable ordinals fall in the zoo of large countable ordinals?
Concerning the “normal variant” of ordinal collapsing function, it does seem to be the preferred variant nowadays. Note that, while the collapsing function is no longer continuous or monotonic, it does become one-to-one, which is nice. Also, I like the fact that for instance is the fixed point free version of the
is the fixed point free version of the  function up to
function up to 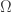 , whereas the old variant gets stuck at
, whereas the old variant gets stuck at  . So I think I prefer the normal variant, although I guess it’s a matter of taste.
. So I think I prefer the normal variant, although I guess it’s a matter of taste.
I just posted a link to the roadmap in a nearby comment.
Concerning the transfinite computability (α-recursion) studied in the golden age of higher computability theory, nobody seems to have explicitly formulated it in terms of transfinite “machines” at the time, but the translation is extremely obvious, especially when looking at the formulation in the last chapter of Hinman’s book (which, incidentally, is available here): see this MathOverflow question where I make it a little bit more explicit (I really don’t think I invented anything there: this way of viewing computable functions as programs seemed completely natural to me when I read the book and I can’t imagine that it wasn’t in Hinman’s mind). It’s a bit like reading Hofstadter’s BlooP and FlooP programming languages from a description of primitive recursive and general recursive functions.
Anyway, I’m not saying that Infinite Time Turing Machines and similar concepts are “nothing new under the sun”, but I’m still perplexed by the lack of reference or connection to the “golden age” literature. Koepke has a few papers which refer to Sacks’ book (Higher Recursion Theory, 1990, I guess that’s very late golden age…), but nobody seems to have drawn a precise comparison with the distinctly operational definitions given in Hinman’s book or Simpson’s “short course”. (Subjectively, I much prefer to think of transfinite computation as a programming language which can perform transfinite loops and handle transfinite variables, à la BlooP/FlooP, than insist on copying the Turing machine paradigm.) The best I could find are the two surveys by Dag Normann (“Higher generalizations of the Turing Model”) and P.D. Welch (“Transfinite machine models”) in the Turing’s Legacy volume (Downey ed., Cambridge LNL 42, 2014), but even then, the first is mostly about what I called the “golden age” above and the second is mostly about “modern” transfinite computation models, and they draw little connections between the two, beyond citing each other’s paper…
Royce wrote:
Since Gro-Tsen has a lot of material on his blog, but hasn’t publicized this, I will wait to see what he says. I’d be happy to put it on my website, but since it seems to be a document subject to revision, it probably makes more sense for him to put it someplace where he can revise it ad libitum.
Here is a permanent link and here is a Git repo for the source in case someone wants to send me patches or pull requests.
Thanks for doing that! I have some comments to make on that email of yours I posted, but today I want to finish a paper on topological crystals, which I’m writing with Greg Egan.
Gro-Tsen wrote:
To me this is one of the most tantalizing aspects of the whole subject. We seem to have ‘worlds within worlds’, with phenomena in the larger worlds being reflected in the smaller ones.
Here’s my best attempt at an explanation. All we really deal with in mathematics are finite strings of symbols, which in most cases are fairly short. We cleverly use them to talk about much larger objects… so perhaps it’s not so surprising that when we try to name the largest objects we can, whether finite, countable or uncountable, we tend to reuse the same tricks.
However, I wish we had a clearer theory of what’s going on here. A philosophical explanation of it is not as satisfying as a bunch of theorems!
On the topic of those four levels (quickly growing sequences of large integers, computable ordinals, large countable ordinals, cardinals) and correspondances between them, I’d like to link to the blog entry of David Madore where he writes about that topic, because it’s not easy to find from here:
• David Madore, Qui peut dire le nombre le plus grand?
I was tinkering with computer programs for ordinal notations in the late 60’s. I don’t think I have any of the code any more. I do remember that it was written in Lisp. The first notation was the usual omega-polynomials, and I implemented comparison, addition, multiplication and exponentiation. Later I invented notation based on the Veblen hierarchy. Veblen based his hierarchy on omega-powers to invent new ordinals at the lowest steps of his hierarchy,, but I noticed it could even be done with just successor. But I never graced this stuff with any running code. I found some notebooks about this stuff while cleaning house preparatory to moving, but I never put any of it in machine-readable form. What kept happening when I tried writing it up was that I kept finding new generalizations so I could make it more general, and I ended up choking on mental generalisation recursion. Of course, that is what ordinals are about.
I also recently wrote a computer program that writes a long piece of text (in nanowrimo it would count as a novel because it is 50000 words, but I won’t grace it with such a title) in which I have John Baez counting ordinals far past the heat-death of the universe. It’s a large pdf, and I’m looking for an appropriate place to post it. If I make it available on my home server, I fear that a flood of requests would take the server down — it’s 265194 bytes and I have only a home DSL line connecting me with the world. The .tex output is bigger — 642522 bytes) The code that generates it is quite reasonably sized. See it at https://github.com/hendrikboom3/Text-generation
I don’t think you need to fear a “flood of requests” for a novel about me counting ordinals far past the heat death of the universe, and 265 kilobytes isn’t huge by today’s standards. But if you want, you can email it to me and I can put it on my website.
Very neat. I didn’t know the fixed point theorem is due to Veblen.
I came across the following document
Click to access ordtrees.pdf
which is a really interesting document that maps tree diagrams to ordinals up through the Small Veblen Ordinal.
I would love to be able to take any random tree and understand which ordinal it represents, and to take any ordinal and know how to draw its tree…but am I right in thinking this is not very straightforward? I can notice some patterns, but I don’t think there are simple rules…unless someone else can see something I am not?
Thanks a lot!
Rob
I can give an approximate answer.
Let be the ordinal corresponding to the tree with n children corresponding to the ordinals
be the ordinal corresponding to the tree with n children corresponding to the ordinals 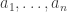 . So for example if we take the tree with 3 children, each of which has 3 leaf children, it’s corresponding ordinal will be
. So for example if we take the tree with 3 children, each of which has 3 leaf children, it’s corresponding ordinal will be 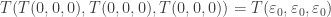 . Then we cannot give simple expressions for T involving the n-ary Veblen function, because Jervell’s ordering implies that
. Then we cannot give simple expressions for T involving the n-ary Veblen function, because Jervell’s ordering implies that  will be larger than any of the
will be larger than any of the 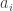 , whereas the n-ary Veblen function will have fixed points. Still, we can have approximate expressions for T, which will be accurate except near fixed points of the expressions.
, whereas the n-ary Veblen function will have fixed points. Still, we can have approximate expressions for T, which will be accurate except near fixed points of the expressions.
We have:
For ,
,  except near fixed points.
except near fixed points.
For ,
,  except near fixed points.
except near fixed points.
Note that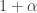 is
is  when
when  is finite, and
is finite, and  when
when  is infinite.
is infinite.
Perhaps Gro-Tsen can describe exactly how to handle the “bump near fixed points”.
Thank you very much Royce! This is really helpful.
I am hoping you could help me work through what seems to be a simple example, but I can’t get my head around it at the moment. The tree for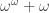 — I can’t work out which values of
— I can’t work out which values of  and
and 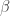 would make it look the way it is in the example. I think it’s maybe because I am not super-fluent in ordinal arithmetic.
would make it look the way it is in the example. I think it’s maybe because I am not super-fluent in ordinal arithmetic.
Gro-Tsen, I didn’t realise you were the author of this paper! Any more detail you have about how you generated so many of these examples, and any refinement to the above rules, especially around fixed points, would be very helpful.
Thank you both,
Rob
I should say that on the above, the closest I got was so the left branch of the first bifurcation (the bottom one) is as it is, but then I would expect
so the left branch of the first bifurcation (the bottom one) is as it is, but then I would expect  for the right branch, so that you get
for the right branch, so that you get  , but this would imply that the right branch has an extra segment below the
, but this would imply that the right branch has an extra segment below the  , to represent the
, to represent the 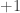 in the
in the 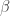 , but it doesn’t…it just seems to be
, but it doesn’t…it just seems to be  .
.
Hope that is clear – it’s hard to describe the tree in text format!
This is a case of the fixed point problem; for A = (0,(1,0)) (Here a natural number n means a path of length n, so (1,0) is a tree where the root has two children, and the left child has a child.) the formula gives , which it can’t be since
, which it can’t be since  and
and  .
.
A general rule is that if A = (X,Y), B is formed by repeatedly taking B -> (B) or B -> (Z,B) with Z < X (so the right child of any node in B will be less than X), and C is formed by attaching A to the rightmost leaf of B, then T(C) = T(A) + T(B). So in the example of A = (1,0), B = (0,0), we get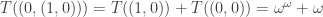 . Also, B can be replaced by anything generated by B -> (B) and B -> (0,B), so for example we could take B = (0, (((0, ((0,((0)))))))) and C = B = (0, (((0, ((0,(((1,0)))))))))we would still get T(C) = T(A) + T(B).
. Also, B can be replaced by anything generated by B -> (B) and B -> (0,B), so for example we could take B = (0, (((0, ((0,((0)))))))) and C = B = (0, (((0, ((0,(((1,0)))))))))we would still get T(C) = T(A) + T(B).
I’m afraid I’ve forgotten all about this particular representation of ordinals, so I can’t really help you (in fact, I’d be a little amazed if it turned out there were no mistakes in this huge list which I generated by hand). The answer is probably in Andreas Weiermann’s 1993 paper “An Order-Theoretic Characterization of the Schütte-Veblen Hierarchy” or his joint paper with Rathjen in the same year, “Proof-Theoretic investigations on Kruskal’s theorem”, but I admit I don’t really remember what this is all about.
There are also some questions which I think are very connected when you try to define ordinal notations (up to the small or large Veblen ordinals) using Veblen functions of several variables. Schütte’s 1954 paper, “Kennzeichnung von Ordnungszahlen durch rekursiv erklärte Funktionen” (in German, obviously) does a very nice job of explaining how you can have several variants of his Klammersymbol (parenthesis-symbol) which differ essentially in the way they handle fixed points—and how to convert from one to another.
Thank you Royce and Gro-Tsen – all very helpful! I found some additional very detailed explanation of this particular ordering (focusing on ordinals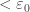 , but hopefully extrapolatable to ordinals up to the small Veblen ordinal) in case anyone is interested. It covers ordinal trees that contain fixed points and then goes on to explain the fixed-point free ordering and rules in a lot of detail, pages 41-50. The author is Alfred Bratterud.
, but hopefully extrapolatable to ordinals up to the small Veblen ordinal) in case anyone is interested. It covers ordinal trees that contain fixed points and then goes on to explain the fixed-point free ordering and rules in a lot of detail, pages 41-50. The author is Alfred Bratterud.
https://www.duo.uio.no/handle/10852/8742
I really appreciate that you have taken the time to answer my questions — and thank you John for a fantastic series of posts!
Dear John Baez,
I have corresponded with you a few years ago and had a satisfactory reply (see page 24 of Brain 1). I think you are a very versatile mathematician and in my old age (90) I am still doing a lot. You can find a little more about my work from the internet. I was a student of Einar Hille at Yale.
The main reason for my writing you is that I think I have been an early developers of a theory of the brain that involves to a limited degree the use of quaternions and octonions by the neurons of the brain. It is not so much the algebra but the interpretation of how we come about to behave in a noncommutative and non associative ways. My two papers on the brain have been recently published in Neural Networks. I think it is best to show you some works and acknowledgements I have received, so if you find it sufficiently interesting, you can advise me if possible what you think is best to work on next in this subject and where I can turn to get some useful help. I believe that the interest in physics with dimensions arises from the workings of our neurons and not simply an act of imagination. I apologize deeply for bothering you with your so many interests.
With kind regards,
Tom Saaty
This thread on large ordinals is not the best place to talk about neural networks. If you email me your papers I’ll be glad to look at them.
I’ve wondered for a while if ordinal numbers are equivalent to the “extra” numbers you get in nonstandard models of arithmetic. If I remember right from GEB these nonstandard models include numbers that encode proofs of Gödelian statements that assert their own unprovability, and the only way contradiction is avoided is if these numbers thwart inductive arguments by being too large to count to.
After reading your recent posts my guess is that these are not ordinal numbers, and if they exist in your model they’re included in the set omega = {0,1,2,…}
The “extra” natural numbers in nonstandard models of arithmetic can’t be ordinals, in the following sense: in a model of arithmetic every number except zero is a successor, but is not a successor.
is not a successor.
That makes sense, thanks!
Actually I should expand on my comment a bit, to make it clearer.
In a model of arithmetic every number except zero is a successor, so every nonstandard natural number gives an infinite descending sequence
gives an infinite descending sequence
(If this sequence reached zero after finitely many steps, would be standard.) But as explained earlier on this blog, there are no infinite strictly decreasing sequences of ordinals.
would be standard.) But as explained earlier on this blog, there are no infinite strictly decreasing sequences of ordinals.
Note that we study models of arithmetic within set theory, where we have a way to say what the ‘standard’ natural numbers are. This allows us to say things like “if the sequence reached zero after finitely many steps” and have it mean something: it means after a standard number of steps.
Right. More precisely, we have a limited ability to work with ordinals within Peano arithmetic. We cannot do much with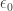 or larger ordinals in this theory, because
or larger ordinals in this theory, because 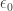 is the proof-theoretic ordinal of Peano arithmetic. But we can work with any smaller ordinal
is the proof-theoretic ordinal of Peano arithmetic. But we can work with any smaller ordinal  by putting its members in one-to-one correspondence with natural numbers and defining a new
by putting its members in one-to-one correspondence with natural numbers and defining a new 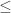 relation on the natural numbers to describe the ordering of
relation on the natural numbers to describe the ordering of 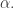 (For
(For 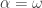 , which is the case you’re mainly talking about, we can use the identity map as our one-to-one correspondence and the ‘new
, which is the case you’re mainly talking about, we can use the identity map as our one-to-one correspondence and the ‘new  relation’ is the ordinary
relation’ is the ordinary  relation. But let’s be more general.)
relation. But let’s be more general.)
If we now take a nonstandard model of Peano arithmetic, everything we can do with the ordinal has a nonstandard interpretation. It will have more members, just as you say. These will be nonstandard natural numbers, reinterpreted as members of
has a nonstandard interpretation. It will have more members, just as you say. These will be nonstandard natural numbers, reinterpreted as members of 
I loved John Baez’s three-part system on large countable ordinals (1, 2, 3) but something nagged at me. It felt like a description of an algorithm in prose, and I feel like I don’t really understand an algorithm until I’ve implemented it. But what does it mean to implement an ordinal?
I found a couple of answers to that online. One is the definition of a recursive ordinal, and the other is Kleene’s O. However both seemed pretty unsatisfactory to me; I wanted something that could naturally express operations like addition/multiplication/exponentiation, as well as expressing finite ordinals.
Your exposition is interesting, direct, and illustrative of expansion of comprehension, and via deductive inference.
Ah, but what if the empty set (as ordinal zero) is the smallest set and ordinal that can be defined without self-reference.
Also, what if it can’t?
Some don’t necessarily have well-foundedness (restriction of comprehension) as axiomatized. Then “sets” as they are (as defined by their members and membership) are “purely logical” to fulfill sets that are, and sets that aren’t.
You might notice identity of f(x) = x is “continuous”, but the countable ordinals don’t have a fixed point (or rather, it would be a countable ordinal).
You might also be interested in Scott’s box and circle notation(s), then for notions of collapse as via model collapse or Skolem/Levy. This has collapse implementing the same notion as a “point at infinity” (or fixed point), and box and circle for variously the monotone and uniform.
As you can see, the mathematically infinite lends itself to many and varied extensions (and for each extension, collapse), where then the point is to figure out what to make of the infinite both in terms of the unbounded and large, or, effectively infinite, or, the non-finite and truly infinite, for applications. As some will have a mathematical theory of physics, the “truly infinite” as mathematical is relevant to the applied.
Here all of the trans-finite and large cardinals has all its application collapsed to a countable infinite fixed point, at infinity, or “\infty”. A usual goal is the understanding of the variously physical or mathematical significance of “infinity” in the equations (or increases without bound of relations), and the replacement of that value (or process) with an approximant (usually as of the first few terms of an equivalent series expansion). The requirement for application of infinity is how all the terms drop out as they algebraically reach identity, equality, or tautology, not just the leading terms as provide very accurate estimations of results of combined measurements.
Thank you for letting me post to your blog and I hope your readership finds its validity and of what use it is.
On Google+, Cody Roux wrote a very interesting comment about ordinal analysis and the TCLA list of open problems:
Maybe the following is of some interest. Problem 26 has been solved using certain collapsing techniques for Gödel’s T in the formulation with combinators. The problem of Barendregt concerns the extension to T with respect to lambda terms. What is available is here is a method mapping sequences of rewritten terms to ordinals such that longer and longer sequences get smaller and smaller ordinals. Still missing is the natural assignment of ordinals to terms.
Getting back to the Paris-Harrington theorem: the original proof used non-standard models of PA. (Kanamori and McAloon soon simplified it; the treatment in the recent book by Katz and Reimann is particularly easy to follow.) That’s the one I want to look at here.
But since you had such fun with ordinals here (and here and here), I better add that Ketonen and Solovay later gave a proof based on the ε0 stuff and the hierarchy of fast-growing functions. (The variation due to Loebl and Nešetřil is nice and short.) We should talk about this sometime! I wish I understood all the connections better. (Stillwell’s Roads to Infinity offers a nice entry point, though he does like to gloss over details.)
So, I’m not sure to what extent this is a thing. John Baez mentions in this blog post that common large countable ordinals beyond the large Veblen ordinal can also “be defined as fixed points”. He doesn’t expand on that but I take it that means fixed points of a further Veblen-like / klammersymbol-like construction.
But, I haven’t been able to find any good account of this. Is this a known/standard thing? I want to know just how far the Veblen construction can be pushed — like, beyond the large Veblen ordinal, is there an “ultimate Veblen ordinal” somewhere; and might it be equal to an already-named / well-known one, such as Bachmann-Howard? (I suppose a negative answer here would be if arbitrarily large computable ordinals could be obtained this way, making the “ultimate Veblen ordinal” just .)
.)
Now I can certainly think of ways of continuing beyond the large Veblen ordinal myself… but I don’t really want to reinvent the wheel here when I expect others have likely already done it better. So, is there a good account of this somewhere?
[…] I would appreciate feedback on the following attempt to write large countable ordinals (& the functions that generate them) in Conway notation (my primary source of information in creating these constructions was Large Countable Ordinals): […]