Last time I took you on a road trip to infinity. We zipped past a bunch of countable ordinals
and stopped for gas at the first one after all these. It’s called Heuristically, you can imagine it like this:
More rigorously, it’s the smallest ordinal obeying the equation
Beyond εo
But I’m sure you have a question. What comes after ?
Well, duh! It’s
Then comes
and then eventually we get to
and then
and after a long time
and then eventually
and then eventually….
Oh, I see! You wanted to know the first really interesting ordinal after
Well, this is a matter of taste, but you might be interested in This is the first ordinal after
that satisfies this equation:
How do we actually reach this ordinal? Well, just as was the limit of this sequence:
is the limit of this:
You may wonder what I mean by the ‘limit’ of an increasing sequence of ordinals. I just mean the smallest ordinal greater than or equal to every ordinal in that sequence. Such a thing is guaranteed to exist, since if we treat ordinals as well-ordered sets, we can just take the union of all the sets in that sequence.
Here’s a picture of taken from David Madore’s interactive webpage:
In what sense is the first "really interesting" ordinal after
?
For one thing, it’s first that can’t be built out of and
using finitely many additions, multiplications and exponentiations. In other words, if we use Cantor normal form to describe ordinals (as explained last time), and allow expressions involving
as well as
and
we get a notation for all ordinals up to
What’s the next really interesting ordinal after ? As you might expect, it’s called
This is the next solution of
and it’s defined to be the limit of this sequence:
Maybe now you get the pattern. In general, is the
th solution of
We can define this, if we’re smart, for any ordinal
So, we can keep driving on through fields of ever larger ordinals:
and eventually
which is the first ordinal bigger than
Let’s stop and take a look!
Nice! Okay, back in the car…
and then
and then
As you can see, this gets boring after a while: it’s suspiciously similar to the beginning of our trip through the ordinals. The same ordinals are now showing up as subscripts in this epsilon notation. But we’re moving much faster now, since I’m skipping over much bigger gaps, not bothering to mention all sorts of ordinals like
Anyway… while we’re zipping along, I might as well finish telling you the story I started last time. My friend David Sternlieb and I were driving across South Dakota on Route 80. We kept seeing signs for the South Dakota Tractor Museum. When we finally got there, we were driving pretty darn fast, out of boredom—about 85 miles an hour. And guess what happened then!
Oh — wait a minute—this one is sort of interesting:
Then come some more like that:
until we reach this:
and then
As we keep speeding up, we see:
So, anyway: by the time we got that tractor museum, we were driving really fast. And, all we saw as we whizzed by was a bunch of rusty tractors out in a field! It was over in a split second! It was a real anticlimax — just like this anecdote, in fact.
But that’s just the way it is when you’re driving through these ordinals! Every ordinal, no matter how large, looks pretty pathetic and small compared to the ones ahead — so you keep speeding up, looking for something ‘really new and different’. But when you find one, it turns out to be part of a larger pattern, and soon that gets boring too.
For example, when we reach the limit of this sequence:
our notation fizzles out again, since this is the first solution of
We could make up a new name for this ordinal, like I don’t think this name is very common, though I’ve seen it. We could call it the Tractor Museum of Countable Ordinals.
Now we can play the whole game again, defining the zeta number to be the
th solution of
sort of like how we defined the epsilons. This kind of equation, where something equals some function of itself, is called a fixed point equation.
But since we’ll have to play this game infinitely often, we might as well be more systematic about it!
The Veblen hierarchy
As you can see, we keep running into new, qualitatively different types of ordinals. First we ran into the powers of omega. Then we ran into the epsilons, and then the zetas. It’s gonna keep happening! For each type of ordinal, our notation fizzles out when we reach the first ‘fixed point’— when the xth ordinal of this type is actually equal to x.
So, instead of making up infinitely many Greek letters for different types of ordinals let’s index them… by ordinals! For each ordinal we’ll have a type of ordinal. We’ll let
be the
th ordinal of type
We can use the fixed point equation to define in terms of
In other words, we start off by defining
and then define
to be the th solution of
where we start counting at so the first solution is called the ‘zeroth’.
We can even make sense of when
itself is infinite! Suppose
is a limit of smaller ordinals. Then we define
to be the limit of
as
approaches
I’ll make this more precise next time.
We get infinitely many different types of ordinals, called the Veblen hierarchy. So, concretely, the Veblen hierarchy starts with the powers of
and then it goes on to the ‘epsilons’:
and then it goes on to what I called the ‘zetas’:
But that’s just the start!
The Feferman–Schütte ordinal
Boosting the subscript in
increases the result much more than boosting
so let’s focus on that and just let
The Veblen hierarchy contains ordinals like this:
and then ordinals like this:
and then ordinals like this:
and then this:
where of course I’m skipping huge infinite stretches of ‘boring’ ones. But note that
and
and
In short, we can plug the phi function into itself—and we get the biggest effect if we plug it into the subscript!
So, if we’re in a rush to reach some really big countable ordinals, we can try these:
But the limit of these is an ordinal that has
This is called the Feferman–Schütte ordinal and denoted
In fact, the Feferman–Schütte ordinal is the smallest solution of
Since this equation is self-referential, we can’t describe Feferman–Schütte ordinal using the Veblen hierarchy—at least, not without using the Feferman–Schütte ordinal!
Indeed, some mathematicians have made a big deal about this ordinal, claiming it’s
the smallest ordinal that cannot be described without self-reference.
This takes some explaining, and it’s somewhat controversial. After all, there’s a sense in which every fixed point equation is self-referential. But there’s a certain precise sense in which the Feferman–Schütte ordinal is different from previous ones.
Anyway, you have admit that this is a very cute description of the Fefferman–Schuette ordinal: “the smallest ordinal that cannot be described without self-reference.” Does it use self-reference? It had better—otherwise we have a contradiction!
It’s a little scary, like this picture:

More importantly for us, the Veblen hierarchy fizzles out when we hit the Feferman–Schuette ordinal. Let me say what I mean by that.
Veblen normal form
The Veblen hierarchy gives a notation for ordinals called the Veblen normal form. You can think of this as a high-powered version of Cantor normal form, which we discussed last time.
Veblen normal form relies on this result:
Theorem. Any ordinal can be written uniquely as
where is a natural number, each term is less than or equal to the previous one, and
for all
Note that we can also use this theorem to write out the ordinals and
, and so on, recursively. So, it gives us a notation for ordinals.
However, this notation is only useful when all the ordinals are less than the ordinal
that we’re trying to describe. Otherwise we need to already have a notation for
to express
in Veblen normal form!
So, the power of this notation eventually fizzles out. And the place where it does is Feferman–Schütte ordinal. Every ordinal less than this can be expressed in terms of , addition, and the function
using just finitely many symbols!
The moral
As I hope you see, the power of the human mind to see a pattern and formalize it gives the quest for large countable ordinals a strange quality. As soon as we see a systematic way to generate a sequence of larger and larger ordinals, we know this sequence has a limit that’s larger then all of those! And this opens the door to even larger ones….
So, this whole journey feels a bit like trying to outrace our car’s own shadow as we drive away from the sunset: the faster we drive, the faster it shoots ahead of us. We’ll never win.
On the other hand, we’ll only lose if we get tired.
So it’s interesting to hear what happens next. We don’t have to give up. The usual symbol for the Feferman–Schütte ordinal should be a clue. It’s called And that’s because it’s just the start of a new series of even bigger countable ordinals!
I’m dying to tell you about those. But this is enough for today.




A question that comes in mind is: can we actually find any example of an ordered set corresponding to such ordinals, OTHER than the ordinal itself? For example, a set of all natural numbers, followed by set of all pairs in lexicographic order, then all triplets, quadruplets, etc… is still just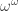 . To get to epsilon, we could imagine similar lexicographic ordering of finite sequences of finite sequences, and of finite sequences of finite sequences of finite sequences, up to arbitrarily many levels of nesting, But beyond that…
. To get to epsilon, we could imagine similar lexicographic ordering of finite sequences of finite sequences, and of finite sequences of finite sequences of finite sequences, up to arbitrarily many levels of nesting, But beyond that…
There’s an order-preserving isomorphism between the set ordinals up to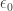 and the set of finite rooted trees, with a certain nice ordering on them. This is the basis of the hydra game, which you can play online here if you can convince your browser it’s safe to run this Java applet. (I promise: it’s safe.)
and the set of finite rooted trees, with a certain nice ordering on them. This is the basis of the hydra game, which you can play online here if you can convince your browser it’s safe to run this Java applet. (I promise: it’s safe.)
It’s also possible to explicitly describe a subset of the real line which, with the usual ordering, is isomorphic to the set of ordinals up to That’s how David Madore drew the picture here:
That’s how David Madore drew the picture here:
Click on the picture, and then click on the names of ordinals, to explore this further.
However, I don’t know if you’ll consider these structures to be different from “the ordinal itself”. Whenever two mathematical structures are isomorphic, it’s a bit subjective to decide whether they are “the same” or “different”.
I should add that the main use, so far, of countable ordinals above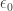 is to measure the strength of axiom systems. You can see an explanation and lots of examples here:
is to measure the strength of axiom systems. You can see an explanation and lots of examples here:
• Wikipedia, Ordinal analysis.
Proof theorists keep needing larger countable ordinals to measure the strength of stronger axiom systems! For example, it seems nobody has yet found a good notation for countable ordinals large enough to measure the strength of Zermelo—Fraenkel set theory:
• Scott Aaronson, Is there a computable ordinal encoding the proof strength of ZF? Is it knowable?, MathOverflow, 26 April 2014.
Henry Towsner’s short answer is:
Well, for the subset of real line, the question is whether each ordinal can be actually assigned a specific real number. A picture by itself isn’t much.
If you have an interval, then you can put omega in it by filling it with an infinite sequence — for <0,1), the sequence of 0, 1/2, 3/4, 7/8, etc. would be sufficient.
To get omega^2, you’d iterate this, putting another omega-worth to intervals <0,1/2), <1/2,3/4), <3/4,7/8), etc. For omega^omega, you’d fit omega into <0,1/2), omega^2 into <1/2, 3/4), omega^3 into <3/4,7/8), etc. But can the above definition of epsilon give an explicit assignment of a real (well, rational, probably) number for every ordinal below epsilon?
I actually wrote an answer to this question on Math Stack Exchange: see
http://math.stackexchange.com/questions/165151/question-of-an-isomorphism-of-epsilon-0-and-a-subset-of-the-rationals/200616#200616.
It turns out, though, that any countable ordinal can be embedded into the rationals! Given a countable ordinal , we can define a bijection
, we can define a bijection  . Start by setting
. Start by setting  . Set
. Set 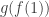 to either 1/4 or 3/4, depending on whether or not
to either 1/4 or 3/4, depending on whether or not 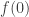 is bigger than
is bigger than 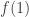 . Say it is bigger. Then set
. Say it is bigger. Then set  to be either 1/4 if it f(2) is less than f(0), 5/8 if f(2) is between f(0) and f(1), and 7/8 if f(2) is bigger than f(1). And just continue in that fashion: each time, set
to be either 1/4 if it f(2) is less than f(0), 5/8 if f(2) is between f(0) and f(1), and 7/8 if f(2) is bigger than f(1). And just continue in that fashion: each time, set 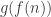 in the middle of the interval where f(n) is supposed to be (considering 0 and 1 to be -infinity and infinity). At the end you will have the ordinal
in the middle of the interval where f(n) is supposed to be (considering 0 and 1 to be -infinity and infinity). At the end you will have the ordinal  represented as a set of dyadic rationals betwen 0 and 1.
represented as a set of dyadic rationals betwen 0 and 1.
What about uncountable ordinals? Unfortunately, those cannot be embedded in the real numbers; after each ordinal, there is a next one, which must be some positive distance to the right. So if we could embed an uncountable ordinal in the real numbers, to each ordinal in the set we could associate a rational number in the interval between that ordinal and the next. But there are only countably many rational numbers, a contradiction.
Marek14 wrote:
Yes, there are various explicit ways to do this. To see one way, click on this:
and then type “CTRL-u” to see the Javascript program that drew the picture. But personally, since I don’t read Javascript very well, I’d find it more fun to make up my own way!
Oh, and here’s another way to get a well-ordered set that’s isomorphic to a fairly large ordinal.
Consider all functions
built up from the functions and
and  by addition, multiplication and exponentiation. So, functions like this:
by addition, multiplication and exponentiation. So, functions like this:
Say if
if 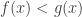 for all sufficiently large
for all sufficiently large  In 1973 Ehrenfeucht proved this ordering was a well-ordering. So, this set of functions, with this ordering, corresponds to some ordinal.
In 1973 Ehrenfeucht proved this ordering was a well-ordering. So, this set of functions, with this ordering, corresponds to some ordinal.
Which ordinal? Skolem proved that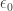 is a lower bound. In 1978, Levitz proved that
is a lower bound. In 1978, Levitz proved that 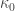 is an upper bound.
is an upper bound.
Skolem guessed that the right answer is This certainly seems like the obvious guess, given how these functions:
This certainly seems like the obvious guess, given how these functions:
look a lot like the ordinals below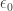 :
:
Yep, that leads to the trivial lower bound of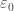 . The partial results of Levitz, Van den Dries and Dahn are (or at least include)
. The partial results of Levitz, Van den Dries and Dahn are (or at least include)  corresponds to
corresponds to 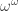 (this is very easy), and that
(this is very easy), and that 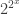 corresponds to
corresponds to 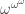 . (This is probably less easy.)
. (This is probably less easy.)
But wait, wasn’t the upper bound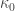 and not
and not  ?
?
Whoops, I keep forgetting to write “latex”. Is there a way to edit posts?
Alas, no. But the management usually fixes things.
Sorry, I meant Fixed.
Fixed.
I also introduced a mistake when I misunderstood the result in this paper:
• Lou van Dries and Hilbert Levitz, On Skolem’s exponential functions below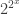 , Trans. Amer. Math. Soc. 286 (1984), 339–349.
, Trans. Amer. Math. Soc. 286 (1984), 339–349.
I’ve fixed that now.
Another very nice well-ordered set are the “Fusible numbers”. See here: http://www.mathpuzzle.com/fusible.pdf for a very nice presentation of the fusible numbers, although a couple of things in the slides are incorrect.
Basically, the idea is that you have an infinite set of fuses that each take 1 hour to burn, and the fusible numbers are those numbers of hours that you can time by burning the fuses in various ways. So you can time 1/2 hour by light a single fuse at one end. You can time 3/4 of an by lighting fuse 1 at both ends and fuse 2 at one end at time 0, and lighting the other end of fuse 2 when fuse 1 burns out.
Mathematically the fusible numbers are defined as the smallest set which contains 0 and is closed under the operation provided that
provided that 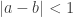 . This correpsonds to lighting one end of a fuse at time a and the other at time b, so it will burn out at time
. This correpsonds to lighting one end of a fuse at time a and the other at time b, so it will burn out at time 
A relatively simple argument proves that the fusible numbers are well-ordered, so again we can ask what ordinal the fusible numbers correspond to. We can identify a subset of the fusible numbers with order type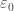 , so that is a lower bound for the order type of the entire set. It is conjectured that the order type is exactly
, so that is a lower bound for the order type of the entire set. It is conjectured that the order type is exactly 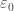 , but we don’t know for sure; so the situation is much like the situation for the problem of Skolem.
, but we don’t know for sure; so the situation is much like the situation for the problem of Skolem.
Another interesting fact about fusible numbers: If we define as the next fusible number after x, and
as the next fusible number after x, and 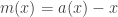 , then m(x) will be a power of 1/2 (when x is a fusible number). So if we let
, then m(x) will be a power of 1/2 (when x is a fusible number). So if we let  and focus on when x is a natural number, f(x) will be a very fast-growing function of x. If a conjecture by Junyan Xu for the fusible numbers is true, then the fusible numbers will have order type
and focus on when x is a natural number, f(x) will be a very fast-growing function of x. If a conjecture by Junyan Xu for the fusible numbers is true, then the fusible numbers will have order type 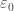 and it appears that f will grow at the rate close to
and it appears that f will grow at the rate close to  , where F is the fast-growing hierarchy. This is a very fast-growing function;
, where F is the fast-growing hierarchy. This is a very fast-growing function; 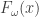 already grows a rate equal to the Ackermann function!
already grows a rate equal to the Ackermann function!
If Xu’s conjecture is false, then the order type of the fusible numbers could be larger, and the function f could grow even faster.
Cool! It’s always fun to see very fast-growing functions “in nature”.
Here are some puzzles in ordinal arithmetic. If you’re a super-expert, maybe you should let other people try them:
Puzzle 1. What is ?
?
Puzzle 2. What is ?
?
Puzzle 3. What is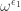 ?
?
Puzzle 4. What is ?
?
Puzzle 5. What is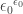 ?
?
Puzzle 6. What is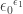 ?
?
Puzzle 7. What is ?
?
Puzzle 8. What is ?
?
Well, let’s see…
1 and 3 are trivial. Epsilons are fixed points of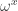 , so
, so 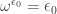 and
and  .
.
2 and 4: is
is 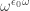 , or
, or  , similarly
, similarly  is
is  .
.
5 and 8: Similarly, we get that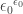 is
is  , or
, or  and
and  is
is 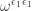 , or
, or 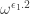 .
.
6: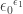 is is
is is 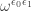 , or
, or  – but
– but 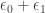 is simply
is simply  , so it’s
, so it’s  , or simply
, or simply  .
.
7: Through analogical construction, we get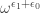 . We can’t simplify
. We can’t simplify  any further, so we probably can’t get a more succinct representation.
any further, so we probably can’t get a more succinct representation.
2, 4, 5, 7, and 8 aren’t quite right, unless you switch at some point from talking about the ordinal to talking about the exponent.
Yeah, that was incorrect.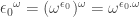 . If
. If 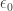 is an exponential tower of
is an exponential tower of 
 ‘s, then this is a tower of
‘s, then this is a tower of 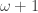
 ‘s. So, for 4, we get
‘s. So, for 4, we get
for 5 we get
for 8
and for 7
I made a mistake in 6 as well, but the final result should still stay since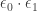 should still equal
should still equal 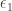 .
.
Correct, but those are not in (iterated) Cantor Normal Form; you have to keep going until you everything is either addition or exponentiation with base .
.
Not sure how to do that — after all, they all involve epsilons; aren’t Cantor Normal forms of epsilons already infinite? I could iterate it like that, but I’m not sure how to write the result; never used LaTeX before today, though it’s similar to equation tools in some text editors I used when translating books in the past.
Indeed, the epsilon numbers cannot be reduced, so you just leave them as they are. However, numbers like are not epsilon numbers, so they should be reduced (in this case to
are not epsilon numbers, so they should be reduced (in this case to 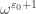 ).
).
I described Cantor normal form last time:
This works for every ordinal, but if you apply it to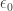 you get
you get
which isn’t very helpful. So, we can agree to leave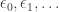 alone instead of applying this theorem to them. However, the theorem says we can always take expressions like
alone instead of applying this theorem to them. However, the theorem says we can always take expressions like
or
and rewrite them using the theorem.
Of course the proof of the theorem is more informative than the mere statement of the theorem, since it says how to rewrite these expressions!
OK, so if we use normal form with epsilons, we have:
Puzzle 1.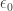
Puzzle 2.
Puzzle 3.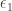
Puzzle 4.
Puzzle 5.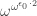
Puzzle 6.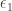
Puzzle 7.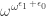
Puzzle 8.
Correct!
Hi – I’d like to give it a shot.
So firstly, when counting up with ordinals, I find it handy to avoid forms like and instead to think of everything in powers of
and instead to think of everything in powers of 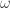 unless at a fixed point of
unless at a fixed point of 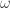 (i.e., a pure epsilon number).
(i.e., a pure epsilon number).
So that means when getting up through the ordinals ,
,  , …, I would stop at
, …, I would stop at 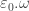 and instead express that as
and instead express that as 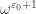 , because it is the next power of
, because it is the next power of 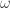 after the first fixed point,
after the first fixed point,  . Just feels a bit tidier to me.
. Just feels a bit tidier to me.
So that being said, I’d express those 8 expressions as powers of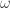 unless they are epsilon numbers. My answers are as follows:
unless they are epsilon numbers. My answers are as follows:
1)

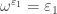

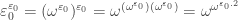

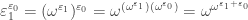

2)
3)
4)
5)
6)
7)
8)
Hope that all renders properly!
Ah! A touch too late :)
It’s never too late! When two people independently get the same answer, it increases the spectators’ confidence that the answer is right.
Now, you have written that is the limit of the sequence
is the limit of the sequence
So, what is, say, limit of this similar sequence:
Should it be greater than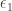 , but probably smaller than
, but probably smaller than  ?
?
Second question: all the limit ordinals constructed so far are supremas of some infinite sequences, i.e. sequences with members. Are there countable ordinals that require longer sequences? Or can all ordinals below
members. Are there countable ordinals that require longer sequences? Or can all ordinals below 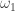 (the first uncountable ordinal, which of course cannot be expressed in countable terms) be expressed using sequences with
(the first uncountable ordinal, which of course cannot be expressed in countable terms) be expressed using sequences with  members?
members?
Hi Marek – my instinct would be that the sequence you reference would still only indicate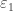 , but I’ll leave it to the experts to explain/confirm. Interestingly,
, but I’ll leave it to the experts to explain/confirm. Interestingly, 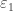 can also be represented by an infinite tower of
can also be represented by an infinite tower of  . One thing I find fascinating is the surreal number system, which gives meaning to forms like
. One thing I find fascinating is the surreal number system, which gives meaning to forms like  and
and  . But that’s a huge topic in itself! I’d recommend Gonshor’s Introduction to the Theory of Surreal Numbers if you’d like to learn more.
. But that’s a huge topic in itself! I’d recommend Gonshor’s Introduction to the Theory of Surreal Numbers if you’d like to learn more.
Oh, I’m familiar with those. Some people admired actors or singers in their teens; my idol was Conway, ever since I found a copy of Winning Ways in a local university library.
Marek14 wrote:
This is a good puzzle. I’ll just give a small hint.
Let’s call the limit of this sequence It’s pretty easy to see that
It’s pretty easy to see that
So, by definition, is an epsilon number. If it’s the
is an epsilon number. If it’s the  th epsilon number, we call it
th epsilon number, we call it 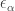 .
.
So, it can’t be greater than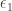 and smaller than
and smaller than 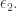 There are no epsilon numbers between these two!
There are no epsilon numbers between these two!
On the other hand, is certainly greater than or equal to
is certainly greater than or equal to 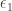 , which is the limit of
, which is the limit of
After all, each term in the sequence you gave is greater than or equal to the corresponding term in this sequence.
So, is either
is either 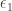 ,
,  , or
, or 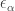 for some
for some  .
.
At this point I will shut up and let others continue.
If we call the first sequence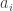 and the second sequence
and the second sequence  , notice that
, notice that
So it should be clear that any ordinal larger than all of the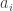 will also be larger than all of the
will also be larger than all of the  and vice versa, so of course the smallest such ordinal will be the same for both.
and vice versa, so of course the smallest such ordinal will be the same for both.
Remember that an ordinal is countably infinite if and only if there is a bijection f from the natural numbers to
is countably infinite if and only if there is a bijection f from the natural numbers to  . So if
. So if  is limit, we can form a sequence of length
is limit, we can form a sequence of length  by starting with f(0), then selecting the first f(n) that is greater than it, then the next greater ordinal, and so on. This is obviously a sequence of length
by starting with f(0), then selecting the first f(n) that is greater than it, then the next greater ordinal, and so on. This is obviously a sequence of length  , and it will have limit
, and it will have limit  , since for any ordinal
, since for any ordinal  , we will at some point pass
, we will at some point pass  in the sequence, at which point we will either select
in the sequence, at which point we will either select  , or pass it by because we have already exceeded it.
, or pass it by because we have already exceeded it.
Your description of the Veblen normal form is a bit confused, it mixes alpha and beta.
Thanks, I’ll check that out and fix if it needed.
I don’t see a mistake here:
The paragraphs after that refer to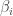 as
as 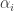 (and to
(and to  as
as 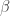 )
)
Got it! Thanks. Fixed.
By the way, Wikipedia says that in Veblen normal form we have
but I’m afraid we might only have
when reaches or exceeds the small Veblen ordinal, which is a fixed point of all the functions
reaches or exceeds the small Veblen ordinal, which is a fixed point of all the functions 
What’s the Veblen normal form of the small Veblen ordinal? I feel I only understand Veblen normal form for ordinals below this.
We can always have , by choosing
, by choosing 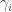 to be as large as possible. (We can choose a maximal
to be as large as possible. (We can choose a maximal 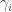 since the set of possible values is closed; but if
since the set of possible values is closed; but if  then we can increase
then we can increase 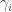 by one.)
by one.)
The Veblen normal form for any strongly critical ordinal $\latex \alpha$ such as the Small Veblen Ordinal is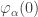 .
.
Thanks! Now I feel dumb, because I should have been able to figure that out. But that’s very helpful and reassuring.
Wow. You really made this one roll, John. I have to admit, I thought about collecting stuff for a book as well, but reading this post I might end up preferring to suggest yours. Fancy! And no, that wouldn’t stop me.
Thanks! It was your post on the Feferman–Schütte ordinal that revived my interest in explaining these ordinals:
https://plus.google.com/+RefurioAnachro/posts/KNabqFVa8SM
(It’s cool how a G+ post automatically shows up here; I’d never tried that trick before.)
Near the end you say that every ordinal less than the Feferman-Schutte ordinal can be expressed in terms of , and the
, and the 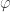 function. The 1 should be replaced by 0 I think.
function. The 1 should be replaced by 0 I think.
Also, I think ordinal neophytes will be at a loss on how to get things like and
and  ; perhaps you could add some detail there?
; perhaps you could add some detail there?
Royce wrote:
You’re right!
Hmm, I don’t want to turn this road trip into a textbook… and the advantage of blog articles is that people can ask questions… but I’ll mention that is the first ordinal bigger than
is the first ordinal bigger than 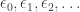
Next time I’ll talk about some of this stuff a bit more formally.
Well, maybe it would be easier to say that ?
?
That might be more concise, but perhaps more confusing to the uninitiated. (I think it’s less clear that the ordinal defined by that expression is closed under omega exponentiation, for example.)
If I said
someone might point out that I haven’t defined an infinite sum of ordinals, or even pointed to a definition.
Of course the definition of this infinite sum is that it’s the limit of
but that seems more complicated than saying is the limit of
is the limit of
Last time we saw how to name a lot of countable ordinals using an idea developed by Veblen. In fact, all ordinals less than the ‘Feferman–Schütte ordinal’. This time I’ll explain Veblen’s idea more precisely and go even further, still using Veblen’s work.
Getting back to the Paris-Harrington theorem: the original proof used non-standard models of PA. (Kanamori and McAloon soon simplified it; the treatment in the recent book by Katz and Reimann is particularly easy to follow.) That’s the one I want to look at here.
But since you had such fun with ordinals here (and here and here), I better add that Ketonen and Solovay later gave a proof based on the ε0 stuff and the hierarchy of fast-growing functions. (The variation due to Loebl and Nešetřil is nice and short.) We should talk about this sometime! I wish I understood all the connections better. (Stillwell’s Roads to Infinity offers a nice entry point, though he does like to gloss over details.)