Struggles with the Continuum (Part 6)

Last time I sketched how physicists use quantum electrodynamics, or ‘QED’, to compute answers to physics problems as power series in the fine structure constant, which is

\displaystyle{ \alpha = \frac{1}{4 \pi \epsilon_0} \frac{e^2}{\hbar c} \approx \frac{1}{137.036} }

I concluded with a famous example: the magnetic moment of the electron. With a truly heroic computation, physicists have used QED to compute this quantity up to order \alpha^5. If we also take other Standard Model effects into account we get agreement to roughly one part in 10^{12}.

However, if we continue adding up terms in this power series, there is no guarantee that the answer converges. Indeed, in 1952 Freeman Dyson gave a heuristic argument that makes physicists expect that the series diverges, along with most other power series in QED!

The argument goes as follows. If these power series converged for small positive \alpha, they would have a nonzero radius of convergence, so they would also converge for small negative \alpha. Thus, QED would make sense for small negative values of \alpha, which correspond to imaginary values of the electron’s charge. If the electron had an imaginary charge, electrons would attract each other electrostatically, since the usual repulsive force between them is proportional to e^2. Thus, if the power series converged, we would have a theory like QED for electrons that attract rather than repel each other.

However, there is a good reason to believe that QED cannot make sense for electrons that attract. The reason is that it describes a world where the vacuum is unstable. That is, there would be states with arbitrarily large negative energy containing many electrons and positrons. Thus, we expect that the vacuum could spontaneously turn into electrons and positrons together with photons (to conserve energy). Of course, this not a rigorous proof that the power series in QED diverge: just an argument that it would be strange if they did not.

To see why electrons that attract could have arbitrarily large negative energy, consider a state \psi with a large number N of such electrons inside a ball of radius R. We require that these electrons have small momenta, so that nonrelativistic quantum mechanics gives a good approximation to the situation. Since its momentum is small, the kinetic energy of each electron is a small fraction of its rest energy m_e c^2. If we let \langle \psi, E \psi\rangle be the expected value of the total rest energy and kinetic energy of all the electrons, it follows that \langle \psi, E\psi \rangle is approximately proportional to N.

The Pauli exclusion principle puts a limit on how many electrons with momentum below some bound can fit inside a ball of radius R. This number is asymptotically proportional to the volume of the ball. Thus, we can assume N is approximately proportional to R^3. It follows that \langle \psi, E \psi \rangle is approximately proportional to R^3.

There is also the negative potential energy to consider. Let V be the operator for potential energy. Since we have N electrons attracted by an 1/r potential, and each pair contributes to the potential energy, we see that \langle \psi , V \psi \rangle is approximately proportional to -N^2 R^{-1}, or -R^5. Since R^5 grows faster than R^3, we can make the expected energy \langle \psi, (E + V) \psi \rangle arbitrarily large and negative as N,R \to \infty.

Note the interesting contrast between this result and some previous ones we have seen. In Newtonian mechanics, the energy of particles attracting each other with a 1/r potential is unbounded below. In quantum mechanics, thanks the uncertainty principle, the energy is bounded below for any fixed number of particles. However, quantum field theory allows for the creation of particles, and this changes everything! Dyson’s disaster arises because the vacuum can turn into a state with arbitrarily large numbers of electrons and positrons. This disaster only occurs in an imaginary world where \alpha is negative—but it may be enough to prevent the power series in QED from having a nonzero radius of convergence.

We are left with a puzzle: how can perturbative QED work so well in practice, if the power series in QED diverge?

Much is known about this puzzle. There is an extensive theory of ‘Borel summation’, which allows one to extract well-defined answers from certain divergent power series. For example, consider a particle of mass m on a line in a potential

V(x) = x^2 + \beta x^4

When \beta \ge 0 this potential is bounded below, but when \beta < 0 it is not: classically, it describes a particle that can shoot to infinity in a finite time. Let H = K + V be the quantum Hamiltonian for this particle, where K is the usual operator for the kinetic energy and V is the operator for potential energy. When \beta \ge 0, the Hamiltonian H is essentially self-adjoint on the set of smooth wavefunctions that vanish outside a bounded interval. This means that the theory makes sense. Moreover, in this case H has a ‘ground state’: a state \psi whose expected energy \langle \psi, H \psi \rangle is as low as possible. Call this expected energy E(\beta). One can show that E(\beta) depends smoothly on \beta for \beta \ge 0, and one can write down a Taylor series for E(\beta).

On the other hand, when \beta < 0 the Hamiltonian H is not essentially self-adjoint. This means that the quantum mechanics of a particle in this potential is ill-behaved when \beta < 0. Heuristically speaking, the problem is that such a particle could tunnel through the barrier given by the local maxima of V(x) and shoot off to infinity in a finite time.

This situation is similar to Dyson’s disaster, since we have a theory that is well-behaved for \beta \ge 0 and ill-behaved for \beta < 0. As before, the bad behavior seems to arise from our ability to convert an infinite amount of potential energy into other forms of energy. However, in this simpler situation one can prove that the Taylor series for E(\beta) does not converge. Barry Simon did this around 1969. Moreover, one can prove that Borel summation, applied to this Taylor series, gives the correct value of E(\beta) for \beta \ge 0. The same is known to be true for certain quantum field theories. Analyzing these examples, one can see why summing the first few terms of a power series can give a good approximation to the correct answer even though the series diverges. The terms in the series get smaller and smaller for a while, but eventually they become huge.

Unfortunately, nobody has been able to carry out this kind of analysis for quantum electrodynamics. In fact, the current conventional wisdom is that this theory is inconsistent, due to problems at very short distance scales. In our discussion so far, we summed over Feynman diagrams with \le n vertices to get the first n terms of power series for answers to physical questions. However, one can also sum over all diagrams with \le n loops. This more sophisticated approach to renormalization, which sums over infinitely many diagrams, may dig a bit deeper into the problems faced by quantum field theories.

If we use this alternate approach for QED we find something surprising. Recall that in renormalization we impose a momentum cutoff \Lambda, essentially ignoring waves of wavelength less than \hbar/\Lambda, and use this to work out a relation between the the electron’s bare charge e_\mathrm{bare}(\Lambda) and its renormalized charge e_\mathrm{ren}. We try to choose e_\mathrm{bare}(\Lambda) that makes e_\mathrm{ren} equal to the electron’s experimentally observed charge e. If we sum over Feynman diagrams with \le n vertices this is always possible. But if we sum over Feynman diagrams with at most one loop, it ceases to be possible when \Lambda reaches a certain very large value, namely

\displaystyle{ \Lambda \; = \; \exp\left(\frac{3 \pi}{2 \alpha} + \frac{5}{6}\right) m_e c \; \approx \; e^{647} m_e c}

According to this one-loop calculation, the electron’s bare charge becomes infinite at this point! This value of \Lambda is known as a ‘Landau pole’, since it was first noticed in about 1954 by Lev Landau and his colleagues.

What is the meaning of the Landau pole? We said that poetically speaking, the bare charge of the electron is the charge we would see if we could strip off the electron’s virtual particle cloud. A somewhat more precise statement is that e_\mathrm{bare}(\Lambda) is the charge we would see if we collided two electrons head-on with a momentum on the order of \Lambda. In this collision, there is a good chance that the electrons would come within a distance of \hbar/\Lambda from each other. The larger \Lambda is, the smaller this distance is, and the more we penetrate past the effects of the virtual particle cloud, whose polarization ‘shields’ the electron’s charge. Thus, the larger \Lambda is, the larger e_\mathrm{bare}(\Lambda) becomes.

So far, all this makes good sense: physicists have done experiments to actually measure this effect. The problem is that according to a one-loop calculation, e_\mathrm{bare}(\Lambda) becomes infinite when \Lambda reaches a certain huge value.

Of course, summing only over diagrams with at most one loop is not definitive. Physicists have repeated the calculation summing over diagrams with \le 2 loops, and again found a Landau pole. But again, this is not definitive. Nobody knows what will happen as we consider diagrams with more and more loops. Moreover, the distance \hbar/\Lambda corresponding to the Landau pole is absurdly small! For the one-loop calculation quoted above, this distance is about

\displaystyle{ e^{-647} \frac{\hbar}{m_e c} \; \approx \; 6 \cdot 10^{-294}\, \mathrm{meters} }

This is hundreds of orders of magnitude smaller than the length scales physicists have explored so far. Currently the Large Hadron Collider can probe energies up to about 10 TeV, and thus distances down to about 2 \cdot 10^{-20} meters, or about 0.00002 times the radius of a proton. Quantum field theory seems to be holding up very well so far, but no reasonable physicist would be willing to extrapolate this success down to 6 \cdot 10^{-294} meters, and few seem upset at problems that manifest themselves only at such a short distance scale.

Indeed, attitudes on renormalization have changed significantly since 1948, when Feynman, Schwinger and Tomonoga developed it for QED. At first it seemed a bit like a trick. Later, as the success of renormalization became ever more thoroughly confirmed, it became accepted. However, some of the most thoughtful physicists remained worried. In 1975, Dirac said:

Most physicists are very satisfied with the situation. They say: ‘Quantum electrodynamics is a good theory and we do not have to worry about it any more.’ I must say that I am very dissatisfied with the situation, because this so-called ‘good theory’ does involve neglecting infinities which appear in its equations, neglecting them in an arbitrary way. This is just not sensible mathematics. Sensible mathematics involves neglecting a quantity when it is small—not neglecting it just because it is infinitely great and you do not want it!

As late as 1985, Feynman wrote:

The shell game that we play [. . .] is technically called ‘renormalization’. But no matter how clever the word, it is still what I would call a dippy process! Having to resort to such hocus-pocus has prevented us from proving that the theory of quantum electrodynamics is mathematically self-consistent. It’s surprising that the theory still hasn’t been proved self-consistent one way or the other by now; I suspect that renormalization is not mathematically legitimate.

By now renormalization is thoroughly accepted among physicists. The key move was a change of attitude emphasized by Kenneth Wilson in the 1970s. Instead of treating quantum field theory as the correct description of physics at arbitrarily large energy-momenta, we can assume it is only an approximation. For renormalizable theories, one can argue that even if quantum field theory is inaccurate at large energy-momenta, the corrections become negligible at smaller, experimentally accessible energy-momenta. If so, instead of seeking to take the \Lambda \to \infty limit, we can use renormalization to relate bare quantities at some large but finite value of \Lambda to experimentally observed quantities.

From this practical-minded viewpoint, the possibility of a Landau pole in QED is less important than the behavior of the Standard Model. Physicists believe that the Standard Model would suffer from Landau pole at momenta low enough to cause serious problems if the Higgs boson were considerably more massive than it actually is. Thus, they were relieved when the Higgs was discovered at the Large Hadron Collider with a mass of about 125 GeV/c2. However, the Standard Model may still suffer from a Landau pole at high momenta, as well as an instability of the vacuum.

Regardless of practicalities, for the mathematical physicist, the question of whether or not QED and the Standard Model can be made into well-defined mathematical structures that obey the axioms of quantum field theory remain open problems of great interest. Most physicists believe that this can be done for pure Yang–Mills theory, but actually proving this is the first step towards winning $1,000,000 from the Clay Mathematics Institute.

• Part 1: introduction; the classical mechanics of gravitating point particles.

• Part 2: the quantum mechanics of point particles.

• Part 3: classical point particles interacting with the electromagnetic field.

• Part 4: quantum electrodynamics.

• Part 5: renormalization in quantum electrodynamics.

• Part 6: summing the power series in quantum electrodynamics.

• Part 7: singularities in general relativity.

• Part 8: cosmic censorship in general relativity; conclusions.

This entry was posted on Wednesday, September 21st, 2016 at 1:00 am and is filed under mathematics, physics. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.

21 Responses to Struggles with the Continuum (Part 6)

  1. rtheo says:
    21 September, 2016 at 9:15 am

    This whole story is somehow reminiscent of a well known historical accident: Epicycles! Then again, an ellipse was just a deformation of a circle, avoided for centuries only due to philosophical preoccupations. Maybe one should also try that to be sure no possibility has been left unchecked by tracing backwards the source of the infinities as errors of a fitting process (interpretation problems aside).

    Reply
    • John Baez says:
      21 September, 2016 at 2:08 pm

      Digressing a bit, it’s interesting to note that Copernicus’ heliocentric theory of the solar system had more epicycles than Ptolemy’s geocentric system, and didn’t fit the data better. It was only when Kepler went ahead with the heliocentric theory and introduced ellipses that the epicycles went away.

      I’m not sure what this means for the problem with infinities in physics. If anything, perhaps it means you need to try a theory that seems worse in some ways before you reach a theory that’s better.

      Reply
  2. Martin Gisser says:
    21 September, 2016 at 1:20 pm

    Thanks a lot, John! With stuff like this you kept my philosophical math/phys flame burning over many many years meanwhile…

    What about the connection of renormalization to numerical integration methods, i.e. the Butcher group? Could a perspective from this side help resolve the continuum problems?

    Reply
    • John Baez says:
      21 September, 2016 at 2:17 pm

      I’m completely forgetting what little I once knew about the connection of renormalization to numerical integration methods. So I’ll just say this. I’m happy that starting in the 1990’s, more mathematicians started taking renormalization seriously and tried to understand it more conceptually and make its mechanics more beautiful. The most famous example is the work of Connes and Kreimer, which has launched a huge line of research connecting renormalization to Hopf algebras and combinatorics. We may need four or five more revolutionary ideas to make quantum field theory rigorous. But the idea of taking what physicists have already done and trying to make it clearer and more beautiful is a promising strategy that doesn’t require magical strokes of genius.

      Reply
    • Martin Gisser says:
      21 September, 2016 at 11:29 pm

      My hunch (armchair scientist hallucination) was sort of a discretized abstract QFT from a computer numerics observer/ables perspective. Concrete QFT would then appear as a projective limit.

      So, it looks Connes-Kreimer “stuff” (Hopf algebras etc.) has shed mathematical light on renormalization, but hasn’t helped much yet in a mathematical understanding of QFT as a whole?

      Hopf algebras meanwhile pop up all over the place. Even in very basic things, e.g. last year I rediscovered the shuffle Hopf algebra in tensor calculus Leibniz’ formulas for higher covariant derivatives (I have a variant where the antipode map appears, but no serious use yet). That’s why I recalled the existence of the Connes-Kreimer paper – of which methinks I first heard/read from you :-)

      Reply
      • John Baez says:
        21 September, 2016 at 11:37 pm

        Martin wrote:

        So, it looks Connes-Kreimer “stuff” (Hopf algebras etc.) has shed mathematical light on renormalization, but hasn’t helped much yet in a mathematical understanding of QFT as a whole?

        That seems a bit unfair. Renormalization is a crucial part of QFT “as a whole”.

        Reply
      • Martin Gisser says:
        22 September, 2016 at 1:21 am

        Yeah, sorry for that. And maybe I should have googled a bit more before posting stupid comments. (But my brain clockwork often runs backwards and you almost made it explode once again, for I haven’t cared much about QFT in the last 2 decades. And I’m actually on the run, bad timing…)

        Now I found the following Hopf algebra gem, which I might even find digestible. It might be a point of entry for my “hunch” – and, lo and behold, the toy model has a continuum problem…

        • Christian Brouder, Quantum field theory meets Hopf algebra, https://arxiv.org/abs/hep-th/0611153

        Reply
        • John Baez says:
          22 September, 2016 at 2:40 am

          In real life gems are rarely digestible, but in mathematics they can be! This does look appealing: perhaps it’s an introduction to quantum field theory for people who already like Hopf algebras. This is the kind of thing that only became imaginable after the work of Connes and Kreimer… and it’s worth looking for more such things, because their original paper was really just opening the door to a roomful of treasure.

        • Gisser Martin says:
          22 September, 2016 at 12:13 pm

          Yeah, it looks frighteningly appealing. At least it allows me a more concrete formulation of my hunch: In 2.1 loc. cit. a coalgebra C is defined with a finite number of spacetime points. Maybe one can plug in some finite difference scheme here. This amounts perhaps to some 3rd quantization (tensor algebra of a tensor algebra of a tensor algebra, in a more manageable Hopf algebra sense). But I bet some better minds than me have already thought of this…

          Now I’m off to the wilderness, hopefully to forget about this brainstorm :-) (Google+ login didn’t work)

        • Martin Gisser says:
          26 September, 2016 at 9:23 pm

          Back from the wilderness for a day. Need to report: O small sweet planet! While I managed to forget about Hopf algebra, instead I got a total recall of the early days of the Azimuth project! Because on that sunny meadow in the nowhere of Barvaria with a bunch of merry hippies I met Curtis F himself! Alas right then I had to leave…

  3. FiftyForty says:
    21 September, 2016 at 10:15 pm

    The ‘Last time’ hyperlink seems to be broken.

    Reply
  4. domenico says:
    22 September, 2016 at 2:58 pm

    I have a problem, in an Universe with two only charges particles electron-positron and in another Universe with only two bodies with the same masses (and temperature bodies near the absolute zero or objects like black holes with the right masses) the collisions could have the same cross sections and the same trajectories (with the right masses and with some right great distance, obtaining an indinstinguishability of the forces effects and indistinguishability of particles dynamics).
    If I use the Quantum Electrodynamic to evaluate dynamic of the particles, then could the gravitational effects be calculated using the Quantum Electrodynamic? If it is all true for macroscopic object, it could be true for quantum objects? Or is this too simple?

    Reply
    • rtheo says:
      22 September, 2016 at 4:00 pm

      A possible problem with such a direct correspondence would be the “background” character of the gravitational “field” -which is no more an ordinary field but a metric- and it’s self interacting nature. How does one maps results of a linear theory to those of a non-linear one? On the other hand an interesting assumption perhaps would be to take the particle internal mass densities ~ e^2*f(r) -with f supposedly falling sufficiently fast- in order to geometrize the total equations of motion (by eliminating the charge/mass ratio for both massive and charged particles) and try to fit for the unkown f(r) from empirical data. Would it turn out to be singular? Just a thought…

      Reply
    • John Baez says:
      22 September, 2016 at 8:01 pm

      In reality, gravity obeys nonlinear equations (the Einstein equations) that are rather different from the linear equations described by the electromagnetic field (Maxwell’s equations). So, QED is not a good theory of quantum gravity.

      We can linearize Einstein gravity, quantize that, and get a theory of massless spin-2 particles: gravitons. These still behave differently than the massless spin-1 particles in QED, namely photons.

      By the way, the fact that photons have odd spin while gravitons have even spin can be seen as the reason why like charges repel while like masses attract!

      (We can try to make like charges attract by taking the fine structure constant to be negative, but as explained this gives a very nasty theory, which is still not quantum gravity.)

      Still, there are interesting parallels between gravity and electromagnetism. In particular, we can take Einstein’s theory of gravity, linearize it, and then chop the gravitational field into ‘gravitoelectric’ and ‘gravitomagnetic’ parts, that are somewhat analogous to the electric and magnetic field. These fields obey equations that look a bit like Maxwell’s equations! Check it out:

      • Gravitoelectromagnetic field equations, Wikipedia.

      However, be careful: the talk page shows that the Wikipedia editors are pretty confused about what precise assumptions are used to derive the gravitoelectromagnetic field equations from general relativity! Certainly you need to linearize about a flat solution, but you may also need more.

      I think this book would help clarify things:

      • Ignazio Ciufolini and John Archibald Wheeler, Gravitation and Inertia, Princeton U. Press, Princeton, 1995.

      Reply
      • Todd Trimble says:
        22 September, 2016 at 9:53 pm

        “By the way, the fact that photons have odd spin while gravitons have even spin can be seen as the reason why like charges repel while like masses attract!”

        Could you explain this a bit more?

        Reply
      • John Baez says:
        22 September, 2016 at 11:06 pm

        Todd wrote:

        Could you explain this a bit more?

        Unfortunately I don’t have an intuitive understanding of why this is true: for me it’s just a calculation that I’ve watched people do.

        You can see the calculation here:

        • Warren Siegel, Fields, page 184.

        However, it may be better to start with this puzzle: “How can virtual particles be responsible for attractive forces in the first place?” There’s a nice discussion of that here:

        • Matt McIrvin, Some frequently asked questions about virtual particles, Physics FAQ.

        He starts as follows:

        The most obvious problem with a simple, classical picture of virtual particles is that this sort of behavior can’t possibly result in attractive forces. If I throw a ball at you, the recoil pushes me back; when you catch the ball, you are pushed away from me. How can this attract us to each other? The answer lies in Heisenberg’s uncertainty principle.

        Suppose that we are trying to calculate the probability (or, actually, the probability amplitude) that some amount of momentum, p, gets transferred between a couple of particles that are fairly well- localized. The uncertainty principle says that definite momentum is associated with a huge uncertainty in position. A virtual particle with momentum p corresponds to a plane wave filling all of space, with no definite position at all. It doesn’t matter which way the momentum points; that just determines how the wavefronts are oriented. Since the wave is everywhere, the photon can be created by one particle and absorbed by the other, no matter where they are. If the momentum transferred by the wave points in the direction from the receiving particle to the emitting one, the effect is that of an attractive force.

        The moral is that the lines in a Feynman diagram are not to be interpreted literally as the paths of classical particles. Usually, in fact, this interpretation applies to an even lesser extent than in my example, since in most Feynman diagrams the incoming and outgoing particles are not very well localized; they’re supposed to be plane waves too.

        The uncertainty principle opens up the possibility that a virtual photon could impart a momentum that corresponds to an attractive force as well as to a repulsive one. But you may well ask what makes the force repulsive for like charges and attractive for opposite charges! Does the virtual photon know what kind of particle it’s going to hit?

        It’s hard even for particle physicists to see this using the Feynman diagram rules of QED, because they’re usually formulated in a manner designed to answer a completely different question: that of the probability of particles in plane-wave states scattering off of each other at various angles. Here, though, we want to understand what nudges a couple of particles that are just sitting around some distance apart—to explain the experiment you may have done in high school, in which charged balls of aluminum foil repel each other when hanging from strings. We want to do this using virtual particles. It can be done.

        And then he does it. He does it using lots of simplifying approximations that might be disturbing if one isn’t used to computing these things. But those are all okay. The unfortunate part is this: he doesn’t highlight the role of the photon’s spin. So, you can’t read his argument and see what would change if that spin were even rather than odd.

        However, if you read Matt’s story you’ll see that in the end, it all depends on some constructive and/or destructive interference, which in turn depends on some signs. So, you can probably at least imagine that if we changed the spin of the virtual particle from odd to even, some signs would change and we’d get a force where ‘like charges attract’ (namely gravity, with ‘charges’ being masses), rather than one where like charges repel.

        If you take Matt’s essay, and Warren Siegel’s calculation, and look at them together for a long time, some intuitive explanation should emerge. But I haven’t done this yet. Siegel tends to do calculations very rapidly, which is why his book is only 885 pages long. So, the crucial factor of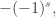 -(-1)^s, where s is the spin of the particle carrying the force, seems to pop out as if by magic!

        Feynman would be able to give a nice verbal explanation.

        Reply
        • Todd Trimble says:
          22 September, 2016 at 11:58 pm

          Well, it sounds very interesting! (And a challenge for teachers like you or Feynman who strive for intuitive explanations.)

          As a mathematician used to thinking of the word “odd” (in the context of spin) as referring to odd-degree components of super-representations, I was at first confused: photons are bosons, where the relevant representations live in even-degree parts, right? But then I thought, no wait, John knows this stuff backwards and forwards, he’d never get mixed up about anything like that. I.e., you really did mean odd spin (as in odd integer, not some half-integer)! And then realized I had no idea what to make of the assertion!

          There is a kind of lame intuition I have that “bosons attract, fermions repel” in the sense that e.g. two electrons as fermions cannot occupy the same state. I wonder if there’s some twisted way in which a similar idea is at work here… but maybe I should try first to read these references.

        • John Baez says:
          23 September, 2016 at 12:53 am

          The way bosons like to congregate in Bose-Einstein condensates while fermions standoffishly obey the Pauli exclusion principle is, I believe, a completely separate issue. Force carriers are bosons, so they all have integer spin, and the issue of whether like charges attract or repel depends on whether that integer is even or odd.

          I forgot to mention another classic example: the Yukawa theory! In this theory spin-1/2 particles interact by exchanging a spin-0 particle. This was the very first theory of the strong nuclear force: Yukawa had protons and neutrons interact by exchanging a massive spin-0 “meson”. This force would be attractive, so it could hold nuclei together.

          Yukawa proposed his theory in 1935. In 1936 experimenters looking at cosmic rays found a particle of roughly the right mass! Hurrah! But it turned out to be a spin-1/2 particle that didn’t interact strongly at all, prompting I. I. Rabi’s famous quip: “Who ordered that?”

          This was the muon, the first of the ‘second generation’ of particles. The existence of three generations is still a total mystery.

          Considerably later, in 1947, they found the pion, which fits the bill quite nicely. And Yukawa won the Nobel prize.

          They originally called the muon the ‘mu meson’, due to this mixup, but now we say it’s not a meson at all.

          The theory of protons and neutrons attracting by exchanging spin-0 pions is still a reasonable approximation in some situations, for example in nuclei and certain layers of a neutron star. And Heisenberg’s development of this theory led to the introduction of ‘isospin SU(2)’, which eventually led Yang and Mills to ‘SU(2) gauge theory’ and the Yang–Mills equations. For example, there are really three pions—positive, negative and neutral—transforming in the adjoint representation of SU(2), just like a gauge boson should.

          It’s a wonderful example of how ideas that don’t quite work can still be fruitful. In fact it often feels like Nature is trying to make science easy by obeying not just a single ‘theory of everything’ but a beautifully nested set of better and better approximate theories, starting with ones that use easy math and leading up to more sophisticated ones—sort of like those computer games that have different ‘levels’.

  5. Thomas Larsson says:
    22 September, 2016 at 8:38 pm

    I rarely look at the arxiv these days, but your paper from a couple of weeks ago caught my attention. Probably because I spent most of my career – such as it now was – thinking about the continuum from a dual point of view. If spacetime is a continuum, the points are labelled by real quadruplets, but this labelling is not unique. The numbers are always coordinates relative to some coordinate system, and if you change the coordinate system the numbers change with it. So my take on this was to study the group of permissible coordinate transformations. Exactly what counts as permissible depends on your prejudice, but the biggest possibility is the full group of spacetime diffeomorphisms.

    This point of view is quite fruitful; in particular, it implies all of tensor calculus and differential geometry. Things like tensor densities, exterior and covariant derivatives, etc., all have a natural description in terms of representations of the diffeomorphism group, simply because these concepts make sense; by definition, things that make sense transform as representations, or as morphisms between representations, under the group of coordinate transformations.

    In one dimension we can say more, because the diffeomorphism algebra is also known as the centerless Virasoro algebra. In this case we encounter the standard problems with general-covariant theories – e.g., the absense of local observables – but this defect can be remedied by removing the prefix “centerless”. So my idea was to generalize the Virasoro extension to the diffeomorphism algebra in higher dimension, and in particular to 4D spacetime. I did find (together with a number of mathematicians) the relevant extensions and off-shell representations, but then I failed to make sense of on-shell representations that would be needed to make the connetion to physics.

    Anyway, I recently started my own blog (which I am already neglecting), and wrote up a couple of posts on the subject, starting with this.

    Reply
  6. Struggles with the Continuum (Part 7) | Azimuth says:
    23 September, 2016 at 9:23 pm

    Combining electromagnetism with relativity and quantum mechanics led to QED. Last time we saw the immense struggles with the continuum this caused. But combining gravity with relativity led Einstein to something equally remarkable: general relativity.

    Reply

You can use Markdown or HTML in your comments. You can also use LaTeX, like this: $latex E = m c^2 $. The word 'latex' comes right after the first dollar sign, with a space after it.

This site uses Akismet to reduce spam. Learn how your comment data is processed.