We’ve been looking at how the continuum nature of spacetime poses problems for our favorite theories of physics—problems with infinities. Last time we saw a great example: general relativity predicts the existence of singularities, like black holes and the Big Bang. I explained exactly what these singularities really are. They’re not points or regions of spacetime! They’re more like ways for a particle to ‘fall off the edge of spacetime’. Technically, they are incomplete timelike or null geodesics.
The next step is to ask whether these singularities rob general relativity of its predictive power. The ‘cosmic censorship hypothesis’, proposed by Penrose in 1969, claims they do not.
In this final post I’ll talk about cosmic censorship, and conclude with some big questions… and a place where you can get all these posts in a single file.
Cosmic censorship
To say what we want to rule out, we must first think about what behaviors we consider acceptable. Consider first a black hole formed by the collapse of a star. According to general relativity, matter can fall into this black hole and ‘hit the singularity’ in a finite amount of proper time, but nothing can come out of the singularity.
The time-reversed version of a black hole, called a ‘white hole’, is often considered more disturbing. White holes have never been seen, but they are mathematically valid solutions of Einstein’s equation. In a white hole, matter can come out of the singularity, but nothing can fall in. Naively, this seems to imply that the future is unpredictable given knowledge of the past. Of course, the same logic applied to black holes would say the past is unpredictable given knowledge of the future.
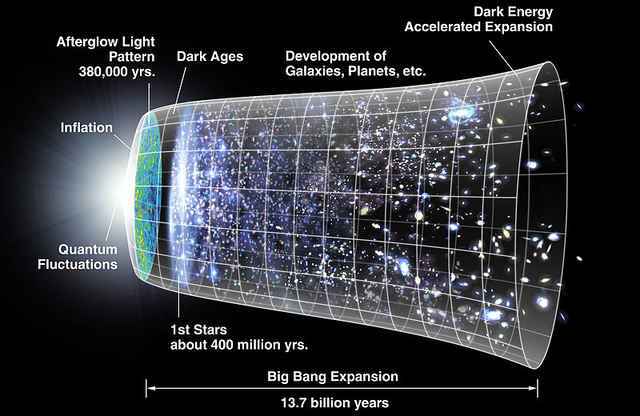
If white holes are disturbing, perhaps the Big Bang should be more so. In the usual solutions of general relativity describing the Big Bang, all matter in the universe comes out of a singularity! More precisely, if one follows any timelike geodesic back into the past, it becomes undefined after a finite amount of proper time. Naively, this may seem a massive violation of predictability: in this scenario, the whole universe ‘sprang out of nothing’ about 14 billion years ago.
However, in all three examples so far—astrophysical black holes, their time-reversed versions and the Big Bang—spacetime is globally hyperbolic. I explained what this means last time. In simple terms, it means we can specify initial data at one moment in time and use the laws of physics to predict the future (and past) throughout all of spacetime. How is this compatible with the naive intuition that a singularity causes a failure of predictability?
For any globally hyperbolic spacetime 
A more challenging example is posed by the Kerr–Newman solution of Einstein’s equation coupled to the vacuum Maxwell equations. When
this solution describes a rotating charged black hole with mass 
this solution gives a spacetime that is not globally hyperbolic: it has closed timelike curves! It also contains a ‘naked singularity’. Roughly speaking, this is a singularity that can be seen by arbitrarily faraway observers in a spacetime whose geometry asymptotically approaches that of Minkowski spacetime. The existence of a naked singularity implies a failure of global hyperbolicity.
The cosmic censorship hypothesis comes in a number of forms. The original version due to Penrose is now called ‘weak cosmic censorship’. It asserts that in a spacetime whose geometry asymptotically approaches that of Minkowski spacetime, gravitational collapse cannot produce a naked singularity.
In 1991, Preskill and Thorne made a bet against Hawking in which they claimed that weak cosmic censorship was false. Hawking conceded this bet in 1997 when a counterexample was found. This features finely-tuned infalling matter poised right on the brink of forming a black hole. It almost creates a region from which light cannot escape—but not quite. Instead, it creates a naked singularity!
Given the delicate nature of this construction, Hawking did not give up. Instead he made a second bet, which says that weak cosmic censorshop holds ‘generically’ — that is, for an open dense set of initial conditions.
In 1999, Christodoulou proved that for spherically symmetric solutions of Einstein’s equation coupled to a massless scalar field, weak cosmic censorship holds generically. While spherical symmetry is a very restrictive assumption, this result is a good example of how, with plenty of work, we can make progress in rigorously settling the questions raised by general relativity.
Indeed, Christodoulou has been a leader in this area. For example, the vacuum Einstein equations have solutions describing gravitational waves, much as the vacuum Maxwell equations have solutions describing electromagnetic waves. However, gravitational waves can actually form black holes when they collide. This raises the question of the stability of Minkowski spacetime. Must sufficiently small perturbations of the Minkowski metric go away in the form of gravitational radiation, or can tiny wrinkles in the fabric of spacetime somehow amplify themselves and cause trouble—perhaps even a singularity? In 1993, together with Klainerman, Christodoulou proved that Minkowski spacetime is indeed stable. Their proof fills a 514-page book.
In 2008, Christodoulou completed an even longer rigorous study of the formation of black holes. This can be seen as a vastly more detailed look at questions which Penrose’s original singularity theorem addressed in a general, preliminary way. Nonetheless, there is much left to be done to understand the behavior of singularities in general relativity.
Conclusions
In this series of posts, we’ve seen that in every major theory of physics, challenging mathematical questions arise from the assumption that spacetime is a continuum. The continuum threatens us with infinities! Do these infinities threaten our ability to extract predictions from these theories—or even our ability to formulate these theories in a precise way?
We can answer these questions, but only with hard work. Is this a sign that we are somehow on the wrong track? Is the continuum as we understand it only an approximation to some deeper model of spacetime? Only time will tell. Nature is providing us with plenty of clues, but it will take patience to read them correctly.
For more
To delve deeper into singularities and cosmic censorship, try this delightful book, which is free online:
• John Earman, Bangs, Crunches, Whimpers and Shrieks: Singularities and Acausalities in Relativistic Spacetimes, Oxford U. Press, Oxford, 1993.
To read this whole series of posts in one place, with lots more references and links, see:
• John Baez, Struggles with the continuum.
• Part 1: introduction; the classical mechanics of gravitating point particles.
• Part 2: the quantum mechanics of point particles.
• Part 3: classical point particles interacting with the electromagnetic field.
• Part 4: quantum electrodynamics.
• Part 5: renormalization in quantum electrodynamics.
• Part 6: summing the power series in quantum electrodynamics.
• Part 7: singularities in general relativity.
• Part 8: cosmic censorship in general relativity; conclusions.
Azimuth 
Very interesting set of posts. Let me mention another twist on the relation between spacetime and continuum, the notion of geometric transition. By replacing the spacetime by a sigma-model whose target is the spacetime and quantizing it, one can sometimes smoothly interpolate between spacetimes of different topology. This goes in the direction of “more continuum” rather than less. For a reference, see for instance Sections 7 and 8 of
https://arxiv.org/abs/hep-th/9702155v1
Yes! By coincidence, I’ve been talking about this with Urs Schreiber over the last few days. You’re alluding to things like ‘flop transitions’ where we have a smoothly varying one-parameter family of conformal field theories, most of which describe strings propagating in Calabi–Yau varieties, but where the Calabi–Yau variety discontinuously ‘flops’ from one topology to another as the parameter crosses a certain value. Here’s one interesting thing: at the value of the parameter where topology changes discontinuously, we get a conformal field theory that does not describe string propagating in a Calabi–Yau variety. Instead, we get a Gepner model, a conformal field theory that is “non-geometric” in that it does not arise as a sigma-model with a manifold as target space.
Among “non-geometric” conformal field theories, some are actually theories where the target space is a noncommutative geometry. Urs pointed out a very nice review article that mentions this idea:
• J. Fröhlich, O. Grandjean and A. Recknagel, Supersymmetric quantum theory, non-commutative geometry, and gravitation, Lecture Notes Les Houches 1995.
For example, they discuss what a noncommutative Kähler manifold should be. But mostly they point to other references:
One reason this is interesting is that it leads to a promising point of contact between string theory and the Barrett–Connes–Lott approach to the Standard Model via noncommutative geometry. I hope Urs will publicly explain this more at some point; it’s a bit technical and I don’t think a blog comment is the right place.
Here is Urs’ post:
• Spectral Standard Model and string compactifications, Physics Forums, 26 September 2016.
Thanks, interesting read. But I have to say that I’m a bit confused about the claims relating the Gepner model to flop transitions. My memories are a bit cloudy, but I thought that the flop transitions, which only involve a collection of cycles shrinking to zero volume, can be seen without leaving the large volume region of the Calabi-Yau. The latter corresponds to the semi-classical regime of the worldsheet theory. On the other hand, the Gepner point is a special point far from the large volume regions, i.e. “very quantum” from the worldsheet point of view, at which the worldsheet theory becomes a rational CFT.
Missing a $latex when introducing the parameter t for the family of Cauchy surfaces: ($t \in \mathbb{R}$) .
Thanks! Fixed.
Your own comment ran into an amusing problem: it’s hard to type
$latex
without having the blog think “hey, what follows should be in latex until I see the next dollar sign!” So when you typed
what we saw on the blog was
So my puzzle is: how do you avoid this problem? How am I typing this:
There should be a latex command that produces a dollar sign; if memory serves. you type, within math mode, a backslash followed by the dollar sign. Lemme see if I get a dollar sign that way (whence the puzzle has a trivial solution, although there may be a more elegant solution).
Test:
.
(Well, that produced a dollar sign that was different from what I was expecting.)
You produced a LaTeX-style dollar sign:
That would certainly suffice for communication purposes! But it looks a bit fancy compared to an ordinary dollar sign:
$
One reason is that WordPress blogs don’t fundamentally use LaTeX: all LaTeX here consists of little gif images, not ordinary text. If you click on your dollar sign, you’ll see it’s really stored here:
https://s0.wp.com/latex.php?latex=%5C%24+&bg=ffffff&fg=333333&s=0
So, suppose one wants to create a dollar sign that looks exactly like this:
$
but with the word ‘latex’ directly after it, like this:
$latex
One needs some other trick.
Sure, sure. Okay, second attempt: use html character code. (Oh, I see a little message just above where I type: “You can use Markdown or HTML in your comments”.)
Okey-dokey, let’s try it. $
So all righty then. $latex And it you want to know how to get that: type $ (let’s see if that works). And if you want to know how I just typed that… we get into a little recursive loop here. :-)
Yes, HTML character codes are the way to go! HTML is more fundamental than LaTeX on WordPress blogs: you can see that by the mayhem that ensues when you try to include the symbols < or > inside a math formula!
And yes, it’s amusingly difficult to talk about an HTML character code on a WordPress blog, because to do so you need to use the HTML character code for at least one character in the HTML character code. We’re practically skating on the brink of Gödel’s incompleteness theorem here.
So I’m not a physics guy and find it difficult to make it past the math and names of anyone other than Einstein and Hawking in this post, but I like to think, andsince you linked the big bang to a white hole, this got me thinking. Maybe the big bang is the only white hole? Particles have been, and are still pouring out of it (which makes me comfortable in my mind to comprehend how quantum physics works). If that’s the case, would this make black holes one way where where particles fall back, or equalize, to whatever null space they came from? Our universe, and continuum, is just the result of the in-between?
Up till now, I’ve been gathering our understanding of physics is that: only the continuum exists, and something plucked its strings as a big bang. The reverberations manifest to us as particles. This is what I gathered after first hearing about string theory and its incarnations. I like the poetic nature of this theory because it describes our universe as a song with harmonies.
Still for some reason, I’ve never been comfortable with the continuum. I want it to be more tangible. You could explain it to me as the force between any two particles at any distance and I would accept that, because really I believe only the null exists. I just cannot take in faith that some invisible fabric of the universe just exists to make our maths work. I cannot comprehend any other way I could explain what holds the universe together, and why light only goes one speed. Why is there only one continuum? For me, a continuum only exists because of the existence of at least two particles and their interactions in null space. That makes it tangible for me.
If you had two universes that only comprised of two particles each, and the respective universes’ particles could not interact with each other, if the universes passed by each other at 25 miles an hour relative to each other in null space, then wouldn’t their individual light particles then be travelling at the speed of light plus 25 miles a hour relative to each other, a speed limit illegal to break in physics? I return to this elementary level of the theory of relativity everytime I try to wrap my head around a continuum and that it just doesn’t sit right with me.
You could argue however, if null space is the only thing that exists, then by just adding one particle to it you have created a continuum and eliminated null space, because anything beyond that particle, out to infinity, will happen in relation to it, thereby beholden to that speed of light constant. By adding that one particle, you just created an anchor for the continuum.
Jacob S. wrote:
People have definitely considered this idea. It’s pretty interesting.
When one is an amateur in a subject, it’s fun to try to come up with new ideas. In a subject like general relativity, it’s easy to come up with new ideas that most physicists will consider complete nonsense. It’s hard to come up with ideas that they’ll take seriously—and almost all ideas like that will have already been studied. So, you should feel glad that you’ve come up with one of those.
In my first attempt to publish a math paper, back when I was in high school, I showed that if you take two very large numbers, the probability that they’re relatively prime is 6/π2. I thought that was really cool. I submitted this paper to the American Mathematical Monthly, a journal for college students and college math teachers. I got a short rejection notice saying this had been proved a long long time ago. It hurt but it was an educational experience. Later I learned to be happy when some discovery of mine was already known—as long as it had first been discovered by someone good.
Now, luckily, we have blogs and other places where people can ask about things. But it can still be painful. For example, on MathOverflow I see someone got slapped down for even asking what was the probability that two large numbers is relatively prime. But at least people carefully answered the question before ‘closing’ it for being ‘too localized’. A wiser approach would have been for this questioner to humbly go to Math Stackexchange before trying MathOverflow. I’m reminded of this quote from Hua Loo-Keng’s Introduction to Number Theory:
But anyway, I’m not trying to hassle you or make you feel bad, I’m just digressing. Number theory is a particularly tough game to start playing.
Back to white holes! The usual Big Bang cosmology is different than a white hole because it’s isotropic (no matter which direction you look, things look the same, at least on large enough scales) and homogeneous (every region looks just like every other, at least on large enough scales). A white hole has a specific location, whereas the Big Bang happened everywhere at once.
However, if all the galaxies we see were shooting out of a really really huge white hole, they would look almost isotropic and homogeneous as long as we didn’t look to far. (It’s a lot like how the Earth seems flat if you don’t look too far.) We’d see an expanding universe, rather similar to the Big Bang cosmology.
One problem with this idea is that there’s nothing it explains better than the usual Big Bang cosmology. There are probably also ways in which it’s worse, which I could try to explain if required. I don’t know if anyone has investigated this in detail. However, in their rather nice article on white holes, Wikipedia writes:
Here’s the paper:
• A. Retter and S. Heller, The revival of white holes as Small Bangs, New Astronomy 17 (2011), 73–75.
So I’d start here, and in the references, if I wanted to think more about white hole cosmologies.
I don’t at all believe white holes are a promising alternative to the Big Bang, because I see no problem that they solve better than the Big Bang. I am, however interested in white holes for completely different reasons, mainly just for fun. If you’re curious about those reasons, here are some things to read:
• John Baez, Black hole plus white hole equals wormhole, 15 September 2015. (The commments by Phil Gibbs lead to a very interesting discussion.)
• John Baez, Black hole versus white hole, 21 September 2016. (This will make more sense if you first read my previous post Understanding black holes).
Jacob S. wrote:
My problem here is that I don’t know what ‘null space’ is supposed to mean. It’s not a thing in general relativity, or in any other theory I know.
It is the absence of any particles or energy or time, including the fabric of space, basically zero, if not well beyond zero: null. I think of it like an empty computer file ready to add data. Until that happens all values are null. Until our universe existed, it didn’t exist. It was null.
In this null space, when you add one to zero you must balance it with a negative one. That in between is the universe. This is just a thing I like to play around with. It’s not quite as much a hypothesis for physics than it is a modus for me to approach physics ideas on a more philosophical level, since I’m not that great at math, well certainly not as good as physicists. The hypothesis comes in that everything was once null, and something caused it to have value, but if you add everything together it still equals zero and camels itself out.
I first toyed with this I first heard about string theory. If particles are metaphorically strings vibrating at different frequencies to produce their properties and how they react with other particles, then they must be vibrating back and forth across a zero value. When combined with all particles this is the ‘song’ of the universe. If you were to silence that vibration we would be back to zero. Nothing would exist.
I still struggle with this because it means something has to vibrate. That would mean the universe is only a continuum, and what we see from it are properties produced from that fabric vibrating. If you silenced all the vibrations it equals zero. But zero is still a value, and null is no value. If you silence the universe and return to it zero, does that also return it to null?
What makes up this fabric of space-time then to even have a zero value and dictate all our physical laws? There must be a null space that the fabric exists within and some means that generated our space to anchor that fabric into space.
That question will be the death of me, especially since I don’t have the right type of mind to do the math and figure it out, or make it halfway through a paper written by someone who can.
Okay, so “null space” is your own personal idea. It resembles the concept of the “vacuum”, which has been studied intensively in quantum field theory and general relativity. You can start learning about it here:
• Vacuum state, Wikipedia.
Thank you.
John wrote:
Interestingly, this is most likely not true for AdS see e.g.
• Resonant dynamics and the instability of anti-de Sitter spacetime, Resonant dynamics and the instability of anti-de Sitter spacetim.
I am not sure what this means, if anything, for AdS/CFT …
That’s very interesting! Since I’m not fond of the AdS/CFT craze I would be happy to see anti-deSitter spacetime unstable.
However, the article only claims to show instability of anti-deSitter spacetime together with a massless scalar field. The famous work of Christodoulou and Klainerman only showed stability of Minkowski spacetime as a solution of Einstein’s equations, not Einstein’s equations coupled to a massless scalar field. So, we don’t have a perfect comparison between the two cases.
I looked at the paper, and there’s another point of dissimilarity. This paper only addresses 5-dimensional anti-deSitter spacetime, while Christodoulou and Klainerman only studied 4-dimensional Minkowski spacetime. The authors of this paper say they’ll tackle other dimensions later.
The first paragraph is interesting:
When you look at the reference, you’ll see that they’re again talking about Einstein’s equation coupled to a massless scalar field. However, they’re doing numerical simulations in 4d, not 5d.
Btw there is a youtube video with Piotr talking about all this http://www.youtube.com/watch?v=l5JVE9UsCGU
The instability of AdS has gotten a few minutes of fame, receiving an article in Quanta magazine. It looks like a decent write-up, except for a part that confuses the geometry of AdS spacetime with ordinary special relativity. The main technical paper they point to is arXiv:1812.04268.
On the one hand, these various instability results seem natural, in a fashion. If you want thermalization to happen in the boundary field theory, then you want black-hole formation to happen in the bulk gravitational theory. But on the other hand, the radical difference in stability properties makes me question just how much AdS quantum gravity can tell us about quantum gravity in our universe. The line all along was, “You can put whatever local physics you want into an AdS box!” Yet the very property of AdS that makes it a good background for quantum gravity — it’s a convenient box to put gravity in — means that the answer to questions like, “If I do this in my lab, will a black hole happen?” might be different. To me, this calls into question the idea that well-defined measurements are the same in AdS and in dS or Minkowski, which in turn leads me to speculate that the meaning of the verb “to quantize” cannot be the same.
But that’s freewheeling chatter on my part; mostly I’m just here to leave a couple links in case anybody is curious.
Does anyone else sometimes think that “singularity” is a complete misnomer when, in fact, there are apparently so many of them? I realize that the concept of ‘singularity’ is mostly a mathematical and physical one, but the linguistic problem with the much-repeated use of the term ‘singularity’ is that it implies uniqueness — i.e. that there is only one of them. I can see the appropriateness of calling the Big Bang a singularity, but to call every Black hole a ‘singularity’ is much more problematic.
Still, my opinion is that even the Big Bang itself is hardly a singular event — even if technically a ‘singularity’, because I embrace the Turok-Steinhardt model of an ekpyrotic universe, based on my own mentation, studies, and quasi-religious beliefs. Black holes, on the other hand, or even cosmic strings for that matter, are clearly not singular in any sense of the word, even if there is no ekpyrotic (cyclic) aspect to the Multiverse/Universe.
If you look up “singular” in any dictionary, it will give meanings like “extraordinary, remarkable” or “unusual, strange, odd” along with (and usually before) the meaning “unique”. The ordinary English usage has long included things that are merely strange or exceptional within some particular context, rather than being literally unique.
This claim seems hard to understand in the context of a universe containing two spatially separated black holes. Am I missing something?
Yes. I see why what I said is confusing. I’m talking about slicing spacetime into Cauchy surfaces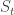
, which are spacelike hypersurfaces such that every timelike or lightlike curve crosses each surface 
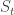in exactly one point.
We have to be rather careful to find these surfaces in spacetime with one or more black holes in it. In particular, as
increases, we have to push the surface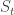 
‘forward in time’, but we have to do it slower and slower inside any black hole, so that the surface never actually hits a singularity.
Thus, “the singularity is in the future of all these surfaces”. Or, if you have more than one black hole, “the singularities are in the future of all these surfaces”.
To achieve this, the parameter
can’t be anything like the ‘proper time’ ticked out by a freely falling particle. The trajectory of a freely falling particle that ‘hits the singularity’ will become undefined in a finite amount of proper time. But the surfaces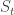 
need to be well-defined Cauchy surfaces for arbitrarily large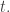 
Have you considered making a book with some of the series of posts of this blog, such as this one, the “Mathematiccs of the Environment”, and others?
Perhaps just the material posted here or with some addenda. Terence Tao has done it with some of the entries of his blog (and sure there are many other cases), and in my humble opinion there are material here of considerable interest for people with different backgrounds.
Thank you for writing this paper! I re-posted the link to it here
http://fqxi.org/community/forum/topic/2685
Thanks!
Well, quantum field theory threatens us with singularities (particles). It seems like a common feature of everyday physics. It is exotic physics, like string theory, that removes some or, hopefully, all.
I don’t know what you have in mind by saying that particles in quantum field theory are “singularities”.
A wonderful series of posts on the continuum and the problems it generates in physics. Problems that should not exist. Problems of our own making. I believe “space-time” is not fundamental, but an emergent property of something deeper and simpler!
Go for it! I spent 10 years trying to find that deeper and simpler thing, and I came up with spin foam models. I quit when I realized it would take a lot more work to see if they successfully deal with problems in physics.
Yes. If you pick a mathematical object to model reality (and very often the object is a derivative or partial derivative) then you implicitly assume all the baggage that comes with the object. In this case that space is a continuum. Then if it’s not you pay the price. Infinities everywhere. And infinities of your own making! (For example: renormalization of QED.)
The problems I’m describing are mathematical: they exist in the math whether or not that math accurately models reality. So while you say
in fact even if spacetime is a continuum we pay the price of having to work with this.
Did you read these parts?
• Part 4: quantum electrodynamics.
• Part 5: renormalization in quantum electrodynamics.
One that’s clear by now is that renormalization is a real physical phenomenon, regardless of whether spacetime is ultimately a continuum or not. It arises because each particle is surrounded by a cloud of virtual particles, so that its observed properties change as one penetrates deeper into that cloud. This is observed experimentally. The problem with the continuum is simply that in some cases this effect would go on forever.
Good point about QED renormalization being more complex than just a continuum problem.. but yet I wonder.. if we had a totally different formalism from the outset would it still exist?
When you smack electrons against each other harder, they act like their charge is bigger. I don’t believe that will go away with a different formalism. Renormalization relates their charge at high momenta to their charge at low momenta. It does so very accurately. I don’t think we want that to go away.
When we extrapolate this to arbitrarily high momenta, things go crazy. I think we do want that to go away: that’s an artifact of assuming spacetime can be arbitrarily subdivided. (In relativistic quantum physics, particles are waves and their momentum is inversely proportional to their wavelength.)
All decent physicists know this; getting a workable theory with spacetime not a continuum is the hard part. A bunch of very smart people have worked on that for many years, and so have I. As you can probably tell, it irks me when people say “Hey! Why don’t you just stop assuming spacetime is a continuum?”—as if we’re obstinately refusing to consider an easy solution to our problems. I’m not accusing you of doing that, but lots of people do that.