Combining electromagnetism with relativity and quantum mechanics led to QED. Last time we saw the immense struggles with the continuum this caused. But combining gravity with relativity led Einstein to something equally remarkable: general relativity.
In general relativity, infinities coming from the continuum nature of spacetime are deeply connected to its most dramatic successful predictions: black holes and the Big Bang. In this theory, the density of the Universe approaches infinity as we go back in time toward the Big Bang, and the density of a star approaches infinity as it collapses to form a black hole. Thus we might say that instead of struggling against infinities, general relativity accepts them and has learned to live with them.
General relativity does not take quantum mechanics into account, so the story is not yet over. Many physicists hope that quantum gravity will eventually save physics from its struggles with the continuum! Since quantum gravity far from being understood, this remains just a hope. This hope has motivated a profusion of new ideas on spacetime: too many to survey here. Instead, I’ll focus on the humbler issue of how singularities arise in general relativity—and why they might not rob this theory of its predictive power.
General relativity says that spacetime is a 4-dimensional Lorentzian manifold. Thus, it can be covered by patches equipped with coordinates, so that in each patch we can describe points by lists of four numbers. Any curve going through a point then has a tangent vector
whose components are
Furthermore, given two tangent vectors
at the same point we can take their inner product
where as usual we sum over repeated indices, and is a
matrix called the metric, depending smoothly on the point. We require that at any point we can find some coordinate system where this matrix takes the usual Minkowski form:
However, as soon as we move away from our chosen point, the form of the matrix in these particular coordinates may change.
General relativity says how the metric is affected by matter. It does this in a single equation, Einstein’s equation, which relates the ‘curvature’ of the metric at any point to the flow of energy-momentum through that point. To define the curvature, we need some differential geometry. Indeed, Einstein had to learn this subject from his mathematician friend Marcel Grossman in order to write down his equation. Here I will take some shortcuts and try to explain Einstein’s equation with a bare minimum of differential geometry. For how this approach connects to the full story, and a list of resources for further study of general relativity, see:
• John Baez and Emory Bunn, The meaning of Einstein’s equation.
Consider a small round ball of test particles that are initially all at rest relative to each other. This requires a bit of explanation. First, because spacetime is curved, it only looks like Minkowski spacetime—the world of special relativity—in the limit of very small regions. The usual concepts of ’round’ and ‘at rest relative to each other’ only make sense in this limit. Thus, all our forthcoming statements are precise only in this limit, which of course relies on the fact that spacetime is a continuum.
Second, a test particle is a classical point particle with so little mass that while it is affected by gravity, its effects on the geometry of spacetime are negligible. We assume our test particles are affected only by gravity, no other forces. In general relativity this means that they move along timelike geodesics. Roughly speaking, these are paths that go slower than light and bend as little as possible. We can make this precise without much work.
For a path in space to be a geodesic means that if we slightly vary any small portion of it, it can only become longer. However, a path in spacetime traced out by particle moving slower than light must be ‘timelike’, meaning that its tangent vector
satisfies
We define the proper time along such a path from
to
to be
This is the time ticked out by a clock moving along that path. A timelike path is a geodesic if the proper time can only decrease when we slightly vary any small portion of it. Particle physicists prefer the opposite sign convention for the metric, and then we do not need the minus sign under the square root. But the fact remains the same: timelike geodesics locally maximize the proper time.
Actual particles are not test particles! First, the concept of test particle does not take quantum theory into account. Second, all known particles are affected by forces other than gravity. Third, any actual particle affects the geometry of the spacetime it inhabits. Test particles are just a mathematical trick for studying the geometry of spacetime. Still, a sufficiently light particle that is affected very little by forces other than gravity can be approximated by a test particle. For example, an artificial satellite moving through the Solar System behaves like a test particle if we ignore the solar wind, the radiation pressure of the Sun, and so on.
If we start with a small round ball consisting of many test particles that are initially all at rest relative to each other, to first order in time it will not change shape or size. However, to second order in time it can expand or shrink, due to the curvature of spacetime. It may also be stretched or squashed, becoming an ellipsoid. This should not be too surprising, because any linear transformation applied to a ball gives an ellipsoid.
Let be the volume of the ball after a time
has elapsed, where time is measured by a clock attached to the particle at the center of the ball. Then in units where
Einstein’s equation says:
These flows here are measured at the center of the ball at time zero, and the coordinates used here take advantage of the fact that to first order, at any one point, spacetime looks like Minkowski spacetime.
The flows in Einstein’s equation are the diagonal components of a matrix
called the ‘stress-energy tensor’. The components
of this matrix say how much momentum in the
direction is flowing in the
direction through a given point of spacetime. Here
and
range from
to
corresponding to the
and
coordinates.
For example, is the flow of
-momentum in the
-direction. This is just the energy density, usually denoted
The flow of
-momentum in the
-direction is the pressure in the
direction, denoted
and similarly for
and
You may be more familiar with direction-independent pressures, but it is easy to manufacture a situation where the pressure depends on the direction: just squeeze a book between your hands!
Thus, Einstein’s equation says
It follows that positive energy density and positive pressure both curve spacetime in a way that makes a freely falling ball of point particles tend to shrink. Since and we are working in units where
ordinary mass density counts as a form of energy density. Thus a massive object will make a swarm of freely falling particles at rest around it start to shrink. In short, gravity attracts.
Already from this, gravity seems dangerously inclined to create singularities. Suppose that instead of test particles we start with a stationary cloud of ‘dust’: a fluid of particles having nonzero energy density but no pressure, moving under the influence of gravity alone. The dust particles will still follow geodesics, but they will affect the geometry of spacetime. Their energy density will make the ball start to shrink. As it does, the energy density will increase, so the ball will tend to shrink ever faster, approaching infinite density in a finite amount of time. This in turn makes the curvature of spacetime become infinite in a finite amount of time. The result is a ‘singularity’.
In reality, matter is affected by forces other than gravity. Repulsive forces may prevent gravitational collapse. However, this repulsion creates pressure, and Einstein’s equation says that pressure also creates gravitational attraction! In some circumstances this can overwhelm whatever repulsive forces are present. Then the matter collapses, leading to a singularity—at least according to general relativity.
When a star more than 8 times the mass of our Sun runs out of fuel, its core suddenly collapses. The surface is thrown off explosively in an event called a supernova. Most of the energy—the equivalent of thousands of Earth masses—is released in a ten-second burst of neutrinos, formed as a byproduct when protons and electrons combine to form neutrons. If the star’s mass is below 20 times that of our the Sun, its core crushes down to a large ball of neutrons with a crust of iron and other elements: a neutron star.
However, this ball is unstable if its mass exceeds the Tolman–Oppenheimer–Volkoff limit, somewhere between 1.5 and 3 times that of our Sun. Above this limit, gravity overwhelms the repulsive forces that hold up the neutron star. And indeed, no neutron stars heavier than 3 solar masses have been observed. Thus, for very heavy stars, the endpoint of collapse is not a neutron star, but something else: a black hole, an object that bends spacetime so much even light cannot escape.
If general relativity is correct, a black hole contains a singularity. Many physicists expect that general relativity breaks down inside a black hole, perhaps because of quantum effects that become important at strong gravitational fields. The singularity is considered a strong hint that this breakdown occurs. If so, the singularity may be a purely theoretical entity, not a real-world phenomenon. Nonetheless, everything we have observed about black holes matches what general relativity predicts. Thus, unlike all the other theories we have discussed, general relativity predicts infinities that are connected to striking phenomena that are actually observed.
The Tolman–Oppenheimer–Volkoff limit is not precisely known, because it depends on properties of nuclear matter that are not well understood. However, there are theorems that say singularities must occur in general relativity under certain conditions.
One of the first was proved by Raychauduri and Komar in the mid-1950’s. It applies only to ‘dust’, and indeed it is a precise version of our verbal argument above. It introduced the Raychauduri’s equation, which is the geometrical way of thinking about spacetime curvature as affecting the motion of a small ball of test particles. It shows that under suitable conditions, the energy density must approach infinity in a finite amount of time along the path traced out out by a dust particle.
The first required condition is that the flow of dust be initally converging, not expanding. The second condition, not mentioned in our verbal argument, is that the dust be ‘irrotational’, not swirling around. The third condition is that the dust particles be affected only by gravity, so that they move along geodesics. Due to the last two conditions, the Raychauduri–Komar theorem does not apply to collapsing stars.
The more modern singularity theorems eliminate these conditions. But they do so at a price: they require a more subtle concept of singularity! There are various possible ways to define this concept. They’re all a bit tricky, because a singularity is not a point or region in spacetime.
For our present purposes, we can define a singularity to be an ‘incomplete timelike or null geodesic’. As already explained, a timelike geodesic is the kind of path traced out by a test particle moving slower than light. Similarly, a null geodesic is the kind of path traced out by a test particle moving at the speed of light. We say a geodesic is ‘incomplete’ if it ceases to be well-defined after a finite amount of time. For example, general relativity says a test particle falling into a black hole follows an incomplete geodesic. In a rough-and-ready way, people say the particle ‘hits the singularity’. But the singularity is not a place in spacetime. What we really mean is that the particle’s path becomes undefined after a finite amount of time.
We need to be a bit careful about what we mean by ‘time’ here. For test particles moving slower than light this is easy, since we can parametrize a timelike geodesic by proper time. However, the tangent vector of a null geodesic has
so a particle moving along a null geodesic does not experience any passage of proper time. Still, any geodesic, even a null one, has a family of preferred parametrizations. These differ only by changes of variable like this:
By ‘time’ we really mean the variable
in any of these preferred parametrizations. Thus, if our spacetime is some Lorentzian manifold
we say a geodesic
is incomplete if, parametrized in one of these preferred ways, it cannot be extended to a strictly longer interval.
The first modern singularity theorem was proved by Penrose in 1965. It says that if space is infinite in extent, and light becomes trapped inside some bounded region, and no exotic matter is present to save the day, either a singularity or something even more bizarre must occur. This theorem applies to collapsing stars. When a star of sufficient mass collapses, general relativity says that its gravity becomes so strong that light becomes trapped inside some bounded region. We can then use Penrose’s theorem to analyze the possibilities.
Shortly thereafter Hawking proved a second singularity theorem, which applies to the Big Bang. It says that if space is finite in extent, and no exotic matter is present, generically either a singularity or something even more bizarre must occur. The singularity here could be either a Big Bang in the past, a Big Crunch in the future, both—or possibly something else. Hawking also proved a version of his theorem that applies to certain Lorentzian manifolds where space is infinite in extent, as seems to be the case in our Universe. This version requires extra conditions.
There are some undefined phrases in this summary of the Penrose–Hawking singularity theorems, most notably these:
• ‘exotic matter’
• ‘something even more bizarre’.
So, let me say a bit about each.
These singularity theorems precisely specify what is meant by ‘exotic matter’. All known forms of matter obey the ‘dominant energy condition’, which says that
at all points and in all locally Minkowskian coordinates. Exotic matter is anything that violates this condition.
The Penrose–Hawking singularity theorems also say what counts as ‘something even more bizarre’. An example would be a closed timelike curve. A particle following such a path would move slower than light yet eventually reach the same point where it started—and not just the same point in space, but the same point in spacetime! If you could do this, perhaps you could wait, see if it would rain tomorrow, and then go back and decide whether to buy an umbrella today. There are certainly solutions of Einstein’s equation with closed timelike curves. The first interesting one was found by Einstein’s friend Gödel in 1949, as part of an attempt to probe the nature of time. However, closed timelike curves are generally considered less plausible than singularities.
In the Penrose–Hawking singularity theorems, ‘something even more bizarre’ means that spacetime is not ‘globally hyperbolic’. To understand this, we need to think about when we can predict the future or past given initial data. When studying field equations like Maxwell’s theory of electromagnetism or Einstein’s theory of gravity, physicists like to specify initial data on space at a given moment of time. However, in general relativity there is considerable freedom in how we choose a slice of spacetime and call it ‘space’. What should we require? For starters, we want a 3-dimensional submanifold of spacetime that is ‘spacelike’: every vector
tangent to
should have
However, we also want any timelike or null curve to hit
exactly once. A spacelike surface with this property is called a Cauchy surface, and a Lorentzian manifold containing a Cauchy surface is said to be globally hyperbolic. There are many theorems justifying the importance of this concept. Globally hyperbolicity excludes closed timelike curves, but also other bizarre behavior.
By now the original singularity theorems have been greatly generalized and clarified. Hawking and Penrose gave a unified treatment of both theorems in 1970. The 1973 textbook by Hawking and Ellis gives a systematic introduction to this subject. Hawking gave an elegant informal overview of the key ideas in 1994, and a paper by Garfinkle and Senovilla reviews the subject and its history up to 2015.
If we accept that general relativity really predicts the existence of singularities in physically realistic situations, the next step is to ask whether they rob general relativity of its predictive power. I’ll talk about that next time!
• Part 1: introduction; the classical mechanics of gravitating point particles.
• Part 2: the quantum mechanics of point particles.
• Part 3: classical point particles interacting with the electromagnetic field.
• Part 4: quantum electrodynamics.
• Part 5: renormalization in quantum electrodynamics.
• Part 6: summing the power series in quantum electrodynamics.
• Part 7: singularities in general relativity.
• Part 8: cosmic censorship in general relativity; conclusions.


I’ve been figuratively holding my breath since I started reading this series. Feels like reading some high quality sci-fi. Thank you!
Sure, you’re welcome! Science is usually more amazing than science fiction, because nature is inexhaustibly strange—yet perfectly logical, in retrospect.
I always look forward to your series posts. Also, the ‘Last time’ link is broken again!
Thanks again! I changed the schedule for these posts to be published when I decided to blog about my use of Twitter. That broke all these links, since the links include the date of publication.
There’s just one more post coming up! Let’s see if I can fix any links ahead of time.
You said a few times “if no exotic matter is present.” Is dark matter exotic for these purposes?
No. I defined exotic matter:
If you look at my formulation of Einstein’s equation you’ll see this is matter that creates a repulsive gravitational field. Dark matter needs to create an attractive gravitational field or it wouldn’t do what we need it to: help form galaxies and make them spin as fast as observed.
This condition
when it holds at every point in every coordinate system, is called the strong energy condition. Using Einstein’s equations it’s equivalent to saying
for every timelike vector field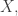 where
where  is the Ricci tensor. There’s no reason to think it’s violated by dark matter, but it is violated by ‘dark energy’, which does create a repulsive gravitational field. ‘Dark energy’, also known as a ‘positive cosmological constant’, amounts to having a constant small positive energy density
is the Ricci tensor. There’s no reason to think it’s violated by dark matter, but it is violated by ‘dark energy’, which does create a repulsive gravitational field. ‘Dark energy’, also known as a ‘positive cosmological constant’, amounts to having a constant small positive energy density 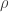 throughout space, and an equal but opposite pressure in every direction, making
throughout space, and an equal but opposite pressure in every direction, making
The repulsive gravitational field of dark energy is making the universe expand faster and faster!
However, there are other, better singularity theorems that involve energy conditions like the dominant energy condition, which are not violated by dark energy.
So, these days dark energy is generally not considered ‘exotic matter’, despite what I seem to suggest in this article, and despite the fact that dark energy is ‘exotic’ in the nontechnical sense of being weird.
Doesn’t the Casimir effect (with an appropriate geometry of the conducting surfaces) exhibit a violation of the strong energy condition (and even the Null energy condition)? Do you have in mind an averaged version of the strong energy condition?
Yes, I think the Casimir effect violates the strong energy condition: the vacuum between two conductive plates parallel to the plane has
plane has
so
As you probably know better than me, people have investigated quite a number of energy conditions and tried to determine what good behaviors general relativity has when they hold and what bad behaviors it can have when they fail. I’m no expert on this, so anyone interested should probably start here:
• Erik Curiel, A primer on energy conditions.
We’ve been looking at how the continuum nature of spacetime poses problems for our favorite theories of physics—problems with infinities. Last time we saw a great example: general relativity predicts the existence of singularities, like black holes and the Big Bang. I explained exactly what these singularities really are. They’re not points or regions of spacetime! They’re more like ways for a particle to ‘fall off the edge of spacetime’. Technically, they are incomplete timelike or null geodesics.
The next step is to ask whether these singularities rob general relativity of its predictive power. The ‘cosmic censorship hypothesis’, proposed by Penrose in 1969, claims they do not.