I can’t help thinking about geometric quantization. I feel it holds some lessons about the relation between classical and quantum mechanics that we haven’t fully absorbed yet. I want to play my cards fairly close to my chest, because there are some interesting ideas I haven’t fully explored yet… but still, there are also plenty of ‘well-known’ clues that I can afford to explain.
The first one is this. As beginners, we start by thinking of geometric quantization as a procedure for taking a symplectic manifold and constructing a Hilbert space: that is, taking a space of classical states and contructing the corresponding space of quantum states. We soon learn that this procedure requires additional data as its input: a symplectic manifold is not enough. We learn that it works much better to start with a Kähler manifold equipped with a holomorphic hermitian line bundle with a connection whose curvature is the imaginary part of the Kähler structure. Then the space of holomorphic sections of that line bundle gives the Hilbert space we seek.
That’s quite a mouthful—but it makes for such a nice story that I’d love to write a bunch of blog articles explaining it with lots of examples. Unfortunately I don’t have time, so try these:
• Matthias Blau, Symplectic geometry and geometric quantization.
• A. Echeverria-Enriquez, M.C. Munoz-Lecanda, N. Roman-Roy, C. Victoria-Monge, Mathematical foundations of geometric quantization.
But there’s a flip side to this story which indicates that something big and mysterious is going on. Geometric quantization is not just a procedure for converting a space of classical states into a space of quantum states. It also reveals that a space of quantum states can be seen as a space of classical states!
To reach this realization, we must admit that quantum states are not really vectors in a Hilbert space 
So a space of quantum states is an example of a space of classical states—equipped with precisely all the complicated extra structure that lets us geometrically quantize it!
At this point, if you don’t already know the answer, you should be asking: and what do we get when we geometrically quantize it?
The answer is exciting only in that it’s surprisingly dull: when we geometrically quantize 
You may have heard of ‘second quantization’, where we take a quantum system, treat it as classical, and quantize it again. In the usual story of second quantization, the new quantum system we get is more complicated than the original one… and we can repeat this procedure again and again, and keep getting more interesting things:
• John Baez, Nth quantization.
The story I’m telling now is different. I’m saying that when we take a quantum system with Hilbert space 
The two stories are not in contradiction, because they rely on two different notions of what it means to ‘think of a quantum system as classical’. In today’s story that means getting a symplectic manifold 
I should explain the relation of these two stories, but that would be a big digression from today’s intended blog article: indeed I’m already regretting having drifted off course. I only brought up this other story to heighten the mystery I’m talking about now: namely, that when we geometrically quantize the space
The math is not mysterious here; it’s the physical meaning of the math that’s mysterious. The math seems to be telling us that contrary to what they say in school, quantum systems are special classical systems, with the special property that when you quantize them nothing new happens!
This idea is not mine; it goes back at least to Kibble, the guy who with Higgs invented the method whereby the Higgs boson does its work:
• Tom W. B. Kibble, Geometrization of quantum mechanics, Comm. Math. Phys. 65 (1979), 189–201.
This led to a slow, quiet line of research that continues to this day. I find this particular paper especially clear and helpful:
• Abhay Ashtekar, Troy A. Schilling, Geometrical formulation of quantum mechanics, in On Einstein’s Path, Springer, Berlin, 1999, pp. 23–65.
so if you’re wondering what the hell I’m talking about, this is probably the best place to start. To whet your appetite, here’s the abstract:
Abstract. States of a quantum mechanical system are represented by rays in a complex Hilbert space. The space of rays has, naturally, the structure of a Kähler manifold. This leads to a geometrical formulation of the postulates of quantum mechanics which, although equivalent to the standard algebraic formulation, has a very different appearance. In particular, states are now represented by points of a symplectic manifold (which happens to have, in addition, a compatible Riemannian metric), observables are represented by certain real-valued functions on this space and the Schrödinger evolution is captured by the symplectic flow generated by a Hamiltonian function. There is thus a remarkable similarity with the standard symplectic formulation of classical mechanics. Features—such as uncertainties and state vector reductions—which are specific to quantum mechanics can also be formulated geometrically but now refer to the Riemannian metric—a structure which is absent in classical mechanics. The geometrical formulation sheds considerable light on a number of issues such as the second quantization procedure, the role of coherent states in semi-classical considerations and the WKB approximation. More importantly, it suggests generalizations of quantum mechanics. The simplest among these are equivalent to the dynamical generalizations that have appeared in the literature. The geometrical reformulation provides a unified framework to discuss these and to correct a misconception. Finally, it also suggests directions in which more radical generalizations may be found.
Personally I’m not interested in the generalizations of quantum mechanics: I’m more interested in what this circle of ideas means for quantum mechanics.
One rather cynical thought is this: when we start our studies with geometric quantization, we naively hope to extract a space of quantum states from a space of classical states, e.g. a symplectic manifold. But we then discover that to do this in a systematic way, we need to equip our symplectic manifold with lots of bells and whistles. Should it really be a surprise that when we’re done, the bells and whistles we need are exactly what a space of quantum states has?
I think this indeed dissolves some of the mystery. It’s a bit like the parable of ‘stone soup’: you can make a tasty soup out of just a stone… if you season it with some vegetables, some herbs, some salt and such.
However, perhaps because by nature I’m an optimist, I also think there are interesting things to be learned from the tight relation between quantum and classical mechanics that appears in geometric quantization. And I hope to talk more about those in future articles.
• Part 1: the mystery of geometric quantization: how a quantum state space is a special sort of classical state space.
• Part 2: the structures besides a mere symplectic manifold that are used in geometric quantization.
• Part 3: geometric quantization as a functor with a right adjoint, ‘projectivization’, making quantum state spaces into a reflective subcategory of classical ones.
• Part 4: making geometric quantization into a monoidal functor.
• Part 5: the simplest example of geometric quantization: the spin-1/2 particle.
• Part 6: quantizing the spin-3/2 particle using the twisted cubic; coherent states via the adjunction between quantization and projectivization.
• Part 7: the Veronese embedding as a method of ‘cloning’ a classical system, and taking the symmetric tensor powers of a Hilbert space as the corresponding method of cloning a quantum system.
• Part 8: cloning a system as changing the value of Planck’s constant.
Azimuth 
Hi John,
What bothers me about geometric quantization is that it gives you quantum states nicely (besides “holomorphic sections of a line bundle”, there’s also “index of the Dirac operator for a chosen Spin-c structure”) but not operators on them.
For an alternate take on quantization that starts with operators, but only works for special phase spaces, for any Lie algebra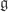
take as your classical Poisson manifold 
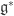, the dual of the Lie algebra. The Poisson bracket on linear functions on this space is just the Lie bracket, and you extend to all functions by insisting on the Leibniz rule.
Quantization of this is given by the universal enveloping algebra
, which gives you abstractly operators, your problem is to find the possible state spaces (the representations of the Lie algebra).
To construct irreducible state spaces, you look at orbits of the Lie group action on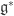
. On these manifolds the Poisson bracket gives a symplectic structure and you can try and do geometric quantiation to get the representations (this is the “Orbit method” of representation theory).
Hi! It looks like the first time you’ve commented here!
I wouldn’t go that far.
Geometric quantization of Kähler manifolds equipped with all the extra data I mentioned is functorial, so ‘classical symmetries’ (holomorphic isometries of these manifolds equipped with lifts to their holomorphic hermitian line bundles) give ‘quantum symmetries’ (unitary operators on their Hilbert spaces), so ‘infinitesimal classical symmetries’ give ‘infinitesimal quantum symmetries’ (self-adjoint operators). This is a way to get operators.
Admittedly, this procedure for getting operators rather limited because the concept of ‘classical symmetries’ here is much more rigid that one might like (namely symplectic transformations), thanks to the requirement that they act on all the extra data we need for geometric quantization. Still, it’s a principled way to get the angular momentum operators on the spin-j representation of SU(2), or more generally self-adjoint operators on representations of a compact simple Lie group coming from Lie algebra elements once you’ve chosen an integral coadjoint orbit (which is more or less the example you mentioned).
More precisely, what bothers me is that if you geometrically quantize a random symplectic manifold with no symmetries, then you don’t have operators. The only operators available seem to be the ones coming from symmetries, and if you are going to stick to systems with symmetries you end up looking at co-adjoint orbits. These lie in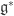
and you end up in the orbit method context I was trying to advertise (for much much more about this context, see the collected works of David Vogan…)
For a space of functions S on a phase space P, with addition, multiplication and Poisson bracket as three binary operations, the latter two being both bilinear and the last being a biderivation, we can construct unary operators as actions on the function space,![\hat Y_A(B)=A\cdot B, \hat Z_A(B)=[A,B]](https://s0.wp.com/latex.php?latex=%5Chat+Y_A%28B%29%3DA%5Ccdot+B%2C+%5Chat+Z_A%28B%29%3D%5BA%2CB%5D&bg=ffffff&fg=333333&s=0&c=20201002)
, with the abstract Lie algebra being ![[\hat Y_A,\hat Y_B]=0, [\hat Z_A,\hat Y_B]=\hat Y_{[A,B]}, [\hat Z_A,\hat Z_B]=\hat Z_{[A,B]}](https://s0.wp.com/latex.php?latex=%5B%5Chat+Y_A%2C%5Chat+Y_B%5D%3D0%2C+%5B%5Chat+Z_A%2C%5Chat+Y_B%5D%3D%5Chat+Y_%7B%5BA%2CB%5D%7D%2C+%5B%5Chat+Z_A%2C%5Chat+Z_B%5D%3D%5Chat+Z_%7B%5BA%2CB%5D%7D&bg=ffffff&fg=333333&s=0&c=20201002)
. If we construct a Liouville state, that induces a state over that algebra, which allows us to use the GNS-construction of a representation of the algebra over a Hilbert space.
The difficulties then are that the Liouville operator that generates time evolution is not positive, which the Correspondence Principle requires, and there is no complex structure. For a field theory on Minkowski space we can appropriate the complex structure associated with fourier transform and for the EM field there’s also the Hodge dual, so the field theory case is easier. The correspondence Principle, in contrast, is not absolutely essential, it’s a rule of thumb: we have a Hilbert space (which for fields is complex) we can use for physical models and we have a noncommutative algebra of observables. More than that, the algebraic structures for a free random and quantum field are isomorphic (except that the Liouville operator doesn’t map to the QFT’s Hamiltonian operator).
For how I think this works out in as much detail as I can currently muster, one might look at the 1709.06711 that I mention in my earlier comment below, even though the math is not as pretty as you guys throw about. It will be nice enough if John rehearses all of geometric quantization, doubtless beautifully done as always, but I think he’ll get to where geometric quantization is, and then stop for the next 50 years: a principled detour is needed.
Peter wrote:
I’ll nitpick on two fronts here. First, one of the big lessons of geometric quantization is that a symplectic manifold is not enough to quantize and get a Hilbert space: you need extra structure, like a polarization at the very least (and usually more). Second, why should you get operators if you don’t have symmetries? The lesson of Noether’s theorem, as I see it, is that in physics observables correspond to one-parameter groups of symmetries. I expanded on this here:
• Getting to the bottom of Noether’s theorem.
So, in classical mechanics we expect to get observables from one-parameter groups of symplectomorphisms (though there are cohomological obstructions!), and in geometric quantization we should expect to get observables from one-parameter groups of symplectomorphisms preserving the polarization and whatever other structure we need to do geometric quantization (though again there are obstructions). We can sometimes do better, but I no longer think we have any ‘right’ to.
Naive question: could quantization be a monad, coming from and adjunction between classical and quantum systems? What you described about the relationship between quantum systems and classical systems sounds vaguely like a forgetful functor.
Joe wrote:
Darn, I didn’t think my secret intentions were so transparent. In 2008 I wrote a draft of a paper trying to prove there is such an adjunction. The fact that we get an idempotent monad would then come from the fact that quantum systems are a reflective subcategory of classical ones.
(My go-to example for a reflective subcategory is abelian groups as a subcategory of groups; the left adjoint of the forgetful functor from abelian groups to groups is ‘abelianization’. If we abelianize a group, forget we’ve done so, then abelianize again, it’s just the same as abelianizing just once. Quantization is like that.)
I was writing this paper with a coauthor, who shall go unnamed, who seemed to think all this stuff was not quite worthy of publication. So, I let it slide. Now that we’ve let the cat out of the bag, I should probably finish this paper rather quickly and slap it on the arXiv.
(Hmm, looking at it I see another reason I let it slide: there are some tricky technical issues that need to be resolved.)
Really interesting insights. I really would like to read a series of articles on Geometric quantization from you!
Thanks! Me too! This is the first of a series: now I just have to write the next one.
Dear John, before you write the next post I hope you might try my arXiv:1709.06711, with a title that resonates more than a little with what you say above, “Classical states, quantum field measurement” [for a significantly better version, particularly because it makes a connection with Quantum Non-Demolition measurement after I had a conversation with Carlton Caves and because it is as currently submitted to Physica Scripta (but not yet posted as a v5 to arXiv), go to https://www.dropbox.com/s/xoj3gt81h2fonmf/1709.06711-asSubmittedTo-PhysicaScripta.pdf?dl=0; see, particularly, the Tsang&Caves reference.]
I don’t mention geometric quantization in that paper, except as a reference to Woodhouse, because in my opinion that approach took a wrong turn when it insisted, as why would it not, on the Correspondence Principle, because the Liouville operator in a QND approach is not positive-definite whereas the Hamiltonian operator that generates evolutions in QM/QFT is positive definite (at least, I think that’s the most straightforward way to state the disconnect). If one doesn’t insist on the CP (although there are significant interpretational costs to that!), then isomorphisms are possible not only between the state spaces but also between the operator algebras of quantized EM and of a random field EM (because classical physics is not commutative). It’s important to do this work in the QFT context, IMO, and indeed it’s easier because complex structures are needed and available.
You don’t mention Koopman-von Neumann approaches to classical mechanics above, which I suggest you will want to. It’s kinda fun that that goes back to 1931. There were a few articles about KvN before 2000, but there has been a slow burn of articles about KvN since then, and there’s even a Wikipedia page (nothing to do with me), which I would hope the Baez effect will make a little better known.
You will see that I’m not a terrible mathematician, but also definitely not the best. I ask you please to cut me some slack for that.
Huh. Was my comment lost? It doesn’t say it’s being held back as spam.
Sorry, it was in my spam for some reason. Do you think my blog sends out notifications to people it thinks are spammers? I doubt it.
No indeed! You’ll either like the paper or parts of it or not, but, as you see, whether you like it or not, I’m pretty invested in this. I was miserable, not necessarily thinking straight. Now I’m OK. Sorry^Sorry^Sorry!
Two things. You don’t mention what happens if you geometrically quantize
to 
, then un-quantize to 
; the answer is, there is an inclusion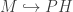 
such that 
spans 
, in the sense that the smallest (projective-)linear subspace of 
containing 
is 
itself.
Secondly, this being more to Peter, the deformation quantization of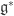
is 
, and to this day I’ve never seen someone clearly state (1) what geometric quantization of a (non-symplectic) Poisson variety is supposed to be (2) how the geometric and deformation quantization pictures are supposed to relate.
Kostant’s geometric quantization picture starts from
and says, pick a line bundle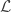 
with (Hermitian) connection 
with curvature 
(where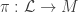 
is the bundle map). The “quantization condition” is the existence of such a line bundle (i.e. whether the symplectic form 
has integral periods). It says nothing about 
being nondegenerate. Note that this sort of degeneracy, though, is exactly opposite to the degeneracy of a Poisson structure; a symplectic form gives an isomorphism 
, a degenerate symplectic form gives only a rightward map, a Poisson structure gives only a leftward map.
Incidentally the exact sequence
(which comes up in determining whether an action of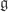
on a symplectic manifold, i.e. Lie algebra map to the Lie algebra 
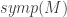of symplectic vector fields) is Hamiltonian)
lifts to a sequence of groups,
though I don’t really know how to think of the cokernel. Indeed, the action of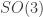
on 
with area 
is generally considered to be Hamiltonian, but only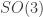 
‘s double cover 
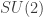acts on the corresponding 
, so shouldn’t be considered Hamiltonian on the group level. But I digress.
Have you seen Cecilia Flori’s Topos QM? It has some very interesting theorems in it.
Hi – no, I haven’t seen this.
Hi Allen,
” I’m not invoking any general theory of how to quantize Poisson manifolds, or any general theory of deformation quantization. The argument is that this is a case where the classical/quantum relationship is completely clear: for operators you get abstractly 
and the appearance of various structures of geometric quantization comes about because of the problem of how to produce irreps of 
by geometric methods from 
.
In saying you should “quantize
You only need deformation quantization if you want a map that takes functions on the classical space to operators. The problems with trying to do that are made very clear here: your function space is the associated graded algebra to the quantum algebra.
Well, it is an example of the general theory of deformation quantization, which as you say deforms the commutative ring
to the noncommutative one 
. I’m still not clear how that’s supposed to relate to geometric quantization.
Categorically, the classical side should be {symplectic manifolds and Lagrangian correspondences}, and the (deformation-)quantum side {noncommutative algebras and bimodules}. One can decategorify the NCAs to their
-groups. Geometric quantization of 
decategorifies to 
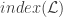i.e. the pushforward to a point in 
-theory of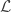 
. I feel like this should be a clue.
(I realize I left out some crucial ingredients in the
-story. One shouldn’t use all modules over the noncommutative algebra, only those in some sort of “category 
“. Then, the 
-group of that module category should match the topological 
-theory of the symplectic manifold. But I don’t understand how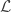 
lives in there, nor how it should be pushed to a point — along the actual map 
, which is not a Lagrangian correspondence.)
Allen wrote:
I plan to spend a lot more time discussing this map
which should be the unit of the adjunction Joe Moeller mentioned. The points in the image of this map are called ‘coherent states’: in some sense they’re the best quantum approximations of classical states. But I hadn’t thought explicitly about how 
spans 
This makes it geometrically vivid how quantization ‘flattens out’ the space of classical states
replacing it by a projective space. (My mental image of projective space is not ‘flat’, but since it’s a kind of enhanced version of affine space we can think of it as flat; in particular we can talk about its projective-linear subspaces.)
One way to say it is that the homogeneous ideal defining the image of
is generated in degree 2 and higher. I wonder if it’s relevant that in the sort-of-semiclassical limit, where one scales the symplectic form by 
and considers 
, that the ideal is actually generated in degree 2, not needing any higher.
We recommend reading of seminal Jean-Marie Souriau papers on Geometric Quantization:
https://projecteuclid.org/euclid.cmp/1103758996
http://www.numdam.org/article/AIHPA_1967__6_4_311_0.pdf
Souriau Works on Geometric Quantization (Prequantization condition, pre-quantum bundle, polarizations, quantification of coadjoint orbits) will be presented and debated at SOURIAU 2019 conference in Paris Denis-Diderot University in May 2019 for 50th birthday of “Structure des systèmes dynamiques” Book:
http://souriau2019.fr/?page_id=40
Click to access the_poster.pdf
“The math is not mysterious here; it’s the physical meaning of the math that’s mysterious. The math seems to be telling us that contrary to what they say in school, quantum systems are special classical systems, with the special property that when you quantize them nothing new happens!”
For only this statement you deserve to be christened as the guru of the physics to come (I am serious).
Wonderful article John, sharp and informative as usual cutting through the fog…
I enjoy very much reading your “Nth quantization” as well as “The square root 2 and the Babylonians”. People should read them.We tend to underestimate the ancients (or overestimate our present knowledge).
Is patience the only price we have to pay to see “the rest of your cards”?
Concerning your “quantum states are not really vectors in a Hilbert space H; from a certain point of view they are really 1-dimensonal subspaces of a Hilbert space”: I find it much more helpful to work with a more abstract point of view, that a state is a normalized real positive linear map over a $\ast$-algebra or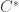
-algebra, then we can use the GNS-construction of a representation of the algebra over a Hilbert space. In particular, this approach levels the playing field for random and quantum fields, pushing the former towards a Koopman-von Neumann-type formalism instead of towards a phase space formalism. I know I’m not teaching you anything by this, but there it is.
The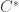
-algebraic approach is good for some things, but I haven’t found it so helpful for project that I’m discussing in this blog article, namely relating geometric quantization and algebraic geometry. I can try to say things in a 
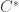-algebraic way, though: the space of pure states on a finite-dimensional 
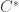-algebra is a Kähler manifold equipped with precisely all the extra structure needed for geometric quantization.
I can see that being a way to go, but in my preferred context of random and quantum fields, the idea of a pure state is too delicate, insofar as a more general space of states would be of integral forms that have infinite refinements: one would have to work with state-valued distributions or something similar, which might get messy. But that obviously doesn’t have to worry you for CM/QM. I look forward to the next installment.
As you probably know, projective Hilbert space is in a natural way the boundary of the space of density matrices.
Yes, that’s cool! I especially like this in the case of the spin-1/2 particle, i.e. the Hilbert space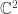
, where the projective Hilbert space 
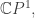usually called the Riemann sphere, is also known in this context as the Bloch sphere, which in turn is the boundary of what should be called the ‘Bloch ball’, the space of 
density matrices. I love how the group of projective transformations of the Riemann sphere is also the Lorentz group for 3+1-dimensional Minkowksi spacetime. And I love how all this generalizes to real, quaternionic and octonionic cases if we go to 1+1, 5+1 or 9+1-dimensional Minkowski spacetime!
•
and Lorentzian geometry.
Some ideas of geometric quantization extend to
and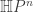 
—and even 
for 
But I digress… this stuff is sort of strange.
John,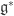
and representation theory, in which case the relation of 
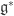and 
gives a simple fundamental point of view on the classical/quantum relationship, one however that starts on the operator side. The geometric quantization of co-adjoint orbits provides the state side of the story. Seems to me the best point of view is to be aware of both sides of the story
I agree with you completely that operators should come from a symplectic group. Accepting that though, my second point was that once you have this group action (and enough operators for it to be transitive), you have a theorem saying your symplectic manifold is a co-adjoint orbit (or a cover of such). So, I’m just pointing out that in this case you’re already placing yourself in the context of the relationship of orbits in
I agree completely. In this series of blog posts I want to develop a rather heterodox line of thought. If I ever gets rolling, I will focus on the geometric quantization of complex projective varieties; the coadjoint orbits of compact Lie groups give very symmetrical examples, with lots of operators coming from symmetries, but there are plenty of other great exawant to talk about.
Note that
acts symplectically and transitively on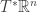 
, and the free loop group 
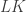acts symplectically and transitively on the based loop group 
, but in neither case is the symplectic manifold a coadjoint orbit of the group — only of a central extension.
Your remark that the quantisation of
is 
itself is only true if you take the symplectic form to have cohomology of degree 1, i.e. be the (
invariant) de Rham representative of the first Chern class of the line bundle of degree 1 aka 
, the dual of canonical sub bundle. For 
if you take the n-fold tensor bundle of the line bundle with itself (for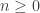 
the space of holomorphic sections becomes 
(note the dualisation!).
The more interesting question is what happens when
. The line bundles 
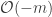don’t have sections but 
where 
.
One way to understand this is to consider the natural
structure on the compact Kähler manifold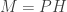 
with (even and odd) spinor bundle 
(for even reps odd 
). The Kernel and cokernel of the Dirac operator on this Spinor bundle are the (even and odd Dolbeault) cohomology groups of the prequantum line bundle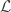 
. Note that a hermitian metric on the 
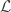gives a (pre) Hilbert space structure on the space of (smooth) sections that depends on the complex structure, but not depend on the metric of M. It just so happens that for 
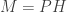only the zeroth or the top cohomology groups are nonzero, but this is not true for Kähler varieties in general.
Rogier wrote:
Right. I’m gearing up to talk about some functors, and one of these sends any finite-dimensional Hilbert space
to the projective space 
equipped with the dual of its canonical line bundle. The tensor powers of this line bundle are also very important but I’d prefer to package those up in another bunch of functors, namely those that take a space (of some suitable sort) with a line bundle and take the 
th tensor power of that line bundle.
I haven’t thought about the case where
is negative and the tricks one must do to get geometric quantization to do something interesting in this case. You and Allen are both saying “Dirac operator”, and someday I’ll have to think about that.
I’m guessing you mean tautological bundle, not canonical bundle. (Yes, the tautological bundle is canonical, but it’s not “the canonical line bundle”. The terminology is very annoying.)
I can never remember the terminology here. The bundle I really like is the bundle of lines over projective space where the line over each point is the line that is that point. Actually I like the dual of this even better, since that’s the one that has global sections.
Yeah I messed that up.
Every complex manifold
has a canonical line bundle which is 
. It figures prominently in Serre duality. Only the projective spaces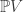 
have a tautological line bundle 
which at a line ![[x]](https://s0.wp.com/latex.php?latex=%5Bx%5D&bg=ffffff&fg=333333&s=0&c=20201002)
is the line itself and a tautological quotient bundle 
. Same holds true for the Grassmannians except of course that for a Grassmann 
is just a line bundle, but a sub bundle.
Just checking: given a complex submanifold of projective space,
, is the canonical line bundle of 
(naturally) isomorphic to the restriction to 
of the dual of the tautological line bundle on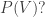 
The tautological bundle absolutely does not restrict to the canonical bundle (except in special cases). In fact this is already wrong for P^n. For P^n he canonical bundle is K = O(-n -1). This is easy to see, as c_1(K) = c_1(T^* P^n) = -c_1(TP^n) and TP^n = Hom(S, Q) = Q(1) sits in the exact sequence
0 –> O –> C^{n+1}(1) –> Q(1) –> 0.
For a complete intersection M of degree d_1, d_2,…d_m in P^n the canonical bundle is O(\sum_i d_i – n -1) restricted to M. This follows from the adjunction formula which just follows by induction and noting that the normal bundle of the smooth zero of a polynomial of degree d is O(d) restricted to the zero. It shows in particular that not all projective varieties are complete intersections as there exist varieties with K^{\dim(M)} = 0.
(written in “asci art Tex” as I keep messing things up the latex/jax thingy).
.
Rogier wrote:
I tried to fix your typos; I’m always happy to do that; but I’m confused about this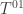
thing—is that a typo or some bundle I don’t know about? I also don’t understand “even reps odd 
“. I guess I don’t understand this particular math well enough to figure out what is or is not a typo!
Thanks for fixing up!
No it is not a typo.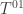
is the anti linear cotangent bundle whose (smooth) sections 
are, in a local complex neighbourhood, of the form
. The vector bundle 
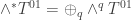has as sections 
i.e. all forms that are locally sums of q wedges of 
‘s. This obviously splits up in a space of even and odd forms which are the even and odd spinors respectively.
This is the standard way to give a complex manifold a base
structure which you can twist with line bundles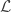 
by tensoring to get every other 
structure (in other words, the 
structures are a torsor under 
). For a holomorphic linebundle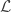 
the Dirac operator on this Spinor bundle is just 
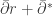. For Kähler manifolds, the Kähler identities allow you to identify the kernel and cokernel of the Dirac operator with the even respectively odd Dolbeault cohomologies 
.
Note, however, that the
structure and the Dirac operator make perfect sense if you only have an almost complex structure. If you go from the almost complex structure to its complex conjugate one, everything gets dualised! The 
structure corresponding to a line bundle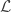 
in one structure corresponds to 
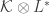in the other, where 
is the canonical line bundle.
Argh.
s/\dual/*/
s/\bar\partial r/\bar\partial
This offers me plenty to think about. For now I’ll just mention that 1) your main LaTeX typos are using the nonexistent commands \tensor and \dual and writing \matcal for \mathcal, but 2) I don’t mind fixing mistakes, since it gives me an excuse to really think about what you’re saying.
One more remark. Every symplectic manifold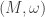
is almost complex in a natural way, i.e. uniquely up to homotopy.
To see this, choose a Riemannian metric
. This is a contractible set of choices and so harmless up to homotopy. Write the symplectic form as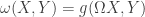 
for a uniquely defined 
. Then 
so that 
. Hence 
is positive semi definite. In fact 
is positive definite because 
is non degenerate. Now define (e.g. using the functional calculus) 
. Since everything in sight commutes, you see that 
, and you have cooked yourself an almost complex structure.
I can follow the math above, just about, but I hope some time might be given to considering what the relationship between classical and quantum might be in broader and more concretely accessible terms and to characterizing that relationship more independently of the obvious historical importance of the process of quantization.
Much time is spent, I would say not very productively, proving that quantum is different from classical, because of the violation of the Bell inequalities, Gleason’s theorem, et cetera, and yet these results rest only on the algebra of operators being noncommutative (for the Bell case for C*-algebras, there’s /Landau PhysLettA 1987/, which is significant for working without reference to nonlocality, important though nonlocality is, and one might prefer /Baez LettMathPhys 1987/, which is quite similar). Classical physics fully construed, including what I think has to be called a sophisticated understanding of the Poisson bracket even though it is a commonplace here, does include a noncommutative algebra of operators, so that none of these differences are pertinent to understanding the difference between classical and quantum.
OTOH, quantum theory includes a complex structure that can only be introduced by fiat in classical mechanics, by introducing a Kähler manifold or some similar structure. However, for the EM field there are two natural complex structures, due to the Hodge dual and to the sine and cosine fourier transforms associated with the translation group, so that even this difference is not relevant for the physically significant case of the EM field. Reducing the measurement theory and state spaces of quantum fields to be the same as those of classical random fields perhaps makes the classical case weirder more than it simplifies the quantum case, but still it seems to me to help to unify the two (again, independently of any quantization process).
Finally, quantum computation is about isolating a (finite) N-dimensional Hilbert space from interactions with the rest of the world and implementing specific unitary evolutions and generalized measurements applied to that Hilbert space. But if noncommutative algebras of operators, Liouville states over that algebra, and the Hilbert spaces that we can GNS-construct from that structure are a natural formalism for classical physics, how does that differ from classical analog computation, except only in finite dimensionality? It’s commonplace to dismiss analog computation as of a different kind to quantum computation, but not to characterize with any sophistication what that difference is. Quantum computation will only be very fractionally less difficult to engineer if we understand the conceptual relationship more precisely, but again it seems to me to help.
I suppose I have to expect this comment will be ignored, and I apologize if it seems too mathematically unrefined for here, and too long, but I live in reckless hope.
Sorry, I don’t have time to write about broader issues, or explain known material. It’s too bad you didn’t join the conversation on sci.physics.research back in the late 80’s or 90’s—back then I was thinking about quantum gravity full time, and I spent endless hours discussing quantization methods, the philosophy of quantum mechanics, quantum field theory and the like. These days I’m mainly working on category theory applied to macroscopic classical systems. I just happen to have a few thoughts on the mathematics of geometric quantization. They’ve been simmering on the back burner for about a decade, and I feel it’s time to start talking about them and developing them in more detail. So that’s what this series is about, and that’s all it’s about.
I’m only aiming it to be readable by people who already know and love the usual story of geometric quantization. For that, you might like this summary of an old sci.physics.research discussion, or the discussion itself:
• John Baez, Geometric quantization.
Unfortunately this doesn’t dig too far into the geometric quantization of Kähler manifolds, which is my main interest now. For that I recommend these:
• Matthias Blau, Symplectic geometry and geometric quantization.
• A. Echeverria-Enriquez, M.C. Munoz-Lecanda, N. Roman-Roy, C. Victoria-Monge, Mathematical foundations of geometric quantization.
For more detail:
• N. M. J. Woodhouse, Geometric Quantization, Oxford U. Press, 1997.
Right. In the best cases there’s a unique Kähler structure with your existing symplectic structure as its imaginary part that’s invariant under some symmetry group you happen to like and has some other nice properties.
For example: the normalizable real solutions of the vacuum Maxwell equations have a well-known Poincaré-invariant symplectic structure. This extends to a unique complex inner product that’s Poincaré-invariant.
(And of course, a complex Hilbert space is a nice example of an infinite-dimensional Kähler manifold. The Bargmann–Segal approach to second quantization can be seen as geometric quantization applied to a Hilbert space.)
The link above to “Symplectic geometry and geometric quantization” appears to be broken; the one on the nLab points here.
Thanks! I’d taken Blau’s Postscript file, converted it to PDF, put it on my website, and given the wrong link. But I’ll take advantage of this mistake to point to the nLab version instead.
Many thanks, John, and thanks also, Blake, for the corrected link. AFAICT, both the Blau and the math-ph/9904008 perpetuate the idea that the classical observables are only functions on phase space, discounting that one can as much ask in classical physics as one can in quantum physics whether a state is an eigenstate of a unary transformation operator (such as a rotation that is generated by the biderivational Poisson bracket). Keeping it simple, in the absence of constraints, with a trivial symplectic form, classical operators include all functions
, which, given also a Liouville state over this operator algebra, allows us to GNS-construct a (real or complex) Hilbert space, from which observables would presumably be, as usual, self-adjoint or normal operators, to taste. I’m glad to be even more clear that my approach to this is not geometric quantization: it is, so to speak, Koopman-von Neumann-ization, so given that John wants to discuss only geometric quantization, if anyone wishes to follow my gravatar link to my Facebook page and comment there, I will be there and as welcoming as I can, but in any case I’m sorry that I misunderstood some of the comments in the OP to be closer to my approach than I had thought.
So, next time I’ll present a simplified version of geometric quantization, where we throw out most of these structures and keep only enough to get a complex vector space, not a complex Hilbert space. In fact I’ll throw out the symplectic and Riemannian structures on our manifold M and only keep the complex structure! This is pretty heretical from the viewpoint of physics, but in fact it’s quite standard in mathematics. Indeed, I don’t want to get your hopes up too much: if you know some algebraic geometry, you should find most of what I say quite familiar. But I think this is a good way to get started on setting up a pair of adjoint functors: ‘quantization’ and the reverse process I mentioned last time: ‘projectivization’.
This sounds complicated! Luckily, when you unravel it all you get a much simpler description, pointed out by Allen Knutson in a comment to Part 1. Namely, given our variety
there’s a smallest subspace 
such that 
sits inside the projective space 
We have
This simpler description makes it blatantly obvious that
So,
is a functor.
[…] John Baez has a popular article at Nautilus about his new-found love for algebraic geometry, as an explanation of the relation of classical and quantum. The more technical version is a series of posts here. […]
[…] Groenewold’s theorem on the inconsistency of canonical quantization and John Baez’s article series on some modern approaches). In our case, however, the recipe is simple: turn the kinetic energy […]
Does the second quantization functor have a fixed point?
The concept of “fixed point” needs to be handled carefully when you have a functor instead of a function. In one sense any algebra of any monad counts as a “lax fixed point” of that monad. But there’s a lot to say about this.