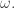Geometric quantization is often presented as a way to take a symplectic manifold and construct a Hilbert space, but in fact that’s a better description of ‘prequantization’, which is just the first step in geometric quantization. Even that’s not completely accurate: we need to equip our symplectic manifold with a bit of extra structure just to prequantize it. But more importantly, when we do this, the resulting ‘prequantum Hilbert space’ is too big: we need to chop it down significantly to get a Hilbert space suitable for the quantum description of our physical system. And to chop it down, we need to equip our symplectic manifold with a lot more extra structure. So much extra structure, in fact, that the whole idea of ‘quantizing a symplectic manifold’ starts sounding more like the wistful, nostalgic description of a naive hope than an honest account of what we’re really doing.
So, it’s probably better to admit that ‘quantizing a classical system’ is not a real thing. More precisely—because people will rightly object to that over-bold statement—there’s no systematic procedure that takes us all the way from the mathematical structures used to describe a large class of classical systems to those used to describe quantum systems, with no further inputs required. Sure, we can make quantization more systematic by limiting the class of systems it’s supposed to handle. We can also make it more systematic by having it do less: for example, just prequantization instead of full-fledged quantization. Both those options have been explored for many decades. Let’s instead try something new.
For starters, let’s accept the fact that the world was not created classically by God on the first day and quantized on the second.
The world is quantum; under some conditions it looks approximately classical. So instead of treating the lack of a purely functorial quantization procedure for symplectic manifolds as a failure, let’s accept it and try some new ways of thinking about the meaning of geometric quantization.
To make things specific, let’s consider Kähler quantization. Here we start not with a raw symplectic manifold, but much more. For starters, we take a Kähler manifold, which is a smooth manifold equipped with a beautiful trio of structures:
1) a symplectic structure
2) a complex structure
3) a Riemannian metric
fitting together in a way that obeys this equation:
whenever we have two tangent vectors at any point of
This equation says how any two of
are enough to determine the third.
Each tangent space of a Kähler manifold is a complex Hilbert space—which is downright suspicious, given that in quantization we’re aiming to get a complex Hilbert space. Here’s how it works:
1) the symplectic structure gives the imaginary part of the inner product on each tangent space of
2) the complex structure gives the operation of multiplication by
on each tangent space, and
3) the Riemannian metric gives the real part of the inner product on each tangent space.
The equation
says that the imaginary part of the inner product of and
equals the real part of the inner product of
and
In particular, each finite-dimensional Hilbert space is a Kähler manifold. Similarly, an infinite-dimensional Hilbert space is a kind of infinite-dimensional Kähler manifold.
So, you can think of a complex Hilbert space as a special kind of Kähler manifold: a flat and simply-connected one. Or—less precisely but quite evocatively—you can think of a Kähler manifold as a curved generalization of a complex Hilbert space!
If Kähler quantization were a systematic procedure for extracting a Hilbert space from a Kähler manifold, these facts would lead us to a clear view of what this procedure is doing. Namely, it’s taking a general Kähler manifold and ‘flattening it out’ in a very clever way, producing a Hilbert space. Perhaps a better word than ‘flattening’ would be ‘linearizing’, since this emphasizes the all-important linearity built into quantum mechanics.
Something like this is true—but it can’t be the whole story, because Kähler quantization requires more input than a mere Kähler manifold to produce a Hilbert space! We also need a complex line bundle over our manifold
Vectors in our Hilbert space will not be just complex-valued functions on
rather, they will be (nice) sections of this line bundle.
It would be nice to understand this in a deeply physical way. For example, we might try to insist that the ‘true’ space of classical states is not the manifold but something with one extra dimension built from this line bundle
This thing is not a symplectic manifold: it’s called a contact manifold. Fans of contact geometry will argue, quite convincingly, that the ‘phases’ so important in quantum mechanics are already lurking in classical mechanics, invisible when we use symplectic manifolds, but evident when we use contact manifolds! If we take this seriously, maybe we shouldn’t be trying to geometrically quantize symplectic manifolds in the first place: maybe we should be using contact manifolds.
However, even taking our Kähler manifold and this complex line bundle
over it as input is not enough to systematically construct the long-sought Hilbert space. We need more!
1) We need to equip with a connection whose curvature is
This is our way of making
compatible with the symplectic structure on
We need this even for prequantization: it lets us turn smooth functions on
(‘classical observables’) into operators on the space of sections of
(‘quantum observables’).
2) We need to equip with the structure of a holomorphic line bundle. This is our way of making
compatible with the complex structure on
We need this to cut down the big vector space obtained in prequantization to a smaller one: the space of holomorphic sections of
3) We need to equip with the structure of a hermitian line bundle. I would like to say this is our way of making
compatible with the Riemannian structure on
since that would make everything very symmetrical—but it doesn’t seem correct! Instead, we need this to put an inner product on the space of holomorphic sections of
so we can get a Hilbert space.
All this must sound like a real slag-heap of mathematics, if you’re not already in love with it! It’s beautiful when you get to know it, especially when you look at examples. But I find it difficult to motivate everything on physical grounds, and I also find it a bit difficult to keep track of all these interacting structures.
So, next time I’ll present a simplified version of geometric quantization, where we throw out most of these structures and keep only enough to get a complex vector space, not a complex Hilbert space. In fact I’ll throw out the symplectic and Riemannian structures on our manifold and only keep the complex structure! This is pretty heretical from the viewpoint of physics, but in fact it’s quite standard in mathematics. Indeed, I don’t want to get your hopes up too much: if you know some algebraic geometry, you should find most of what I say quite familiar. But I think this is a good way to get started on setting up a pair of adjoint functors: ‘quantization’ and the reverse process I mentioned last time: ‘projectivization’.
A question
Since I’ve got your ear, let me ask a question. Suppose we have a holomorphic hermitian line bundle on a Kähler manifold
. I can think of three ways in which a connection
on
can be compatible with all this structure:
1) We can demand that the curvature of the connection equal
2) We can demand that the connection be compatible with the holomorphic structure of
Let me spell this out a little. Since
is a holomorphic line bundle there’s a
operator that we can apply to any section of
and get an
-valued 1-form. This is an
-valued (0,1)-form, meaning that written out in holomorphic complex coordinates
it has
terms but no
terms. On the other had, we can use the connection
to take the covariant derivative of
which is a
-valued 1-form
and take its (0,1) part, denoted
Then, we can demand that these agree:
3) We can demand that the connection be hermitian. This means that the directional derivative of the inner product of two sections of
can be computed using a kind of product rule where we differentiate each section using
Namely:
for any vector field on
and any sections
of
I’m confused by when we can find a connection obeying all three of these conditions. Here are some things I know.
First, any holomorphic hermitian line bundle has a unique connection obeying 2) and 3). This is called the Chern connection and its construction is actually given here:
• Wikipedia, Hermitian metrics on a holomorphic vector bundle.
Does this connection also obey 1)? I see no reason why, in general: condition 1) involves the symplectic structure on while conditions 2) and 3) don’t mention the symplectic or Riemannian structure on
just its complex structure.
Second, we can find a connection obeying 1) iff represents, in de Rham cohomology, the Chern class of the line bundle
If
is an integral 2-form we can always find some line bundle
for which this is true.
Can we find a holomorphic line bundle for which this is true? Can we then choose a holomorphic connection on this line bundle obeying 1)? If I understood Picard groups better, I might know.
But as you can see, my understanding of how conditions 1)-3) interact is rather weak. I feel I should have seen this spelled out carefully in a book on geometric quantization—but I don’t think I have.
• Part 1: the mystery of geometric quantization: how a quantum state space is a special sort of classical state space.
• Part 2: the structures besides a mere symplectic manifold that are used in geometric quantization.
• Part 3: geometric quantization as a functor with a right adjoint, ‘projectivization’, making quantum state spaces into a reflective subcategory of classical ones.
• Part 4: making geometric quantization into a monoidal functor.
• Part 5: the simplest example of geometric quantization: the spin-1/2 particle.
• Part 6: quantizing the spin-3/2 particle using the twisted cubic; coherent states via the adjunction between quantization and projectivization.
• Part 7: the Veronese embedding as a method of ‘cloning’ a classical system, and taking the symmetric tensor powers of a Hilbert space as the corresponding method of cloning a quantum system.
• Part 8: cloning a system as changing the value of Planck’s constant.


The phrase you are seeking is a Hodge manifold.
I wasn’t seeking that phrase, but thanks very much: it turns out I was seeking the Kodaira embedding theorem, which is what you linked to! This is exactly the hole in my education that I was trying to fill.
For those too lazy to look, here’s the idea. Someone please correct me if this is wrong, or add related results if I’m missing something good.
Suppose we have a compact complex manifold equipped with a holomorphic complex line bundle
equipped with a holomorphic complex line bundle  Given any hermitian metric on
Given any hermitian metric on 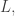 this bundle has a unique connection
this bundle has a unique connection  called the Chern connection with the properties sketched in my article. The curvature of this connection is a (1,1)-form; let’s call it
called the Chern connection with the properties sketched in my article. The curvature of this connection is a (1,1)-form; let’s call it 
We say is positive if there exist a hermitian metric on it such that
is positive if there exist a hermitian metric on it such that
is the imaginary part of a Kähler structure on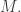 This is equivalent to demanding that
This is equivalent to demanding that
for every nonzero tangent vector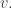
The Kodaira embedding theorem says that if is positive then
is positive then  can be embedded as a submanifold of
can be embedded as a submanifold of  for some sufficiently large
for some sufficiently large  in such a way that for some sufficiently large
in such a way that for some sufficiently large 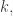
 is isomorphic to the pullback of the dual of the tautological line bundle over
is isomorphic to the pullback of the dual of the tautological line bundle over 
In fact it says more because it actually exhibits this embedding, but I’m too lazy to explain that now.
We can go further using Chow’s theorem: actually embeds as a projective variety in
actually embeds as a projective variety in 
We can say all this a bit differently if we start with a compact Kähler manifold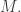 Then the imaginary part of the Kähler structure is a (1,1)-form
Then the imaginary part of the Kähler structure is a (1,1)-form 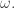 We say
We say  is integral if it represents an integral element of deRham cohomology.
is integral if it represents an integral element of deRham cohomology.
If is integral we say the Kähler structure on
is integral we say the Kähler structure on  is a Hodge metric and call
is a Hodge metric and call  a Hodge manifold. In this case we can find a hermitian holomorphic line bundle
a Hodge manifold. In this case we can find a hermitian holomorphic line bundle  over
over  whose Chern connection has curvature
whose Chern connection has curvature 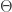 with
with
And so, in this case can be embedded as a projective variety in
can be embedded as a projective variety in  for some sufficiently large
for some sufficiently large  in such a way that for some sufficiently large
in such a way that for some sufficiently large 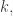
 is isomorphic to the pullback of the dual of the tautological line bundle.
is isomorphic to the pullback of the dual of the tautological line bundle.
So now (aside from the slightly mysterious factor of k), you have a geometrical understanding of the vector space that arises in Kahler quantization.
Yes, I knew that already: what I didn’t know was such an absurdly simple sufficient condition for the prequantum line bundle on a compact Kähler manifold to be ample! That makes everything really nice.
I have a whole schtick about the factor of which I’m gonna drag into this story later.
which I’m gonna drag into this story later.
By the way, nobody should trust Wolfram Mathworld about Kodaira’s embedding theorem. I used to submit corrections for errors in that site, but now I don’t even see where to do that.
http://mathworld.wolfram.com/contact/
“the ‘phases’ so important in quantum mechanics are already lurking in classical mechanics”
Can you say more in a few sentences, or point me at something to read?
Ugh—there really should be a good explanation somewhere, but I don’t know where! If you study enough contact geometry you’ll see this is what’s really going on, but I’m not sure anyone comes out and says it. Someone must have, somewhere: I learned it in conversations.
Briefly, the symplectic structure in classical mechanics is a 2-form on phase space, but locally we have
on phase space, but locally we have  where
where  is a 1-form called the ‘symplectic potential’. For example, for a particle in
is a 1-form called the ‘symplectic potential’. For example, for a particle in 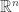 we have
we have
See tautological 1-form for more.
Integrating this 1-form along a path gives the ‘action’ of the path, but if we exponentiate this integral:
along a path gives the ‘action’ of the path, but if we exponentiate this integral:
we get the ‘change in phase’ along the path. We need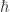 here to make the quantity in the exponent dimensionless! However, all this is still classical mechanics.
here to make the quantity in the exponent dimensionless! However, all this is still classical mechanics.
We can formalize this further by working with a circle bundle over phase space, which becomes a contact manifold when equipped with this 1-form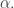 We can think of this circle bundle as the ‘true phase space’ which actually keeps track of the phase of the classical particle, a quantity which is—ironically—forgotten when using the ordinary phase space.
We can think of this circle bundle as the ‘true phase space’ which actually keeps track of the phase of the classical particle, a quantity which is—ironically—forgotten when using the ordinary phase space.
Contact geometry lets us understand how the Hamilton–Jacobi equation describes classical particles as ‘wavefronts’: surfaces of constant action.
Too much to say; sorry. I am writing a book on classical mechanics and you just reminded me that I need to write a few more chapters!
Thanks! I look forward to looking into this further over the break.
You’re writing a book on classical mechanics? Awesome! Keep us updated.
The current draft is here. I’m moving very slowly on it, e.g. right now not at all.
Arnold talked a lot about contact geometry and its connections with classical mechanics, thermodynamics, optics and Hamilton–Jacobi, so it’s probably in there somewhere.
If I understood contact manifolds, I’d probably find the relevant parts in Mathematical methods of classical mechanics appendix 4, “Contact structures”. Other places he talks about contact manifolds are Geometric methods in the theory of ordinary differential equations §8, “The non-linear first-order partial differential equation”; Lectures on partial differential equations lecture 4, “Huygens’ principle in the theory of wave propagation”; and Topological invariants of plane curves and caustics lecture 2, “Symplectic and contact topology of caustics and wave fronts”.
The only problem is, (I’ve read the descriptions in all of these places and still) I don’t understand what contact geometry is supposed to be.
If I look for something “flat” (linear-algebraic) that contact geometry is supposed to be the “curved” (differential-geometric) version of, the best I can do is that it is… a conformal (up-to-scalar-factor) geometry of maximal-rank antisymmetric bilinear forms in odd dimension? Why would anyone want such a thing—in particular, why do we specifically care about “metric” symplectic geometry in the even-dimensional case but “conformal” contact geometry in the odd-dimensional case?
Alex wrote:
Maybe, but I don’t know where. I think the basic ideas are pretty simple, and a lot of what Arnold writes is more complicated.
Symplectic geometry is easiest to understand if you think of it as a generalization of the geometry that any cotangent bundle has—that is, the geometry of position-momentum pairs.
Similarly, contact geometry is easiest to understand if you think of it as a generalization of the geometry that the trivial circle bundle over the cotangent bundle has—that is, the geometry of position-momentum-phase triples. This space is what we really should call “phase space”! Yes, phases are important in classical mechanics too.
I see that I explained this more carefully here 3 years ago.
Hmm, maybe because another motivating example of a contact manifold is the projectivized cotangent bundle. The symplectic structure on the cotangent bundle puts a “nondegenerate 2-form up to an undetermined scale factor” on this.
So, starting from the cotangent bundle there’s a nice way to get a manifold of dimension one more (the circle bundle over it) and and a manifold of dimension one less (its projectivization), both of which are contact manifolds. There’s more about the seccond constructon here, but apparently not the first:
• Wikipedia, Contact geometry: relation with symplectic structures.
They also mention a third: a surface of constant energy in a cotangent bundle can sometimes be made into a contact manifold.
I think it’s time for those of us who write math on WordPress sites to put our heads together and figure out what needs to be done to make WordPress incorporate formulas more gracefully. (This post of yours was especially awkward, with all those short inset formulas. Alas, as you and I and Terry Tao all know, trying to put formulas in-line with dollar-sign latex has its own problems.)
Maybe we should pay someone to create a new WordPress Theme for mathematicians. (I don’t currently have a grant, but I hope to have one again, one of these years!)
I agree that it would be great to make WordPress math look better. Instead of these disgusting small jpegs for equations we could be using MathJax or something even better. Jacques Distler, who just happened by, knows better things, which are used on the nCafé—but I don’t have the technical skills to implement those on a WordPress blog. MathJax has the advantage of being ridiculously easy—I use it on my webpages—but even that, I don’t know how to do on WordPress. Someone must know.
I spent several years trying to support the same technology that you see at the nCafé on WordPress. Eventually, I abandoned the effort because the WordPress codebase was too unbearably crappy to make the cost/benefit worthwhile.
MathJax (which, of course, we use to support browsers without native MathML support) may not be great, but it’s way better than crappy little GIF images.
Okay, here’s how one can use MathJax on WordPress. Can anyone point me to an example of a blog where someone has done this?
I have MathJax set up on my WordPress site (which I host on my own website, rather than on WordPress.com). Here’s an example post with formulae in it.
I don’t have experience with blogs hosted on WordPress.com, but you may be able to add MathJax support by editing the theme’s header file.
You might want to try this https://andrewsun.com/projects/wp-katex/
It’s similar to MathJax, but loads math (supposedly) faster
Furthermore, has a god-given line bundle over it. You see, any point
has a god-given line bundle over it. You see, any point  is really a line in
is really a line in 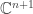 (by which I mean a 1-dimensional subspace), and these lines define a line bundle over
(by which I mean a 1-dimensional subspace), and these lines define a line bundle over  This construction is so ridiculously tautological that people call the resulting bundle the tautological line bundle. This bundle has no holomorphic sections, but its dual has lots: every linear functional on
This construction is so ridiculously tautological that people call the resulting bundle the tautological line bundle. This bundle has no holomorphic sections, but its dual has lots: every linear functional on 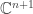 gives one, and that’s how they all arise! I’ll call this dual bundle I’ll call it
gives one, and that’s how they all arise! I’ll call this dual bundle I’ll call it 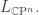 If we restrict
If we restrict  to
to  , we get a holomorphic line bundle with enough sections to be useful in geometric quantization. I’ll call this bundle
, we get a holomorphic line bundle with enough sections to be useful in geometric quantization. I’ll call this bundle 
Even better, and this line bundle
and this line bundle  have the whole laundry list of extra structure and properties that I was bemoaning last time.
have the whole laundry list of extra structure and properties that I was bemoaning last time.
Back here, you mentioned an article of yours. Sorry if this is a dumb question, but which article is that?
Oh, maybe you mean the post we’re commenting under?
Yes. In this article (okay, post) I explained the concept of a Chern connection:
In Part 2 I sketched the usual version of Kähler quantization, which is fairly complicated. Last time I switched to a stripped-down version where these complications are removed… but tried to explain how it was ‘backwards-compatible’ with the usual story, by showing how all the complications could easily be restored if you want them. Unfortunately this makes things look more complicated than they are!
So let me present the same construction again, more cleanly.
To geometrically quantize our symplectic manifold using Kähler quantization, we need to equip it with lots of extra structure, as explained in Part 2. For starters, we need to give it a complex structure. There’s a unique one invariant under rotations, namely the one that makes our sphere into a copy of the Riemann sphere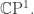 There is then a unique Kähler structure on
There is then a unique Kähler structure on  whose imaginary part is our symplectic structure
whose imaginary part is our symplectic structure